Jun Mei
Every Step Evolves: Scaling Reinforcement Learning for Trillion-Scale Thinking Model
Oct 21, 2025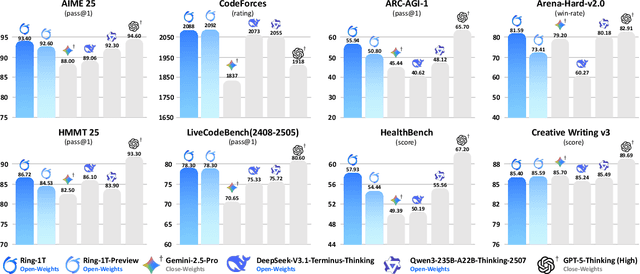
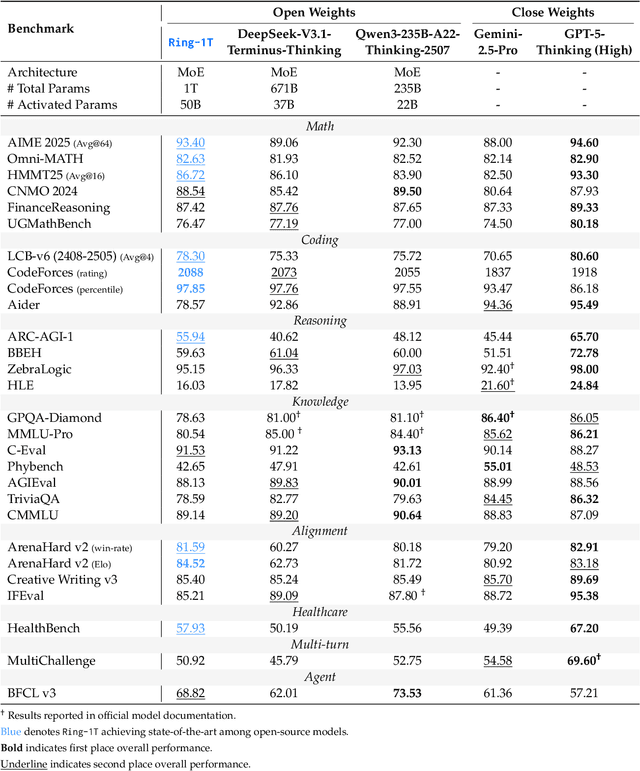
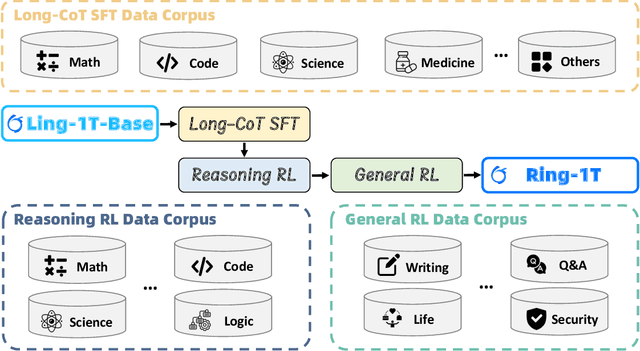
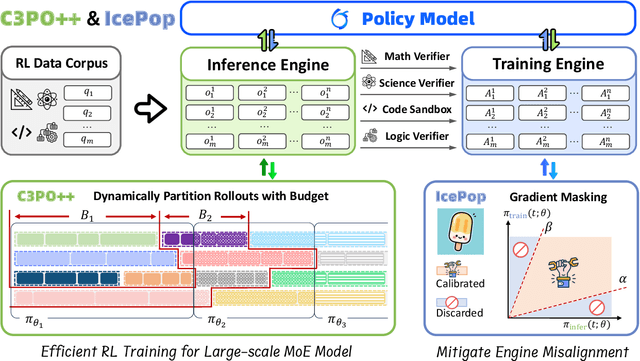
Abstract:We present Ring-1T, the first open-source, state-of-the-art thinking model with a trillion-scale parameter. It features 1 trillion total parameters and activates approximately 50 billion per token. Training such models at a trillion-parameter scale introduces unprecedented challenges, including train-inference misalignment, inefficiencies in rollout processing, and bottlenecks in the RL system. To address these, we pioneer three interconnected innovations: (1) IcePop stabilizes RL training via token-level discrepancy masking and clipping, resolving instability from training-inference mismatches; (2) C3PO++ improves resource utilization for long rollouts under a token budget by dynamically partitioning them, thereby obtaining high time efficiency; and (3) ASystem, a high-performance RL framework designed to overcome the systemic bottlenecks that impede trillion-parameter model training. Ring-1T delivers breakthrough results across critical benchmarks: 93.4 on AIME-2025, 86.72 on HMMT-2025, 2088 on CodeForces, and 55.94 on ARC-AGI-v1. Notably, it attains a silver medal-level result on the IMO-2025, underscoring its exceptional reasoning capabilities. By releasing the complete 1T parameter MoE model to the community, we provide the research community with direct access to cutting-edge reasoning capabilities. This contribution marks a significant milestone in democratizing large-scale reasoning intelligence and establishes a new baseline for open-source model performance.
Ring-lite: Scalable Reasoning via C3PO-Stabilized Reinforcement Learning for LLMs
Jun 18, 2025Abstract:We present Ring-lite, a Mixture-of-Experts (MoE)-based large language model optimized via reinforcement learning (RL) to achieve efficient and robust reasoning capabilities. Built upon the publicly available Ling-lite model, a 16.8 billion parameter model with 2.75 billion activated parameters, our approach matches the performance of state-of-the-art (SOTA) small-scale reasoning models on challenging benchmarks (e.g., AIME, LiveCodeBench, GPQA-Diamond) while activating only one-third of the parameters required by comparable models. To accomplish this, we introduce a joint training pipeline integrating distillation with RL, revealing undocumented challenges in MoE RL training. First, we identify optimization instability during RL training, and we propose Constrained Contextual Computation Policy Optimization(C3PO), a novel approach that enhances training stability and improves computational throughput via algorithm-system co-design methodology. Second, we empirically demonstrate that selecting distillation checkpoints based on entropy loss for RL training, rather than validation metrics, yields superior performance-efficiency trade-offs in subsequent RL training. Finally, we develop a two-stage training paradigm to harmonize multi-domain data integration, addressing domain conflicts that arise in training with mixed dataset. We will release the model, dataset, and code.
AReaL: A Large-Scale Asynchronous Reinforcement Learning System for Language Reasoning
May 30, 2025Abstract:Reinforcement learning (RL) has become a trending paradigm for training large language models (LLMs), particularly for reasoning tasks. Effective RL for LLMs requires massive parallelization and poses an urgent need for efficient training systems. Most existing large-scale RL systems for LLMs are synchronous by alternating generation and training in a batch setting, where the rollouts in each training batch are generated by the same (or latest) model. This stabilizes RL training but suffers from severe system-level inefficiency. Generation must wait until the longest output in the batch is completed before model update, resulting in GPU underutilization. We present AReaL, a \emph{fully asynchronous} RL system that completely decouples generation from training. Rollout workers in AReaL continuously generate new outputs without waiting, while training workers update the model whenever a batch of data is collected. AReaL also incorporates a collection of system-level optimizations, leading to substantially higher GPU utilization. To stabilize RL training, AReaL balances the workload of rollout and training workers to control data staleness, and adopts a staleness-enhanced PPO variant to better handle outdated training samples. Extensive experiments on math and code reasoning benchmarks show that AReaL achieves \textbf{up to 2.57$\times$ training speedup} compared to the best synchronous systems with the same number of GPUs and matched or even improved final performance. The code of AReaL is available at https://github.com/inclusionAI/AReaL/.
Maximum A Posteriori Inference in Sum-Product Networks
Nov 20, 2017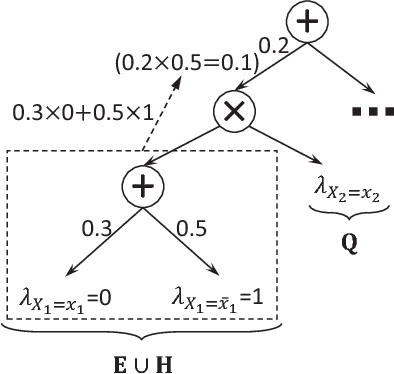
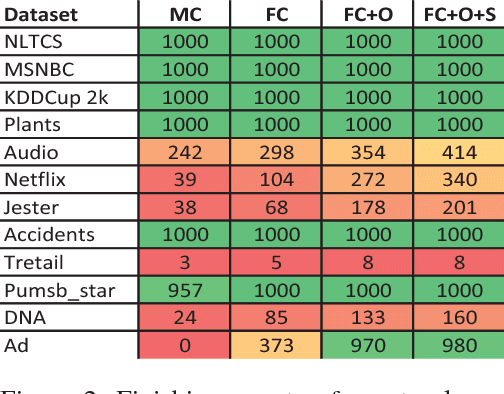
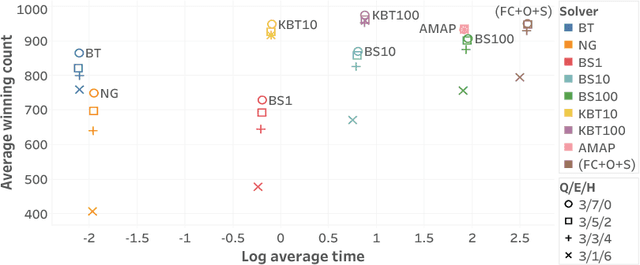
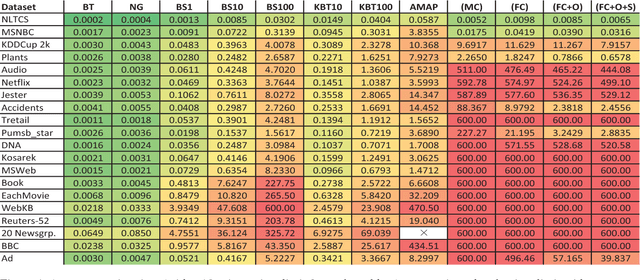
Abstract:Sum-product networks (SPNs) are a class of probabilistic graphical models that allow tractable marginal inference. However, the maximum a posteriori (MAP) inference in SPNs is NP-hard. We investigate MAP inference in SPNs from both theoretical and algorithmic perspectives. For the theoretical part, we reduce general MAP inference to its special case without evidence and hidden variables; we also show that it is NP-hard to approximate the MAP problem to $2^{n^\epsilon}$ for fixed $0 \leq \epsilon < 1$, where $n$ is the input size. For the algorithmic part, we first present an exact MAP solver that runs reasonably fast and could handle SPNs with up to 1k variables and 150k arcs in our experiments. We then present a new approximate MAP solver with a good balance between speed and accuracy, and our comprehensive experiments on real-world datasets show that it has better overall performance than existing approximate solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge