Home and destination attachment: study of cultural integration on Twitter

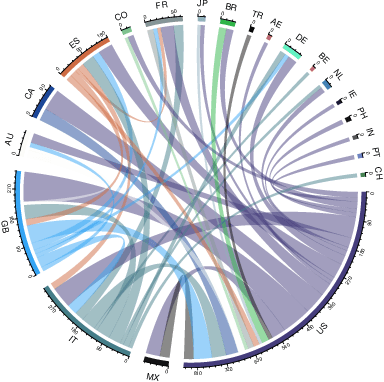
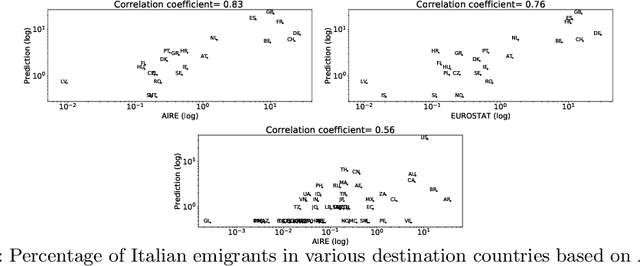
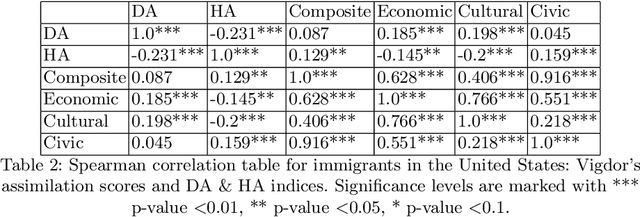
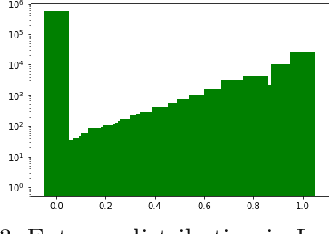
The cultural integration of immigrants conditions their overall socio-economic integration as well as natives' attitudes towards globalisation in general and immigration in particular. At the same time, excessive integration -- or acculturation -- can be detrimental in that it implies forfeiting one's ties to the home country and eventually translates into a loss of diversity (from the viewpoint of host countries) and of global connections (from the viewpoint of both host and home countries). Cultural integration can be described using two dimensions: the preservation of links to the home country and culture, which we call home attachment, and the creation of new links together with the adoption of cultural traits from the new residence country, which we call destination attachment. In this paper we introduce a means to quantify these two aspects based on Twitter data. We build home and destination attachment indexes and analyse their possible determinants (e.g., language proximity, distance between countries), also in relation to Hofstede's cultural dimension scores. The results stress the importance of host language proficiency to explain destination attachment, but also the link between language and home attachment. In particular, the common language between home and destination countries corresponds to increased home attachment, as does low proficiency in the host language. Common geographical borders also seem to increase both home and destination attachment. Regarding cultural dimensions, larger differences among home and destination country in terms of Individualism, Masculinity and Uncertainty appear to correspond to larger destination attachment and lower home attachment.

Generalized Penalty for Circular Coordinate Representation

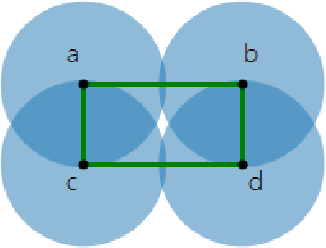
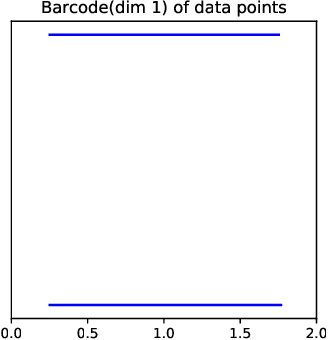
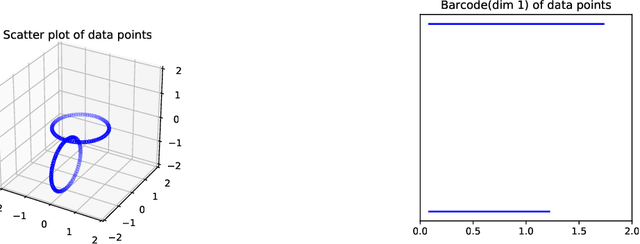
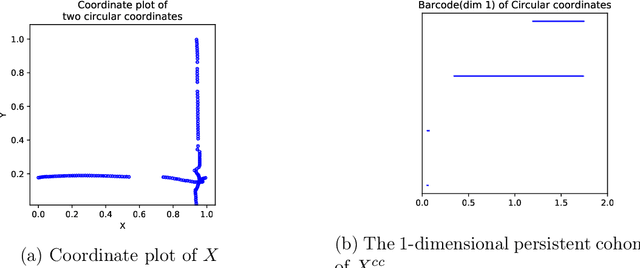
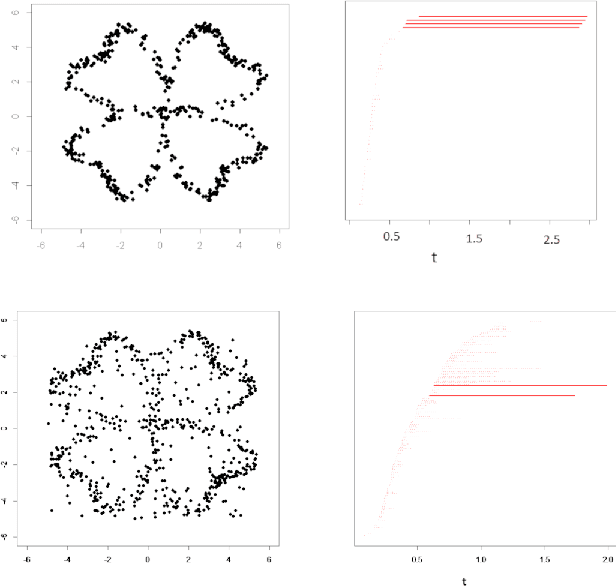
Topological Data Analysis (TDA) provides novel approaches that allow us to analyze the geometrical shapes and topological structures of a dataset. As one important application, TDA can be used for data visualization and dimension reduction. We follow the framework of circular coordinate representation, which allows us to perform dimension reduction and visualization for high-dimensional datasets on a torus using persistent cohomology. In this paper, we propose a method to adapt the circular coordinate framework to take into account sparsity in high-dimensional applications. We use a generalized penalty function instead of an $L_{2}$ penalty in the traditional circular coordinate algorithm. We provide simulation experiments and real data analysis to support our claim that circular coordinates with generalized penalty will accommodate the sparsity in high-dimensional datasets under different sampling schemes while preserving the topological structures.

NTIRE 2020 Challenge on Image Demoireing: Methods and Results

This paper reviews the Challenge on Image Demoireing that was part of the New Trends in Image Restoration and Enhancement (NTIRE) workshop, held in conjunction with CVPR 2020. Demoireing is a difficult task of removing moire patterns from an image to reveal an underlying clean image. The challenge was divided into two tracks. Track 1 targeted the single image demoireing problem, which seeks to remove moire patterns from a single image. Track 2 focused on the burst demoireing problem, where a set of degraded moire images of the same scene were provided as input, with the goal of producing a single demoired image as output. The methods were ranked in terms of their fidelity, measured using the peak signal-to-noise ratio (PSNR) between the ground truth clean images and the restored images produced by the participants' methods. The tracks had 142 and 99 registered participants, respectively, with a total of 14 and 6 submissions in the final testing stage. The entries span the current state-of-the-art in image and burst image demoireing problems.

Efficient Topological Layer based on Persistent Landscapes

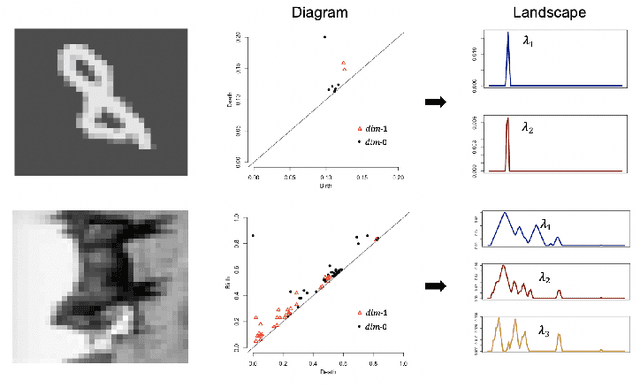
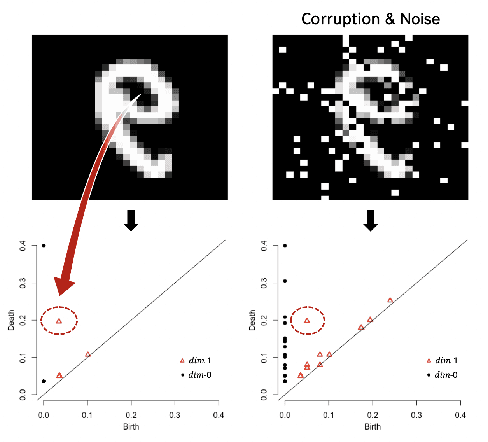
We propose a novel topological layer for general deep learning models based on persistent landscapes, in which we can efficiently exploit underlying topological features of the input data structure. We use the robust DTM function and show differentiability with respect to layer inputs, for a general persistent homology with arbitrary filtration. Thus, our proposed layer can be placed anywhere in the network architecture and feed critical information on the topological features of input data into subsequent layers to improve the learnability of the networks toward a given task. A task-optimal structure of the topological layer is learned during training via backpropagation, without requiring any input featurization or data preprocessing. We provide a tight stability theorem, and show that the proposed layer is robust towards noise and outliers. We demonstrate the effectiveness of our approach by classification experiments on various datasets.

A Penetration Metric for Deforming Tetrahedra using Object Norm

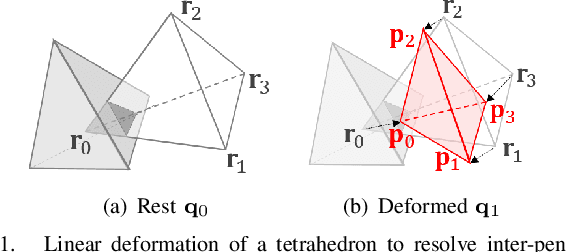
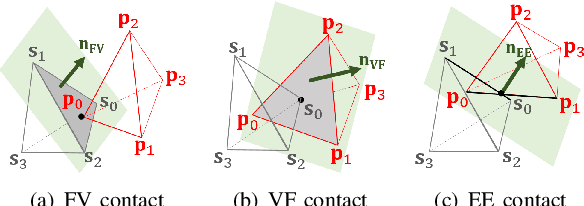
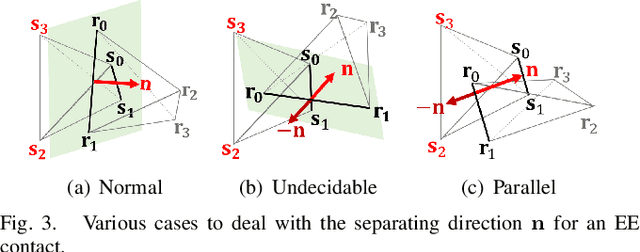
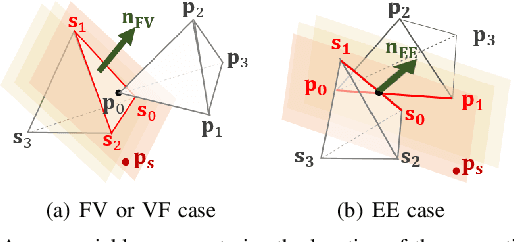
In this paper, we propose a novel penetration metric, called deformable penetration depth PDd, to define a measure of inter-penetration between two linearly deforming tetrahedra using the object norm. First of all, we show that a distance metric for a tetrahedron deforming between two configurations can be found in closed form based on object norm. Then, we show that the PDd between an intersecting pair of static and deforming tetrahedra can be found by solving a quadratic programming (QP) problem in terms of the distance metric with non-penetration constraints. We also show that the PDd between two, intersected, deforming tetrahedra can be found by solving a similar QP problem under some assumption on penetrating directions, and it can be also accelerated by an order of magnitude using pre-calculated penetration direction. We have implemented our algorithm on a standard PC platform using an off-the-shelf QP optimizer, and experimentally show that both the static/deformable and deformable/deformable tetrahedra cases can be solvable in from a few to tens of milliseconds. Finally, we demonstrate that our penetration metric is three-times smaller (or tighter) than the classical, rigid penetration depth metric in our experiments.

Diagnosis of Pediatric Obstructive Sleep Apnea via Face Classification with Persistent Homology and Convolutional Neural Networks

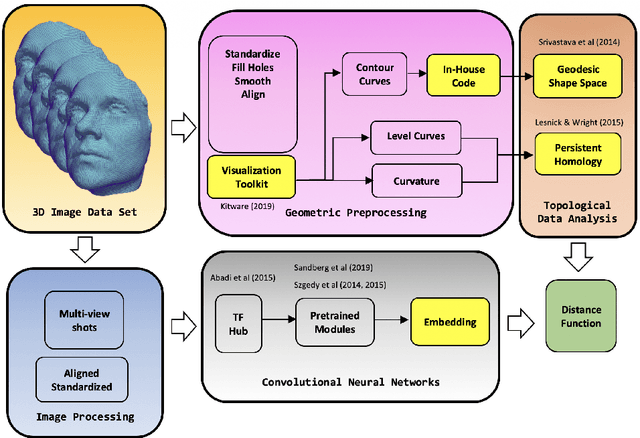
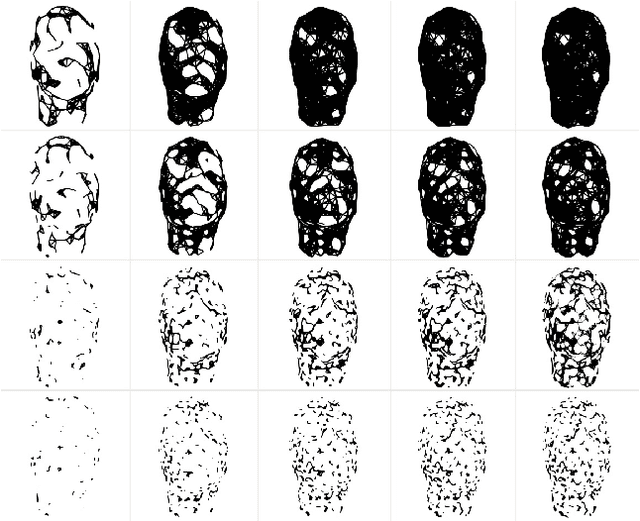
Obstructive sleep apnea is a serious condition causing a litany of health problems especially in the pediatric population. However, this chronic condition can be treated if diagnosis is possible. The gold standard for diagnosis is an overnight sleep study, which is often unobtainable by many potentially suffering from this condition. Hence, we attempt to develop a fast non-invasive diagnostic tool by training a classifier on 2D and 3D facial images of a patient to recognize facial features associated with obstructive sleep apnea. In this comparative study, we consider both persistent homology and geometric shape analysis from the field of computational topology as well as convolutional neural networks, a powerful method from deep learning whose success in image and specifically facial recognition has already been demonstrated by computer scientists.

Time Series Featurization via Topological Data Analysis: an Application to Cryptocurrency Trend Forecasting

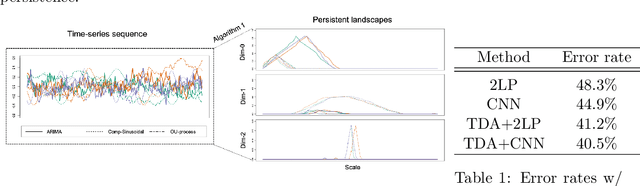
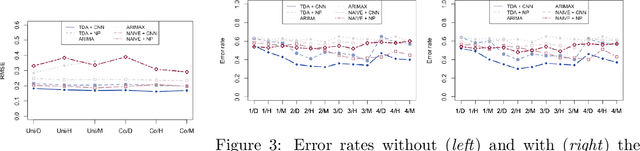
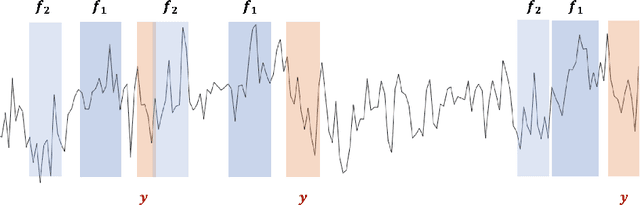
We propose a novel methodology for feature extraction from time series data based on topological data analysis. The proposed procedure applies a dimensionality reduction technique via principal component analysis to the point cloud of the Takens' embedding from the observed time series and then evaluates the persistence landscape and silhouettes based on the corresponding Rips complex. We define a new notion of Rips distance function that is especially suited for persistence homologies built on Rips complexes and prove stability theorems for it. We use these results to demonstrate in turn some stability properties of the topological features extracted using our procedure with respect to additive noise and sampling. We further apply our method to the problem of trend forecasting for cryptocurrency prices, where we manage to achieve significantly lower error rates than more standard, non TDA-based methodologies in complex pattern classification tasks. We expect our method to provide a new insight on feature engineering for granular, noisy time series data.

Causal effects based on distributional distances

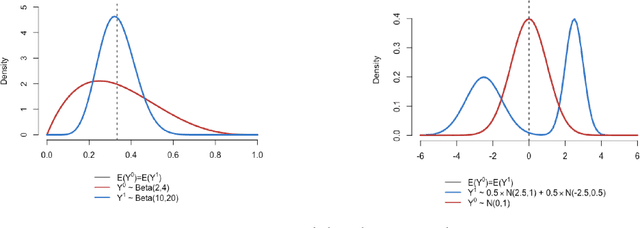
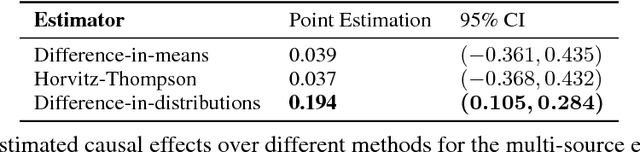
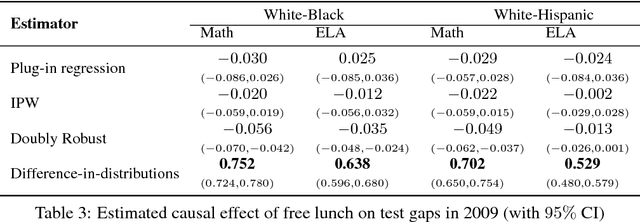
We develop a novel framework for estimating causal effects based on the discrepancy between unobserved counterfactual distributions. In our setting a causal effect is defined in terms of the $L_1$ distance between different counterfactual outcome distributions, rather than a mean difference in outcome values. Directly comparing counterfactual outcome distributions can provide more nuanced and valuable information about causality than a simple comparison of means. We consider single- and multi-source randomized studies, as well as observational studies, and analyze error bounds and asymptotic properties of the proposed estimators. We further propose methods to construct confidence intervals for the unknown mean distribution distance. Finally, we illustrate the new methods and verify their effectiveness in empirical studies.

Statistical Inference for Cluster Trees

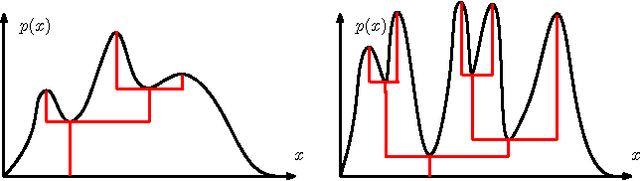
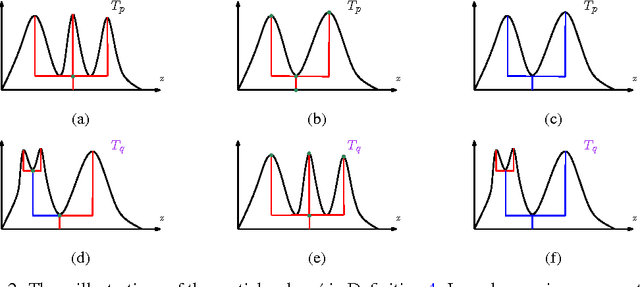
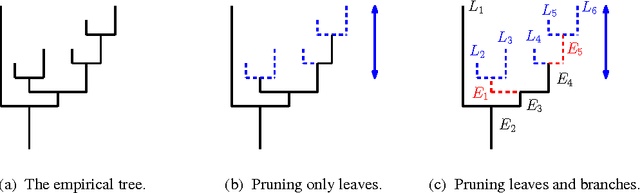
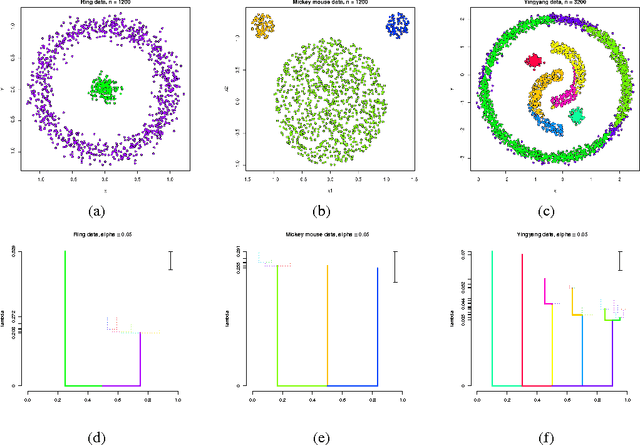
A cluster tree provides a highly-interpretable summary of a density function by representing the hierarchy of its high-density clusters. It is estimated using the empirical tree, which is the cluster tree constructed from a density estimator. This paper addresses the basic question of quantifying our uncertainty by assessing the statistical significance of topological features of an empirical cluster tree. We first study a variety of metrics that can be used to compare different trees, analyze their properties and assess their suitability for inference. We then propose methods to construct and summarize confidence sets for the unknown true cluster tree. We introduce a partial ordering on cluster trees which we use to prune some of the statistically insignificant features of the empirical tree, yielding interpretable and parsimonious cluster trees. Finally, we illustrate the proposed methods on a variety of synthetic examples and furthermore demonstrate their utility in the analysis of a Graft-versus-Host Disease (GvHD) data set.