User Hesitation and Negative Transfer in Multi-Behavior Recommendation

Multi-behavior recommendation aims to integrate users' interactions across various behavior types (e.g., view, favorite, add-to-cart, purchase) to more comprehensively characterize user preferences. However, existing methods lack in-depth modeling when dealing with interactions that generate only auxiliary behaviors without triggering the target behavior. In fact, these weak signals contain rich latent information and can be categorized into two types: (1) positive weak signals-items that have not triggered the target behavior but exhibit frequent auxiliary interactions, reflecting users' hesitation tendencies toward these items; and (2) negative weak signals-auxiliary behaviors that result from misoperations or interaction noise, which deviate from true preferences and may cause negative transfer effects. To more effectively identify and utilize these weak signals, we propose a recommendation framework focused on weak signal learning, termed HNT. Specifically, HNT models weak signal features from two dimensions: positive and negative effects. By learning the characteristics of auxiliary behaviors that lead to target behaviors, HNT identifies similar auxiliary behaviors that did not trigger the target behavior and constructs a hesitation set of related items as weak positive samples to enhance preference modeling, thereby capturing users' latent hesitation intentions. Meanwhile, during auxiliary feature fusion, HNT incorporates latent negative transfer effect modeling to distinguish and suppress interference caused by negative representations through item similarity learning. Experiments on three real-world datasets demonstrate that HNT improves HR@10 and NDCG@10 by 12.57% and 14.37%, respectively, compared to the best baseline methods.

Decentralized Nonconvex Composite Federated Learning with Gradient Tracking and Momentum

Decentralized Federated Learning (DFL) eliminates the reliance on the server-client architecture inherent in traditional federated learning, attracting significant research interest in recent years. Simultaneously, the objective functions in machine learning tasks are often nonconvex and frequently incorporate additional, potentially nonsmooth regularization terms to satisfy practical requirements, thereby forming nonconvex composite optimization problems. Employing DFL methods to solve such general optimization problems leads to the formulation of Decentralized Nonconvex Composite Federated Learning (DNCFL), a topic that remains largely underexplored. In this paper, we propose a novel DNCFL algorithm, termed \bf{DEPOSITUM}. Built upon proximal stochastic gradient tracking, DEPOSITUM mitigates the impact of data heterogeneity by enabling clients to approximate the global gradient. The introduction of momentums in the proximal gradient descent step, replacing tracking variables, reduces the variance introduced by stochastic gradients. Additionally, DEPOSITUM supports local updates of client variables, significantly reducing communication costs. Theoretical analysis demonstrates that DEPOSITUM achieves an expected $\epsilon$-stationary point with an iteration complexity of $\mathcal{O}(1/\epsilon^2)$. The proximal gradient, consensus errors, and gradient estimation errors decrease at a sublinear rate of $\mathcal{O}(1/T)$. With appropriate parameter selection, the algorithm achieves network-independent linear speedup without requiring mega-batch sampling. Finally, we apply DEPOSITUM to the training of neural networks on real-world datasets, systematically examining the influence of various hyperparameters on its performance. Comparisons with other federated composite optimization algorithms validate the effectiveness of the proposed method.

X Modality Assisting RGBT Object Tracking

Learning robust multi-modal feature representations is critical for boosting tracking performance. To this end, we propose a novel X Modality Assisting Network (X-Net) to shed light on the impact of the fusion paradigm by decoupling the visual object tracking into three distinct levels, facilitating subsequent processing. Firstly, to tackle the feature learning hurdles stemming from significant differences between RGB and thermal modalities, a plug-and-play pixel-level generation module (PGM) is proposed based on self-knowledge distillation learning, which effectively generates X modality to bridge the gap between the dual patterns while reducing noise interference. Subsequently, to further achieve the optimal sample feature representation and facilitate cross-modal interactions, we propose a feature-level interaction module (FIM) that incorporates a mixed feature interaction transformer and a spatial-dimensional feature translation strategy. Ultimately, aiming at random drifting due to missing instance features, we propose a flexible online optimized strategy called the decision-level refinement module (DRM), which contains optical flow and refinement mechanisms. Experiments are conducted on three benchmarks to verify that the proposed X-Net outperforms state-of-the-art trackers.

MG-Skip: Random Multi-Gossip Skipping Method for Nonsmooth Distributed Optimization

Distributed optimization methods with probabilistic local updates have recently gained attention for their provable ability to communication acceleration. Nevertheless, this capability is effective only when the loss function is smooth and the network is sufficiently well-connected. In this paper, we propose the first linear convergent method MG-Skip with probabilistic local updates for nonsmooth distributed optimization. Without any extra condition for the network connectivity, MG-Skip allows for the multiple-round gossip communication to be skipped in most iterations, while its iteration complexity is $\mathcal{O}\left(\kappa \log \frac{1}{\epsilon}\right)$ and communication complexity is only $\mathcal{O}\left(\sqrt{\frac{\kappa}{(1-\rho)}} \log \frac{1}{\epsilon}\right)$, where $\kappa$ is the condition number of the loss function and $\rho$ reflects the connectivity of the network topology. To the best of our knowledge, MG-Skip achieves the best communication complexity when the loss function has the smooth (strongly convex)+nonsmooth (convex) composite form.

RandCom: Random Communication Skipping Method for Decentralized Stochastic Optimization

Distributed optimization methods with random communication skips are gaining increasing attention due to their proven benefits in accelerating communication complexity. Nevertheless, existing research mainly focuses on centralized communication protocols for strongly convex deterministic settings. In this work, we provide a decentralized optimization method called RandCom, which incorporates probabilistic local updates. We analyze the performance of RandCom in stochastic non-convex, convex, and strongly convex settings and demonstrate its ability to asymptotically reduce communication overhead by the probability of communication. Additionally, we prove that RandCom achieves linear speedup as the number of nodes increases. In stochastic strongly convex settings, we further prove that RandCom can achieve linear speedup with network-independent stepsizes. Moreover, we apply RandCom to federated learning and provide positive results concerning the potential for achieving linear speedup and the suitability of the probabilistic local update approach for non-convex settings.

A data-driven rutting depth short-time prediction model with metaheuristic optimization for asphalt pavements based on RIOHTrack

Rutting of asphalt pavements is a crucial design criterion in various pavement design guides. A good road transportation base can provide security for the transportation of oil and gas in road transportation. This study attempts to develop a robust artificial intelligence model to estimate different asphalt pavements' rutting depth clips, temperature, and load axes as primary characteristics. The experiment data were obtained from 19 asphalt pavements with different crude oil sources on a 2.038 km long full-scale field accelerated pavement test track (RIOHTrack, Road Track Institute) in Tongzhou, Beijing. In addition, this paper also proposes to build complex networks with different pavement rutting depths through complex network methods and the Louvain algorithm for community detection. The most critical structural elements can be selected from different asphalt pavement rutting data, and similar structural elements can be found. An extreme learning machine algorithm with residual correction (RELM) is designed and optimized using an independent adaptive particle swarm algorithm. The experimental results of the proposed method are compared with several classical machine learning algorithms, with predictions of Average Root Mean Squared Error, Average Mean Absolute Error, and Average Mean Absolute Percentage Error for 19 asphalt pavements reaching 1.742, 1.363, and 1.94\% respectively. The experiments demonstrate that the RELM algorithm has an advantage over classical machine learning methods in dealing with non-linear problems in road engineering. Notably, the method ensures the adaptation of the simulated environment to different levels of abstraction through the cognitive analysis of the production environment parameters.

Decentralized Inexact Proximal Gradient Method With Network-Independent Stepsizes for Convex Composite Optimization

This paper considers decentralized convex composite optimization over undirected and connected networks, where the local loss function contains both smooth and nonsmooth terms. For this problem, a novel CTA (Combine-Then-Adapt)-based decentralized algorithm is proposed under uncoordinated network-independent constant stepsizes. Particularly, the proposed algorithm only needs to approximately solve a sequence of proximal mappings, which benefits the decentralized composite optimization where the proximal mappings of the nonsmooth loss functions may not have analytic solutions. For the general convex case, we prove the O(1/k) convergence rate of the proposed algorithm, which can be improved to o(1/k) if the proximal mappings are solved exactly. Moreover, with metric subregularity, we establish the linear convergence rate. Finally, the numerical experiments demonstrate the efficiency of the algorithm.

BALPA: A Balanced Primal-Dual Algorithm for Nonsmooth Optimization with Application to Distributed Optimization

In this paper, we propose a novel primal-dual proximal splitting algorithm (PD-PSA), named BALPA, for the composite optimization problem with equality constraints, where the loss function consists of a smooth term and a nonsmooth term composed with a linear mapping. In BALPA, the dual update is designed as a proximal point for a time-varying quadratic function, which balances the implementation of primal and dual update and retains the proximity-induced feature of classic PD-PSAs. In addition, by this balance, BALPA eliminates the inefficiency of classic PD-PSAs for composite optimization problems in which the Euclidean norm of the linear mapping or the equality constraint mapping is large. Therefore, BALPA not only inherits the advantages of simple structure and easy implementation of classic PD-PSAs but also ensures a fast convergence when these norms are large. Moreover, we propose a stochastic version of BALPA (S-BALPA) and apply the developed BALPA to distributed optimization to devise a new distributed optimization algorithm. Furthermore, a comprehensive convergence analysis for BALPA and S-BALPA is conducted, respectively. Finally, numerical experiments demonstrate the efficiency of the proposed algorithms.

LP-BFGS attack: An adversarial attack based on the Hessian with limited pixels

Deep neural networks are vulnerable to adversarial attacks. Most white-box attacks are based on the gradient of models to the input. Since the computation and memory budget, adversarial attacks based on the Hessian information are not paid enough attention. In this work, we study the attack performance and computation cost of the attack method based on the Hessian with a limited perturbation pixel number. Specifically, we propose the Limited Pixel BFGS (LP-BFGS) attack method by incorporating the BFGS algorithm. Some pixels are selected as perturbation pixels by the Integrated Gradient algorithm, which are regarded as optimization variables of the LP-BFGS attack. Experimental results across different networks and datasets with various perturbation pixel numbers demonstrate our approach has a comparable attack with an acceptable computation compared with existing solutions.

DISA: A Dual Inexact Splitting Algorithm for Distributed Convex Composite Optimization

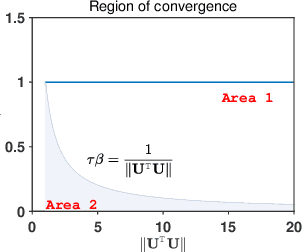
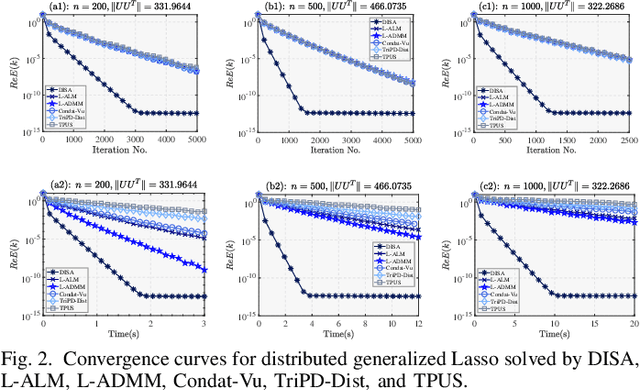
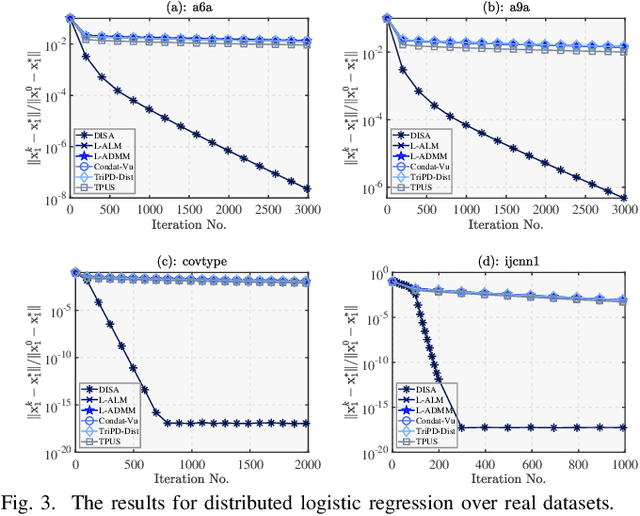
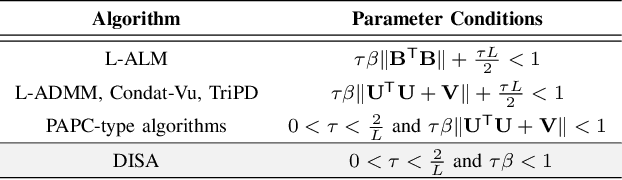
This paper proposes a novel dual inexact splitting algorithm (DISA) for the distributed convex composite optimization problem, where the local loss function consists of an $L$-smooth term and a possibly nonsmooth term which is composed with a linear operator. We prove that DISA is convergent when the primal and dual stepsizes $\tau$, $\beta$ satisfy $0<\tau<{2}/{L}$ and $0<\tau\beta <1$. Compared with existing primal-dual proximal splitting algorithms (PD-PSAs), DISA overcomes the dependence of the convergence stepsize range on the Euclidean norm of the linear operator. It implies that DISA allows for larger stepsizes when the Euclidean norm is large, thus ensuring fast convergence of it. Moreover, we establish the sublinear and linear convergence rate of DISA under general convexity and metric subregularity, respectively. Furthermore, an approximate iterative version of DISA is provided, and the global convergence and sublinear convergence rate of this approximate version are proved. Finally, numerical experiments not only corroborate the theoretical analyses but also indicate that DISA achieves a significant acceleration compared with the existing PD-PSAs.