Accelerated Stochastic Min-Max Optimization Based on Bias-corrected Momentum

Lower-bound analyses for nonconvex strongly-concave minimax optimization problems have shown that stochastic first-order algorithms require at least $\mathcal{O}(\varepsilon^{-4})$ oracle complexity to find an $\varepsilon$-stationary point. Some works indicate that this complexity can be improved to $\mathcal{O}(\varepsilon^{-3})$ when the loss gradient is Lipschitz continuous. The question of achieving enhanced convergence rates under distinct conditions, remains unresolved. In this work, we address this question for optimization problems that are nonconvex in the minimization variable and strongly concave or Polyak-Lojasiewicz (PL) in the maximization variable. We introduce novel bias-corrected momentum algorithms utilizing efficient Hessian-vector products. We establish convergence conditions and demonstrate a lower iteration complexity of $\mathcal{O}(\varepsilon^{-3})$ for the proposed algorithms. The effectiveness of the method is validated through applications to robust logistic regression using real-world datasets.

Diffusion Stochastic Optimization for Min-Max Problems

The optimistic gradient method is useful in addressing minimax optimization problems. Motivated by the observation that the conventional stochastic version suffers from the need for a large batch size on the order of $\mathcal{O}(\varepsilon^{-2})$ to achieve an $\varepsilon$-stationary solution, we introduce and analyze a new formulation termed Diffusion Stochastic Same-Sample Optimistic Gradient (DSS-OG). We prove its convergence and resolve the large batch issue by establishing a tighter upper bound, under the more general setting of nonconvex Polyak-Lojasiewicz (PL) risk functions. We also extend the applicability of the proposed method to the distributed scenario, where agents communicate with their neighbors via a left-stochastic protocol. To implement DSS-OG, we can query the stochastic gradient oracles in parallel with some extra memory overhead, resulting in a complexity comparable to its conventional counterpart. To demonstrate the efficacy of the proposed algorithm, we conduct tests by training generative adversarial networks.

RandCom: Random Communication Skipping Method for Decentralized Stochastic Optimization

Distributed optimization methods with random communication skips are gaining increasing attention due to their proven benefits in accelerating communication complexity. Nevertheless, existing research mainly focuses on centralized communication protocols for strongly convex deterministic settings. In this work, we provide a decentralized optimization method called RandCom, which incorporates probabilistic local updates. We analyze the performance of RandCom in stochastic non-convex, convex, and strongly convex settings and demonstrate its ability to asymptotically reduce communication overhead by the probability of communication. Additionally, we prove that RandCom achieves linear speedup as the number of nodes increases. In stochastic strongly convex settings, we further prove that RandCom can achieve linear speedup with network-independent stepsizes. Moreover, we apply RandCom to federated learning and provide positive results concerning the potential for achieving linear speedup and the suitability of the probabilistic local update approach for non-convex settings.

On the Performance of Gradient Tracking with Local Updates

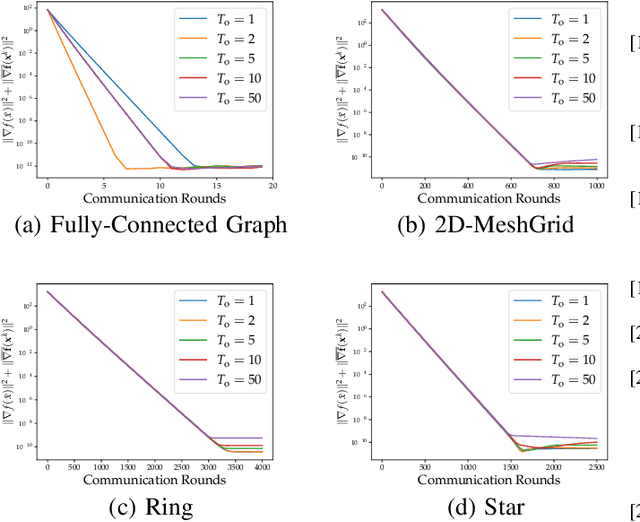
We study the decentralized optimization problem where a network of $n$ agents seeks to minimize the average of a set of heterogeneous non-convex cost functions distributedly. State-of-the-art decentralized algorithms like Exact Diffusion~(ED) and Gradient Tracking~(GT) involve communicating every iteration. However, communication is expensive, resource intensive, and slow. In this work, we analyze a locally updated GT method (LU-GT), where agents perform local recursions before interacting with their neighbors. While local updates have been shown to reduce communication overhead in practice, their theoretical influence has not been fully characterized. We show LU-GT has the same communication complexity as the Federated Learning setting but allows arbitrary network topologies. In addition, we prove that the number of local updates does not degrade the quality of the solution achieved by LU-GT. Numerical examples reveal that local updates can lower communication costs in certain regimes (e.g., well-connected graphs).

Removing Data Heterogeneity Influence Enhances Network Topology Dependence of Decentralized SGD

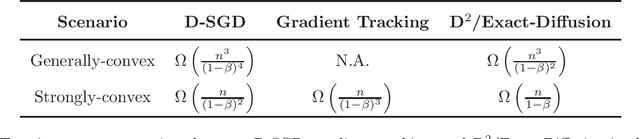
We consider decentralized stochastic optimization problems where a network of agents each owns a local cost function cooperate to find a minimizer of the global-averaged cost. A widely studied decentralized algorithm for this problem is D-SGD in which each node applies a stochastic gradient descent step, then averages its estimate with its neighbors. D-SGD is attractive due to its efficient single-iteration communication and can achieve linear speedup in convergence (in terms of the network size). However, D-SGD is very sensitive to the network topology. For smooth objective functions, the transient stage (which measures how fast the algorithm can reach the linear speedup stage) of D-SGD is on the order of $O(n/(1-\beta)^2)$ and $O(n^3/(1-\beta)^4)$ for strongly convex and generally convex cost functions, respectively, where $1-\beta \in (0,1)$ is a topology-dependent quantity that approaches $0$ for a large and sparse network. Hence, D-SGD suffers from slow convergence for large and sparse networks. In this work, we study the non-asymptotic convergence property of the D$^2$/Exact-diffusion algorithm. By eliminating the influence of data heterogeneity between nodes, D$^2$/Exact-diffusion is shown to have an enhanced transient stage that are on the order of $O(n/(1-\beta))$ and $O(n^3/(1-\beta)^2)$ for strongly convex and generally convex cost functions, respectively. Moreover, we provide a lower bound of the transient stage of D-SGD under homogeneous data distributions, which coincides with the transient stage of D$^2$/Exact-diffusion in the strongly-convex setting. These results show that removing the influence of data heterogeneity can ameliorate the network topology dependence of D-SGD. Compared with existing decentralized algorithms bounds, D$^2$/Exact-diffusion is least sensitive to network topology.

A Multi-Agent Primal-Dual Strategy for Composite Optimization over Distributed Features

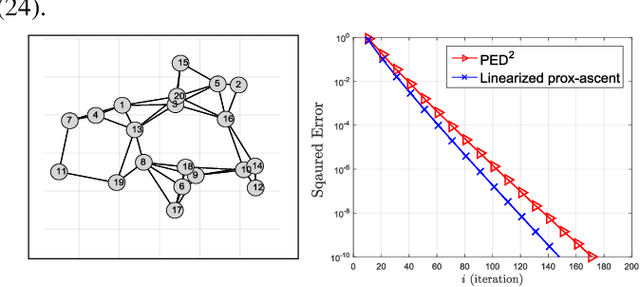
This work studies multi-agent sharing optimization problems with the objective function being the sum of smooth local functions plus a convex (possibly non-smooth) function coupling all agents. This scenario arises in many machine learning and engineering applications, such as regression over distributed features and resource allocation. We reformulate this problem into an equivalent saddle-point problem, which is amenable to decentralized solutions. We then propose a proximal primal-dual algorithm and establish its linear convergence to the optimal solution when the local functions are strongly-convex. To our knowledge, this is the first linearly convergent decentralized algorithm for multi-agent sharing problems with a general convex (possibly non-smooth) coupling function.

On the Performance of Exact Diffusion over Adaptive Networks

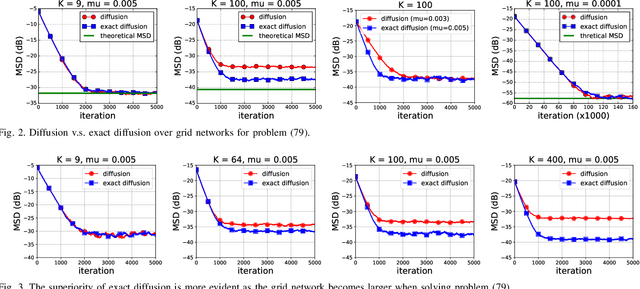
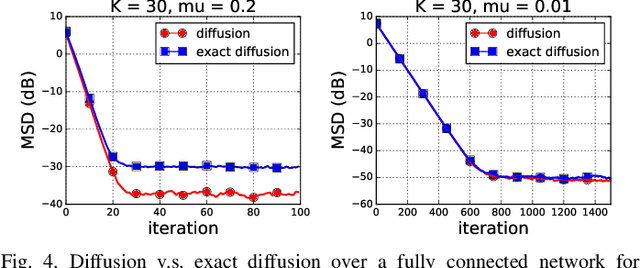
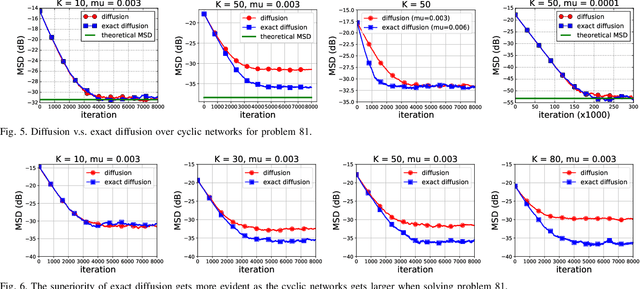
Various bias-correction methods such as EXTRA, DIGing, and exact diffusion have been proposed recently to solve distributed deterministic optimization problems. These methods employ constant step-sizes and converge linearly to the {\em exact} solution under proper conditions. However, their performance under stochastic and adaptive settings remains unclear. It is still unknown whether the bias-correction is necessary over adaptive networks. By studying exact diffusion and examining its steady-state performance under stochastic scenarios, this paper provides affirmative results. It is shown that the correction step in exact diffusion leads to better steady-state performance than traditional methods. It is also analytically shown the superiority of exact diffusion is more evident over badly-connected network topologies.