Cross-platform Prediction of Depression Treatment Outcome Using Location Sensory Data on Smartphones

Currently, depression treatment relies on closely monitoring patients response to treatment and adjusting the treatment as needed. Using self-reported or physician-administrated questionnaires to monitor treatment response is, however, burdensome, costly and suffers from recall bias. In this paper, we explore using location sensory data collected passively on smartphones to predict treatment outcome. To address heterogeneous data collection on Android and iOS phones, the two predominant smartphone platforms, we explore using domain adaptation techniques to map their data to a common feature space, and then use the data jointly to train machine learning models. Our results show that this domain adaptation approach can lead to significantly better prediction than that with no domain adaptation. In addition, our results show that using location features and baseline self-reported questionnaire score can lead to F1 score up to 0.67, comparable to that obtained using periodic self-reported questionnaires, indicating that using location data is a promising direction for predicting depression treatment outcome.

Certifying Adapters: Enabling and Enhancing the Certification of Classifier Adversarial Robustness

Randomized smoothing has become a leading method for achieving certified robustness in deep classifiers against l_{p}-norm adversarial perturbations. Current approaches for achieving certified robustness, such as data augmentation with Gaussian noise and adversarial training, require expensive training procedures that tune large models for different Gaussian noise levels and thus cannot leverage high-performance pre-trained neural networks. In this work, we introduce a novel certifying adapters framework (CAF) that enables and enhances the certification of classifier adversarial robustness. Our approach makes few assumptions about the underlying training algorithm or feature extractor and is thus broadly applicable to different feature extractor architectures (e.g., convolutional neural networks or vision transformers) and smoothing algorithms. We show that CAF (a) enables certification in uncertified models pre-trained on clean datasets and (b) substantially improves the performance of certified classifiers via randomized smoothing and SmoothAdv at multiple radii in CIFAR-10 and ImageNet. We demonstrate that CAF achieves improved certified accuracies when compared to methods based on random or denoised smoothing, and that CAF is insensitive to certifying adapter hyperparameters. Finally, we show that an ensemble of adapters enables a single pre-trained feature extractor to defend against a range of noise perturbation scales.

Weakly Supervised Change Detection via Knowledge Distillation and Multiscale Sigmoid Inference

Change detection, which aims to detect spatial changes from a pair of multi-temporal images due to natural or man-made causes, has been widely applied in remote sensing, disaster management, urban management, etc. Most existing change detection approaches, however, are fully supervised and require labor-intensive pixel-level labels. To address this, we develop a novel weakly supervised change detection technique via Knowledge Distillation and Multiscale Sigmoid Inference (KD-MSI) that leverages image-level labels. In our approach, the Class Activation Maps (CAM) are utilized not only to derive a change probability map but also to serve as a foundation for the knowledge distillation process. This is done through a joint training strategy of the teacher and student networks, enabling the student network to highlight potential change areas more accurately than teacher network based on image-level labels. Moreover, we designed a Multiscale Sigmoid Inference (MSI) module as a post processing step to further refine the change probability map from the trained student network. Empirical results on three public datasets, i.e., WHU-CD, DSIFN-CD, and LEVIR-CD, demonstrate that our proposed technique, with its integrated training strategy, significantly outperforms the state-of-the-art.

Distilling Adversarial Robustness Using Heterogeneous Teachers

Achieving resiliency against adversarial attacks is necessary prior to deploying neural network classifiers in domains where misclassification incurs substantial costs, e.g., self-driving cars or medical imaging. Recent work has demonstrated that robustness can be transferred from an adversarially trained teacher to a student model using knowledge distillation. However, current methods perform distillation using a single adversarial and vanilla teacher and consider homogeneous architectures (i.e., residual networks) that are susceptible to misclassify examples from similar adversarial subspaces. In this work, we develop a defense framework against adversarial attacks by distilling adversarial robustness using heterogeneous teachers (DARHT). In DARHT, the student model explicitly represents teacher logits in a student-teacher feature map and leverages multiple teachers that exhibit low adversarial example transferability (i.e., exhibit high performance on dissimilar adversarial examples). Experiments on classification tasks in both white-box and black-box scenarios demonstrate that DARHT achieves state-of-the-art clean and robust accuracies when compared to competing adversarial training and distillation methods in the CIFAR-10, CIFAR-100, and Tiny ImageNet datasets. Comparisons with homogeneous and heterogeneous teacher sets suggest that leveraging teachers with low adversarial example transferability increases student model robustness.

Heterogeneous Graph Sparsification for Efficient Representation Learning

Graph sparsification is a powerful tool to approximate an arbitrary graph and has been used in machine learning over homogeneous graphs. In heterogeneous graphs such as knowledge graphs, however, sparsification has not been systematically exploited to improve efficiency of learning tasks. In this work, we initiate the study on heterogeneous graph sparsification and develop sampling-based algorithms for constructing sparsifiers that are provably sparse and preserve important information in the original graphs. We have performed extensive experiments to confirm that the proposed method can improve time and space complexities of representation learning while achieving comparable, or even better performance in subsequent graph learning tasks based on the learned embedding.

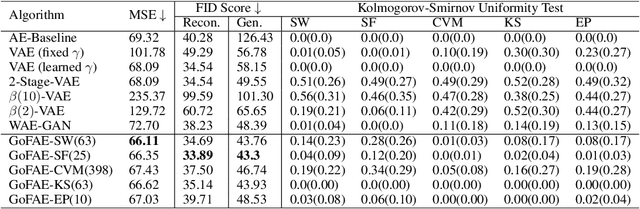
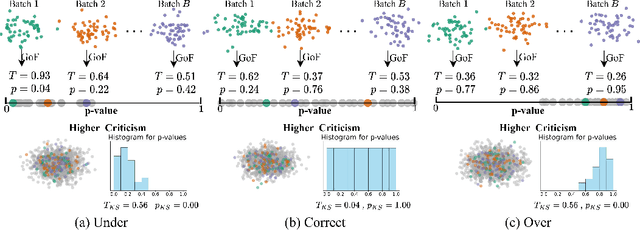
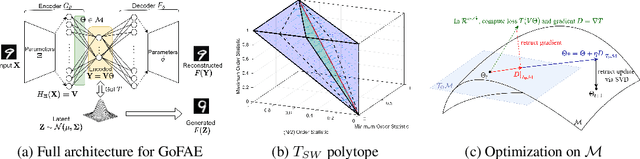
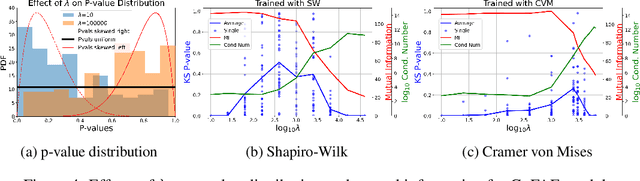
Auto-Encoding Goodness of Fit

For generative autoencoders to learn a meaningful latent representation for data generation, a careful balance must be achieved between reconstruction error and how close the distribution in the latent space is to the prior. However, this balance is challenging to achieve due to a lack of criteria that work both at the mini-batch (local) and aggregated posterior (global) level. Goodness of fit (GoF) hypothesis tests provide a measure of statistical indistinguishability between the latent distribution and a target distribution class. In this work, we develop the Goodness of Fit Autoencoder (GoFAE), which incorporates hypothesis tests at two levels. At the mini-batch level, it uses GoF test statistics as regularization objectives. At a more global level, it selects a regularization coefficient based on higher criticism, i.e., a test on the uniformity of the local GoF p-values. We justify the use of GoF tests by providing a relaxed $L_2$-Wasserstein bound on the distance between the latent distribution and target prior. We propose to use GoF tests and prove that optimization based on these tests can be done with stochastic gradient (SGD) descent on a compact Riemannian manifold. Empirically, we show that our higher criticism parameter selection procedure balances reconstruction and generation using mutual information and uniformity of p-values respectively. Finally, we show that GoFAE achieves comparable FID scores and mean squared errors with competing deep generative models while retaining statistical indistinguishability from Gaussian in the latent space based on a variety of hypothesis tests.

A Length Adaptive Algorithm-Hardware Co-design of Transformer on FPGA Through Sparse Attention and Dynamic Pipelining

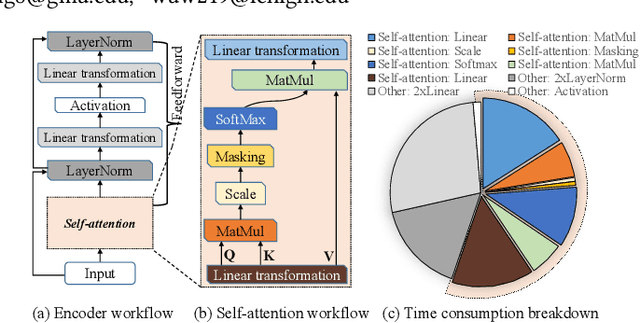
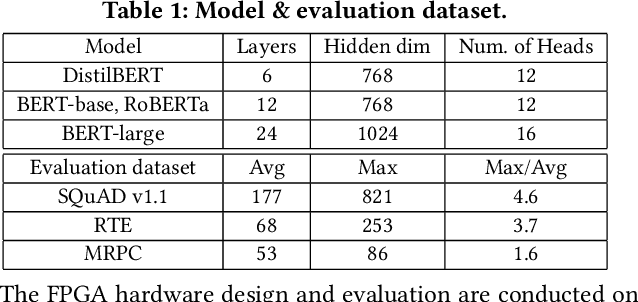
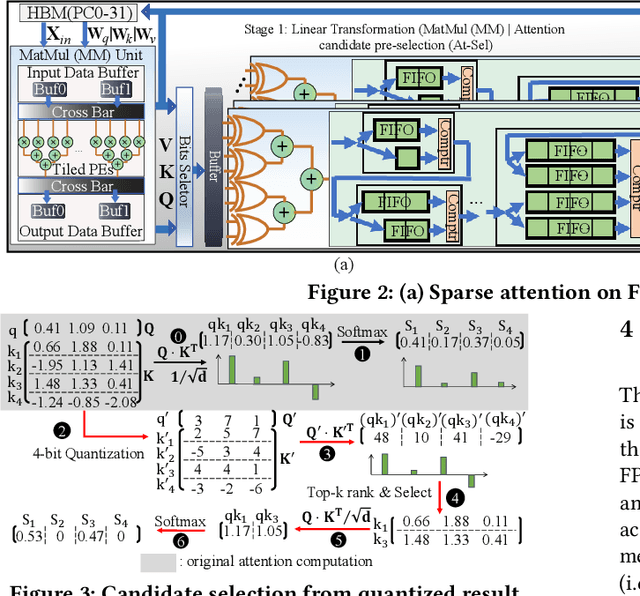
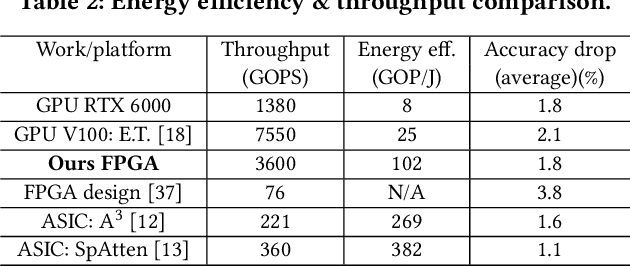
Transformers are considered one of the most important deep learning models since 2018, in part because it establishes state-of-the-art (SOTA) records and could potentially replace existing Deep Neural Networks (DNNs). Despite the remarkable triumphs, the prolonged turnaround time of Transformer models is a widely recognized roadblock. The variety of sequence lengths imposes additional computing overhead where inputs need to be zero-padded to the maximum sentence length in the batch to accommodate the parallel computing platforms. This paper targets the field-programmable gate array (FPGA) and proposes a coherent sequence length adaptive algorithm-hardware co-design for Transformer acceleration. Particularly, we develop a hardware-friendly sparse attention operator and a length-aware hardware resource scheduling algorithm. The proposed sparse attention operator brings the complexity of attention-based models down to linear complexity and alleviates the off-chip memory traffic. The proposed length-aware resource hardware scheduling algorithm dynamically allocates the hardware resources to fill up the pipeline slots and eliminates bubbles for NLP tasks. Experiments show that our design has very small accuracy loss and has 80.2 $\times$ and 2.6 $\times$ speedup compared to CPU and GPU implementation, and 4 $\times$ higher energy efficiency than state-of-the-art GPU accelerator optimized via CUBLAS GEMM.

An Efficient Algorithm for Deep Stochastic Contextual Bandits

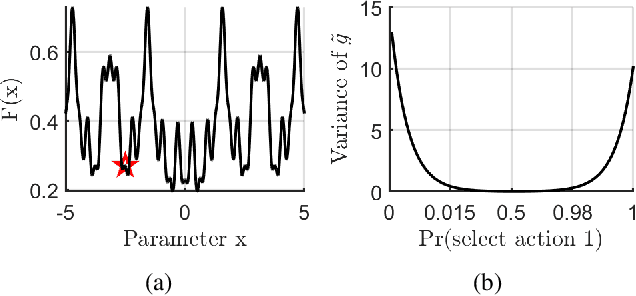
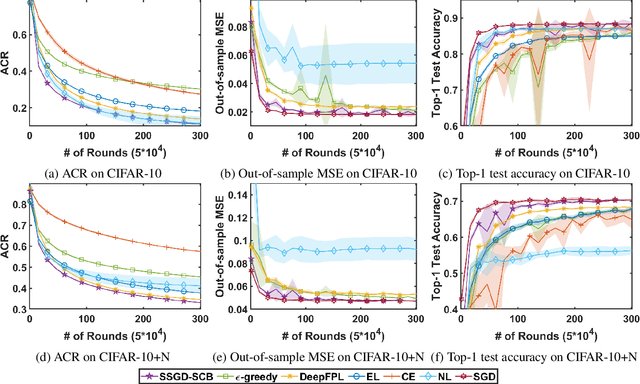
In stochastic contextual bandit (SCB) problems, an agent selects an action based on certain observed context to maximize the cumulative reward over iterations. Recently there have been a few studies using a deep neural network (DNN) to predict the expected reward for an action, and the DNN is trained by a stochastic gradient based method. However, convergence analysis has been greatly ignored to examine whether and where these methods converge. In this work, we formulate the SCB that uses a DNN reward function as a non-convex stochastic optimization problem, and design a stage-wise stochastic gradient descent algorithm to optimize the problem and determine the action policy. We prove that with high probability, the action sequence chosen by this algorithm converges to a greedy action policy respecting a local optimal reward function. Extensive experiments have been performed to demonstrate the effectiveness and efficiency of the proposed algorithm on multiple real-world datasets.

Escaping Saddle Points with Stochastically Controlled Stochastic Gradient Methods

Stochastically controlled stochastic gradient (SCSG) methods have been proved to converge efficiently to first-order stationary points which, however, can be saddle points in nonconvex optimization. It has been observed that a stochastic gradient descent (SGD) step introduces anistropic noise around saddle points for deep learning and non-convex half space learning problems, which indicates that SGD satisfies the correlated negative curvature (CNC) condition for these problems. Therefore, we propose to use a separate SGD step to help the SCSG method escape from strict saddle points, resulting in the CNC-SCSG method. The SGD step plays a role similar to noise injection but is more stable. We prove that the resultant algorithm converges to a second-order stationary point with a convergence rate of $\tilde{O}( \epsilon^{-2} log( 1/\epsilon))$ where $\epsilon$ is the pre-specified error tolerance. This convergence rate is independent of the problem dimension, and is faster than that of CNC-SGD. A more general framework is further designed to incorporate the proposed CNC-SCSG into any first-order method for the method to escape saddle points. Simulation studies illustrate that the proposed algorithm can escape saddle points in much fewer epochs than the gradient descent methods perturbed by either noise injection or a SGD step.

Discrete Graph Structure Learning for Forecasting Multiple Time Series

Time series forecasting is an extensively studied subject in statistics, economics, and computer science. Exploration of the correlation and causation among the variables in a multivariate time series shows promise in enhancing the performance of a time series model. When using deep neural networks as forecasting models, we hypothesize that exploiting the pairwise information among multiple (multivariate) time series also improves their forecast. If an explicit graph structure is known, graph neural networks (GNNs) have been demonstrated as powerful tools to exploit the structure. In this work, we propose learning the structure simultaneously with the GNN if the graph is unknown. We cast the problem as learning a probabilistic graph model through optimizing the mean performance over the graph distribution. The distribution is parameterized by a neural network so that discrete graphs can be sampled differentiably through reparameterization. Empirical evaluations show that our method is simpler, more efficient, and better performing than a recently proposed bilevel learning approach for graph structure learning, as well as a broad array of forecasting models, either deep or non-deep learning based, and graph or non-graph based.