Jan-Willem van de Meent
Deep Markov Spatio-Temporal Factorization
Mar 22, 2020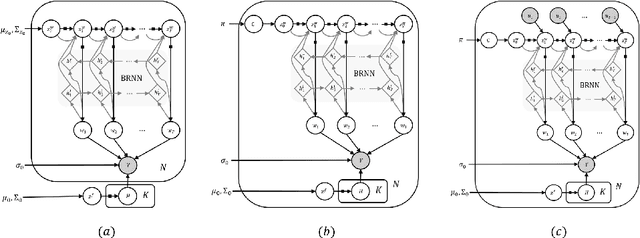

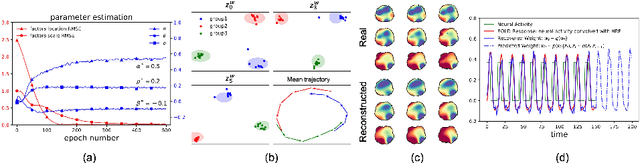

Abstract:We introduce deep Markov spatio-temporal factorization (DMSTF), a deep generative model for spatio-temporal data. Like other factor analysis methods, DMSTF approximates high-dimensional data by a product between time-dependent weights and spatially dependent factors. These weights and factors are in turn represented in terms of lower-dimensional latent variables that we infer using stochastic variational inference. The innovation in DMSTF is that we parameterize weights in terms of a deep Markovian prior, which is able to characterize nonlinear temporal dynamics. We parameterize the corresponding variational distribution using a bidirectional recurrent network. This results in a flexible family of hierarchical deep generative factor analysis models that can be extended to perform time series clustering, or perform factor analysis in the presence of a control signal. Our experiments, which consider simulated data, fMRI data, and traffic data, demonstrate that DMSTF outperforms related methods in terms of reconstruction accuracy and can perform forecasting in a variety domains with nonlinear temporal transitions.
Learning discrete state abstractions with deep variational inference
Mar 09, 2020
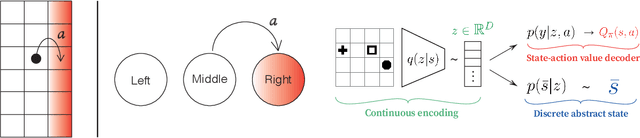
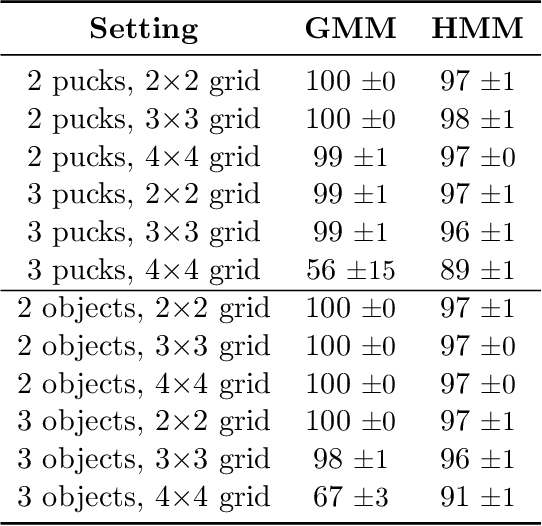
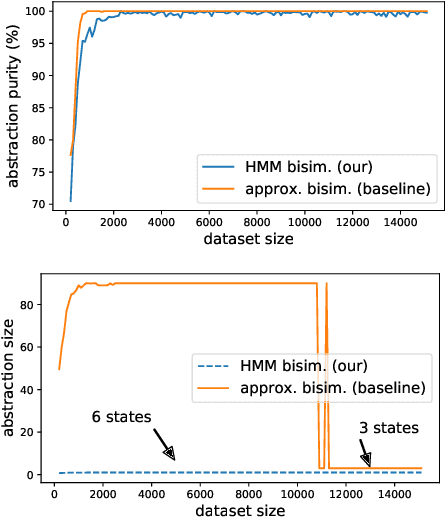
Abstract:Abstraction is crucial for effective sequential decision making in domains with large state spaces. In this work, we propose a variational information bottleneck method for learning approximate bisimulations, a type of state abstraction. We use a deep neural net encoder to map states onto continuous embeddings. The continuous latent space is then compressed into a discrete representation using an action-conditioned hidden Markov model, which is trained end-to-end with the neural network. Our method is suited for environments with high-dimensional states and learns from a stream of experience collected by an agent acting in a Markov decision process. Through a learned discrete abstract model, we can efficiently plan for unseen goals in a multi-goal Reinforcement Learning setting. We test our method in simplified robotic manipulation domains with image states. We also compare it against previous model-based approaches to finding bisimulations in discrete grid-world-like environments.
Evaluating Combinatorial Generalization in Variational Autoencoders
Nov 11, 2019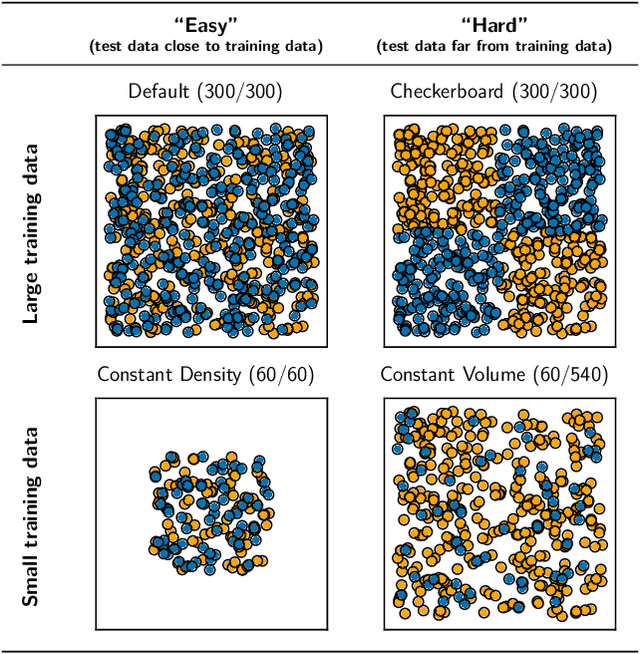
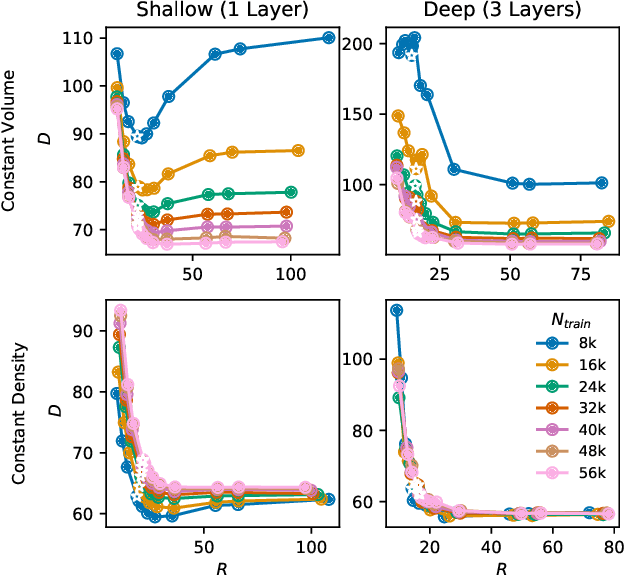
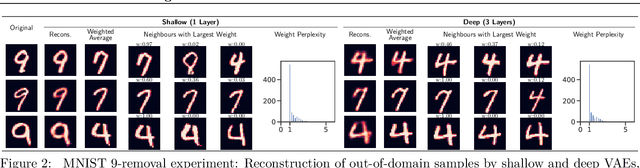

Abstract:We evaluate the ability of variational autoencoders to generalize to unseen examples in domains with a large combinatorial space of feature values. Our experiments systematically evaluate the effect of network width, depth, regularization, and the typical distance between the training and test examples. Increasing network capacity benefits generalization in easy problems, where test-set examples are similar to training examples. In more difficult problems, increasing capacity deteriorates generalization when optimizing the standard VAE objective, but once again improves generalization when we decrease the KL regularization. Our results establish that interplay between model capacity and KL regularization is not clear cut; we need to take the typical distance between train and test examples into account when evaluating generalization.
Amortized Population Gibbs Samplers with Neural Sufficient Statistics
Nov 04, 2019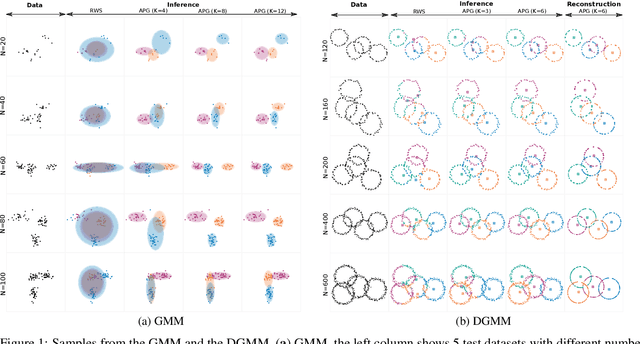
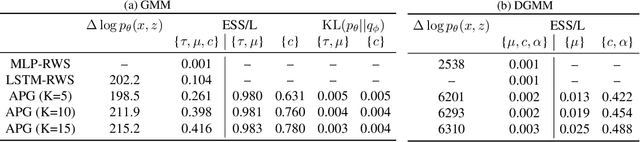
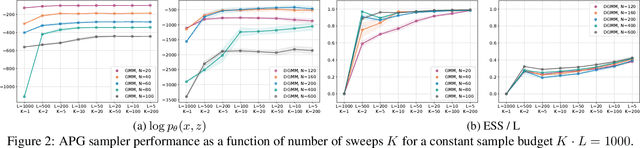

Abstract:We develop amortized population Gibbs (APG) samplers, a new class of autoencoding variational methods for deep probabilistic models. APG samplers construct high-dimensional proposals by iterating over updates to lower-dimensional blocks of variables. Each conditional update is a neural proposal, which we train by minimizing the inclusive KL divergence relative to the conditional posterior. To appropriately account for the size of the input data, we develop a new parameterization in terms of neural sufficient statistics, resulting in quasi-conjugate variational approximations. Experiments demonstrate that learned proposals converge to the known analytical conditional posterior in conjugate models, and that APG samplers can learn inference networks for highly-structured deep generative models when the conditional posteriors are intractable. Here APG samplers offer a path toward scaling up stochastic variational methods to models in which standard autoencoding architectures fail to produce accurate samples.
Neural Topographic Factor Analysis for fMRI Data
Jun 21, 2019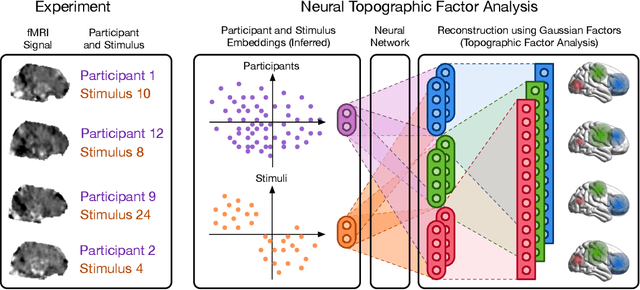

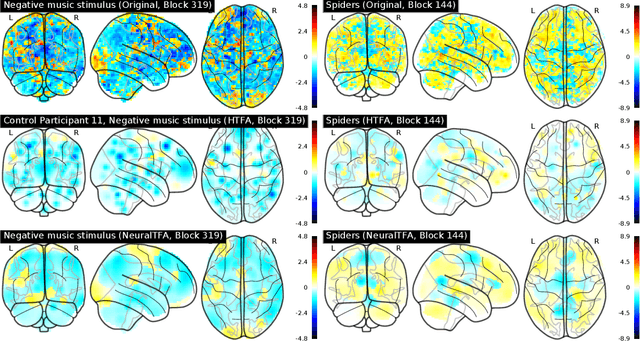
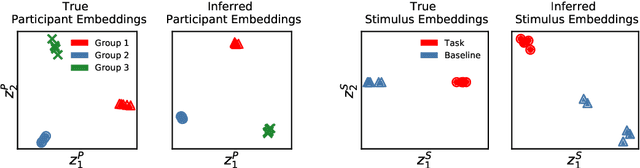
Abstract:Neuroimaging experiments produce a large volume (gigabytes) of high-dimensional spatio-temporal data for a small number of sampled participants and stimuli. Analyses of this data commonly compute averages over all trials, ignoring variation within groups of participants and stimuli. To enable the analysis of fMRI data without this implicit assumption of uniformity, we propose Neural Topographic Factor Analysis (NTFA), a deep generative model that parameterizes factors as functions of embeddings for participants and stimuli. We evaluate NTFA on a synthetically generated dataset as well as on three datasets from fMRI experiments. Our results demonstrate that NTFA yields more accurate reconstructions than a state-of-the-art method with fewer parameters. Moreover, learned embeddings uncover latent categories of participants and stimuli, which suggests that NTFA takes a first step towards reasoning about individual variation in fMRI experiments.
Structured Neural Topic Models for Reviews
Jan 02, 2019
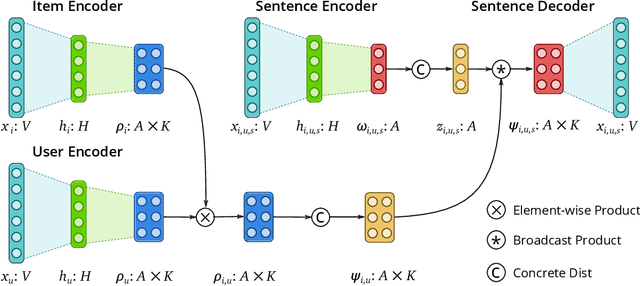

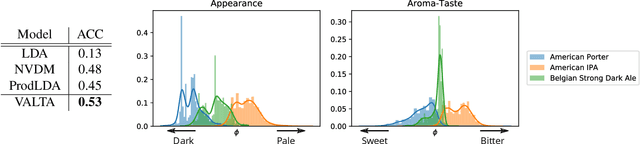
Abstract:We present Variational Aspect-based Latent Topic Allocation (VALTA), a family of autoencoding topic models that learn aspect-based representations of reviews. VALTA defines a user-item encoder that maps bag-of-words vectors for combined reviews associated with each paired user and item onto structured embeddings, which in turn define per-aspect topic weights. We model individual reviews in a structured manner by inferring an aspect assignment for each sentence in a given review, where the per-aspect topic weights obtained by the user-item encoder serve to define a mixture over topics, conditioned on the aspect. The result is an autoencoding neural topic model for reviews, which can be trained in a fully unsupervised manner to learn topics that are structured into aspects. Experimental evaluation on large number of datasets demonstrates that aspects are interpretable, yield higher coherence scores than non-structured autoencoding topic model variants, and can be utilized to perform aspect-based comparison and genre discovery.
Can VAEs Generate Novel Examples?
Dec 22, 2018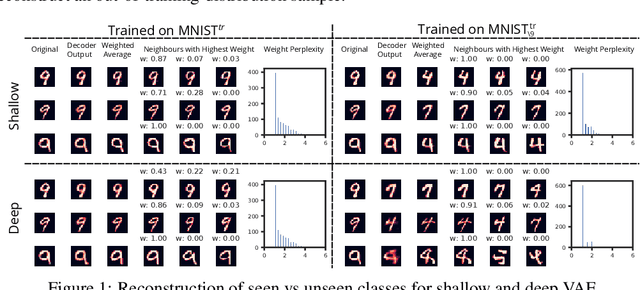
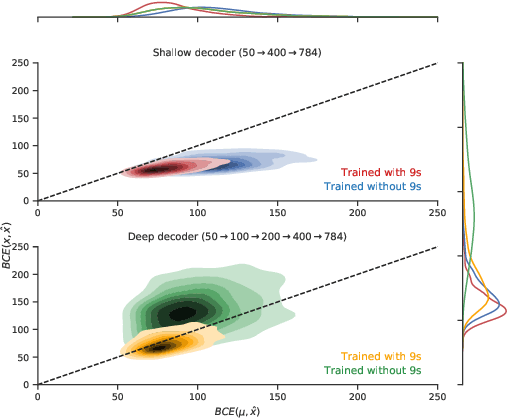

Abstract:An implicit goal in works on deep generative models is that such models should be able to generate novel examples that were not previously seen in the training data. In this paper, we investigate to what extent this property holds for widely employed variational autoencoder (VAE) architectures. VAEs maximize a lower bound on the log marginal likelihood, which implies that they will in principle overfit the training data when provided with a sufficiently expressive decoder. In the limit of an infinite capacity decoder, the optimal generative model is a uniform mixture over the training data. More generally, an optimal decoder should output a weighted average over the examples in the training data, where the magnitude of the weights is determined by the proximity in the latent space. This leads to the hypothesis that, for a sufficiently high capacity encoder and decoder, the VAE decoder will perform nearest-neighbor matching according to the coordinates in the latent space. To test this hypothesis, we investigate generalization on the MNIST dataset. We consider both generalization to new examples of previously seen classes, and generalization to the classes that were withheld from the training set. In both cases, we find that reconstructions are closely approximated by nearest neighbors for higher-dimensional parameterizations. When generalizing to unseen classes however, lower-dimensional parameterizations offer a clear advantage.
Modeling Theory of Mind for Autonomous Agents with Probabilistic Programs
Dec 04, 2018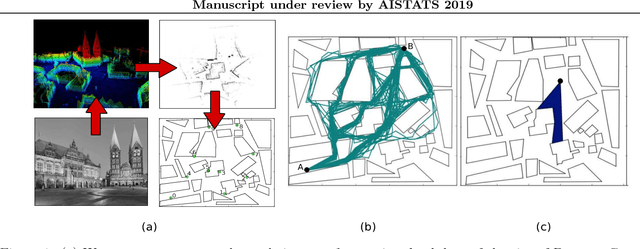

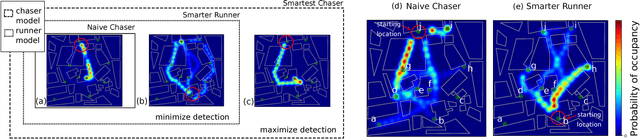
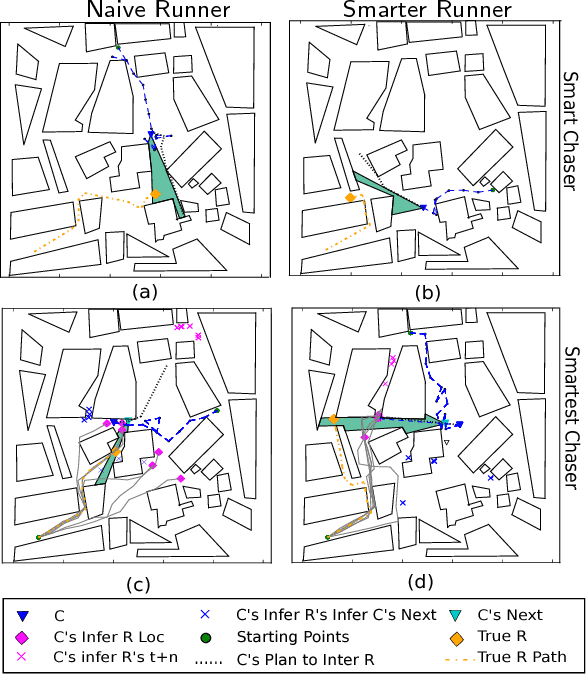
Abstract:As autonomous agents become more ubiquitous, they will eventually have to reason about the mental state of other agents, including those agents' beliefs, desires and goals - so-called theory of mind reasoning. We introduce a collection of increasingly complex theory of mind models of a "chaser" pursuing a "runner", known as the Chaser-Runner model. We show that our implementation is a relatively straightforward theory of mind model that can capture a variety of rich behaviors, which in turn, increase runner detection rates relative to basic (non-theory-of-mind) models. In addition, our paper demonstrates that (1) using a planning-as-inference formulation based on nested importance sampling results in agents simultaneously reasoning about other agents' plans and crafting counter-plans, (2) probabilistic programming is a natural way to describe models in which each uses complex primitives such as path planners to make decisions, and (3) allocating additional computation to perform nested reasoning about agents result in lower-variance estimates of expected utility.
Composing Modeling and Inference Operations with Probabilistic Program Combinators
Nov 29, 2018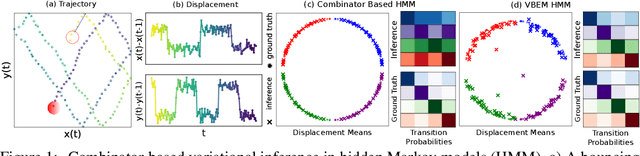

Abstract:Probabilistic programs with dynamic computation graphs can define measures over sample spaces with unbounded dimensionality, which constitute programmatic analogues to Bayesian nonparametrics. Owing to the generality of this model class, inference relies on `black-box' Monte Carlo methods that are often not able to take advantage of conditional independence and exchangeability, which have historically been the cornerstones of efficient inference. We here seek to develop a `middle ground' between probabilistic models with fully dynamic and fully static computation graphs. To this end, we introduce a combinator library for the Probabilistic Torch framework. Combinators are functions that accept models and return transformed models. We assume that models are dynamic, but that model composition is static, in the sense that combinator application takes place prior to evaluating the model on data. Combinators provide primitives for both model and inference composition. Model combinators take the form of classic functional programming constructs such as map and reduce. These constructs define a computation graph at a coarsened level of representation, in which nodes correspond to models, rather than individual variables. Inference combinators implement operations such as importance resampling and application of a transition kernel, which alter the evaluation strategy for a model whilst preserving proper weighting. Owing to this property, models defined using combinators can be trained using stochastic methods that optimize either variational or wake-sleep style objectives. As a validation of this principle, we use combinators to implement black box inference for hidden Markov models.
On Exploration, Exploitation and Learning in Adaptive Importance Sampling
Oct 31, 2018



Abstract:We study adaptive importance sampling (AIS) as an online learning problem and argue for the importance of the trade-off between exploration and exploitation in this adaptation. Borrowing ideas from the bandits literature, we propose Daisee, a partition-based AIS algorithm. We further introduce a notion of regret for AIS and show that Daisee has $\mathcal{O}(\sqrt{T}(\log T)^{\frac{3}{4}})$ cumulative pseudo-regret, where $T$ is the number of iterations. We then extend Daisee to adaptively learn a hierarchical partitioning of the sample space for more efficient sampling and confirm the performance of both algorithms empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge