Density Ratio-Free Doubly Robust Proxy Causal Learning

We study the problem of causal function estimation in the Proxy Causal Learning (PCL) framework, where confounders are not observed but proxies for the confounders are available. Two main approaches have been proposed: outcome bridge-based and treatment bridge-based methods. In this work, we propose two kernel-based doubly robust estimators that combine the strengths of both approaches, and naturally handle continuous and high-dimensional variables. Our identification strategy builds on a recent density ratio-free method for treatment bridge-based PCL; furthermore, in contrast to previous approaches, it does not require indicator functions or kernel smoothing over the treatment variable. These properties make it especially well-suited for continuous or high-dimensional treatments. By using kernel mean embeddings, we have closed-form solutions and strong consistency guarantees. Our estimators outperform existing methods on PCL benchmarks, including a prior doubly robust method that requires both kernel smoothing and density ratio estimation.

Causal mediation analysis with one or multiple mediators: a comparative study

Mediation analysis breaks down the causal effect of a treatment on an outcome into an indirect effect, acting through a third group of variables called mediators, and a direct effect, operating through other mechanisms. Mediation analysis is hard because confounders between treatment, mediators, and outcome blur effect estimates in observational studies. Many estimators have been proposed to adjust on those confounders and provide accurate causal estimates. We consider parametric and non-parametric implementations of classical estimators and provide a thorough evaluation for the estimation of the direct and indirect effects in the context of causal mediation analysis for binary, continuous, and multi-dimensional mediators. We assess several approaches in a comprehensive benchmark on simulated data. Our results show that advanced statistical approaches such as the multiply robust and the double machine learning estimators achieve good performances in most of the simulated settings and on real data. As an example of application, we propose a thorough analysis of factors known to influence cognitive functions to assess if the mechanism involves modifications in brain morphology using the UK Biobank brain imaging cohort. This analysis shows that for several physiological factors, such as hypertension and obesity, a substantial part of the effect is mediated by changes in the brain structure. This work provides guidance to the practitioner from the formulation of a valid causal mediation problem, including the verification of the identification assumptions, to the choice of an adequate estimator.

Covariance-Adaptive Least-Squares Algorithm for Stochastic Combinatorial Semi-Bandits

We address the problem of stochastic combinatorial semi-bandits, where a player can select from P subsets of a set containing d base items. Most existing algorithms (e.g. CUCB, ESCB, OLS-UCB) require prior knowledge on the reward distribution, like an upper bound on a sub-Gaussian proxy-variance, which is hard to estimate tightly. In this work, we design a variance-adaptive version of OLS-UCB, relying on an online estimation of the covariance structure. Estimating the coefficients of a covariance matrix is much more manageable in practical settings and results in improved regret upper bounds compared to proxy variance-based algorithms. When covariance coefficients are all non-negative, we show that our approach efficiently leverages the semi-bandit feedback and provably outperforms bandit feedback approaches, not only in exponential regimes where P $\gg$ d but also when P $\le$ d, which is not straightforward from most existing analyses.

Sequential Counterfactual Risk Minimization

Counterfactual Risk Minimization (CRM) is a framework for dealing with the logged bandit feedback problem, where the goal is to improve a logging policy using offline data. In this paper, we explore the case where it is possible to deploy learned policies multiple times and acquire new data. We extend the CRM principle and its theory to this scenario, which we call "Sequential Counterfactual Risk Minimization (SCRM)." We introduce a novel counterfactual estimator and identify conditions that can improve the performance of CRM in terms of excess risk and regret rates, by using an analysis similar to restart strategies in accelerated optimization methods. We also provide an empirical evaluation of our method in both discrete and continuous action settings, and demonstrate the benefits of multiple deployments of CRM.

Nested bandits

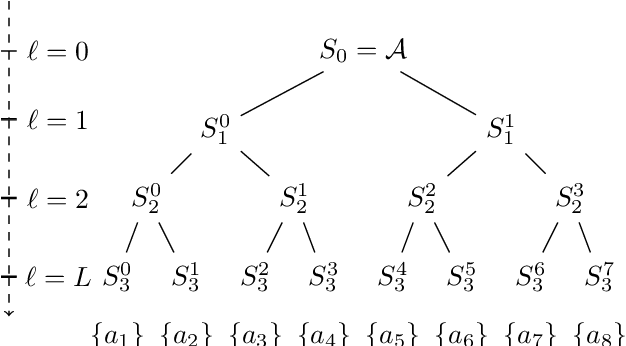
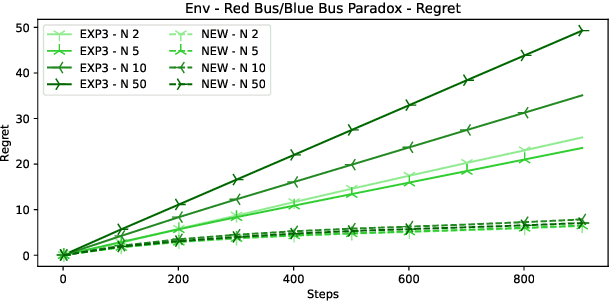
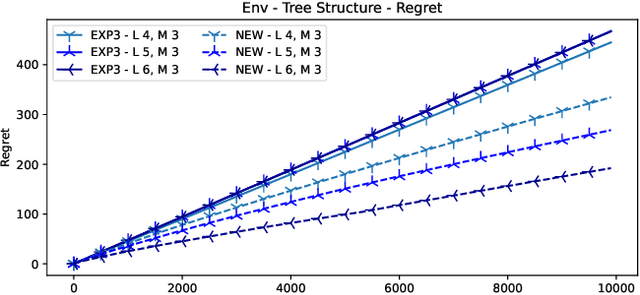
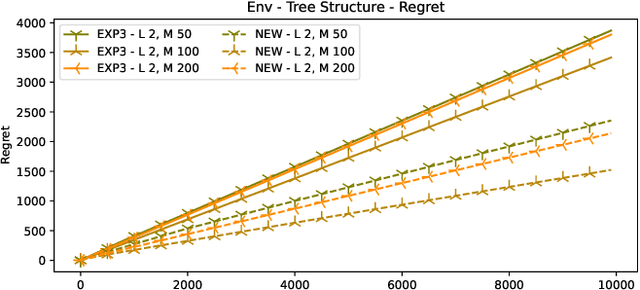
In many online decision processes, the optimizing agent is called to choose between large numbers of alternatives with many inherent similarities; in turn, these similarities imply closely correlated losses that may confound standard discrete choice models and bandit algorithms. We study this question in the context of nested bandits, a class of adversarial multi-armed bandit problems where the learner seeks to minimize their regret in the presence of a large number of distinct alternatives with a hierarchy of embedded (non-combinatorial) similarities. In this setting, optimal algorithms based on the exponential weights blueprint (like Hedge, EXP3, and their variants) may incur significant regret because they tend to spend excessive amounts of time exploring irrelevant alternatives with similar, suboptimal costs. To account for this, we propose a nested exponential weights (NEW) algorithm that performs a layered exploration of the learner's set of alternatives based on a nested, step-by-step selection method. In so doing, we obtain a series of tight bounds for the learner's regret showing that online learning problems with a high degree of similarity between alternatives can be resolved efficiently, without a red bus / blue bus paradox occurring.

Efficient Kernel UCB for Contextual Bandits

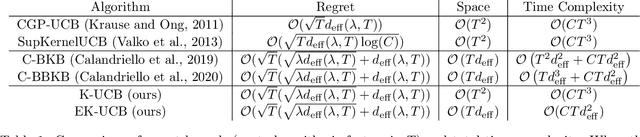
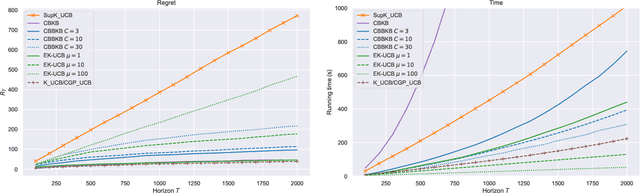
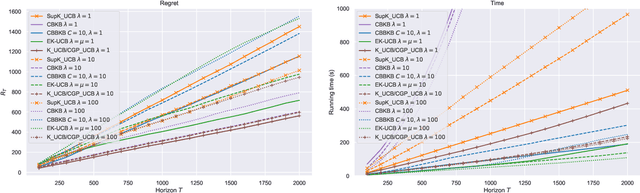
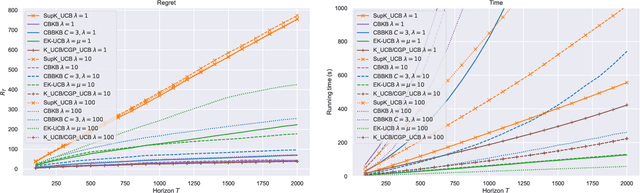
In this paper, we tackle the computational efficiency of kernelized UCB algorithms in contextual bandits. While standard methods require a O(CT^3) complexity where T is the horizon and the constant C is related to optimizing the UCB rule, we propose an efficient contextual algorithm for large-scale problems. Specifically, our method relies on incremental Nystrom approximations of the joint kernel embedding of contexts and actions. This allows us to achieve a complexity of O(CTm^2) where m is the number of Nystrom points. To recover the same regret as the standard kernelized UCB algorithm, m needs to be of order of the effective dimension of the problem, which is at most O(\sqrt(T)) and nearly constant in some cases.

Optimization Approaches for Counterfactual Risk Minimization with Continuous Actions

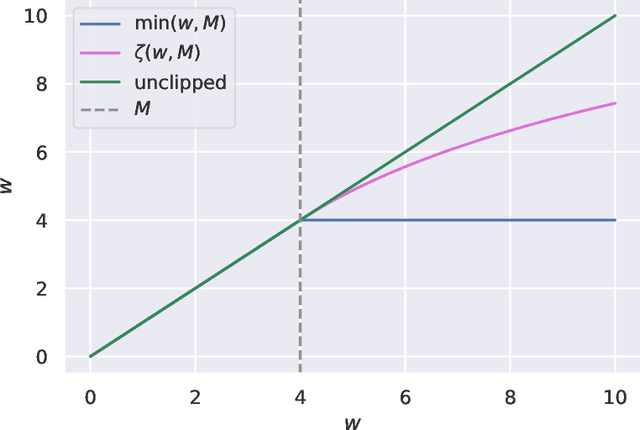
Counterfactual reasoning from logged data has become increasingly important for a large range of applications such as web advertising or healthcare. In this paper, we address the problem of counterfactual risk minimization for learning a stochastic policy with a continuous action space. Whereas previous works have mostly focused on deriving statistical estimators with importance sampling, we show that the optimization perspective is equally important for solving the resulting nonconvex optimization problems.Specifically, we demonstrate the benefits of proximal point algorithms and soft-clipping estimators which are more amenable to gradient-based optimization than classical hard clipping. We propose multiple synthetic, yet realistic, evaluation setups, and we release a new large-scale dataset based on web advertising data for this problem that is crucially missing public benchmarks.

Semi-Supervised Deep Learning for Abnormality Classification in Retinal Images

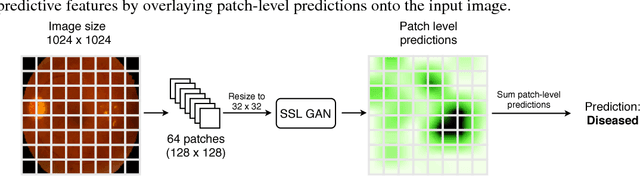
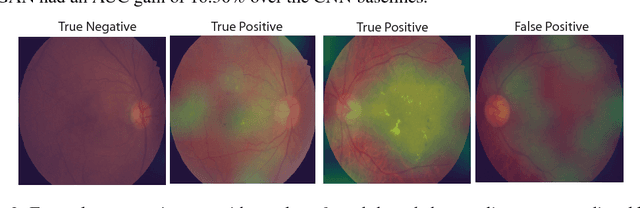
Supervised deep learning algorithms have enabled significant performance gains in medical image classification tasks. But these methods rely on large labeled datasets that require resource-intensive expert annotation. Semi-supervised generative adversarial network (GAN) approaches offer a means to learn from limited labeled data alongside larger unlabeled datasets, but have not been applied to discern fine-scale, sparse or localized features that define medical abnormalities. To overcome these limitations, we propose a patch-based semi-supervised learning approach and evaluate performance on classification of diabetic retinopathy from funduscopic images. Our semi-supervised approach achieves high AUC with just 10-20 labeled training images, and outperforms the supervised baselines by upto 15% when less than 30% of the training dataset is labeled. Further, our method implicitly enables interpretation of the SSL predictions. As this approach enables good accuracy, resolution and interpretability with lower annotation burden, it sets the pathway for scalable applications of deep learning in clinical imaging.

Adversarially Learned Anomaly Detection

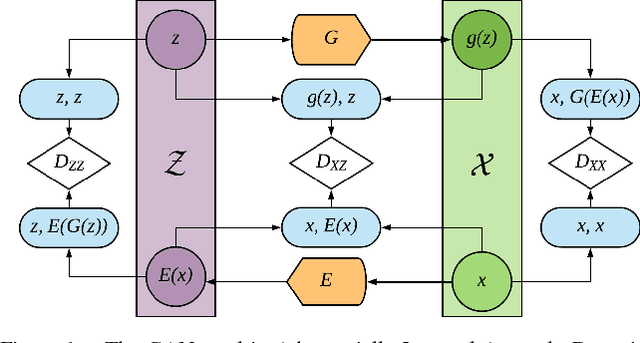
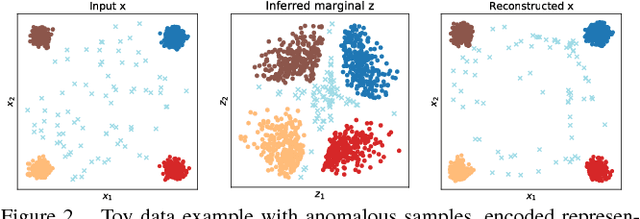
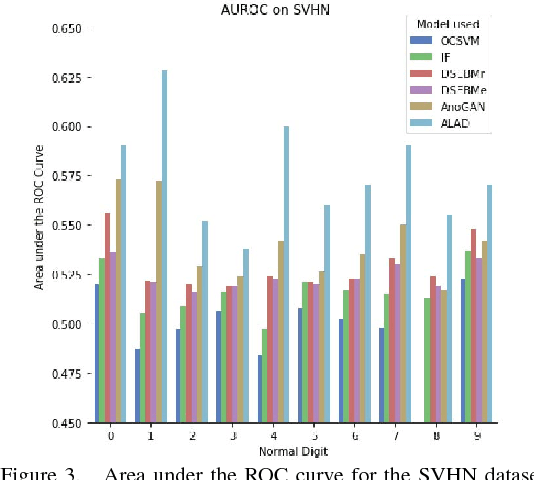
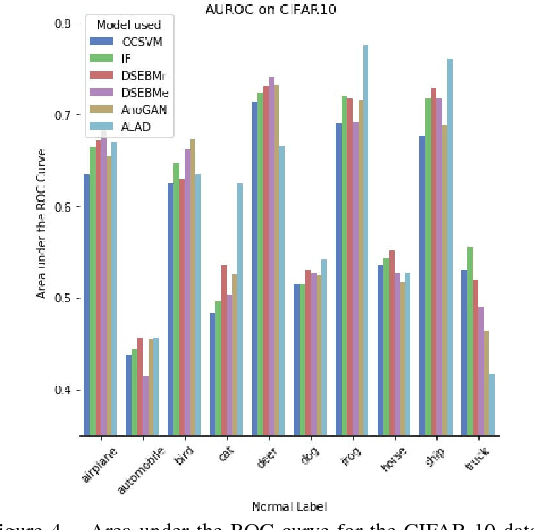
Anomaly detection is a significant and hence well-studied problem. However, developing effective anomaly detection methods for complex and high-dimensional data remains a challenge. As Generative Adversarial Networks (GANs) are able to model the complex high-dimensional distributions of real-world data, they offer a promising approach to address this challenge. In this work, we propose an anomaly detection method, Adversarially Learned Anomaly Detection (ALAD) based on bi-directional GANs, that derives adversarially learned features for the anomaly detection task. ALAD then uses reconstruction errors based on these adversarially learned features to determine if a data sample is anomalous. ALAD builds on recent advances to ensure data-space and latent-space cycle-consistencies and stabilize GAN training, which results in significantly improved anomaly detection performance. ALAD achieves state-of-the-art performance on a range of image and tabular datasets while being several hundred-fold faster at test time than the only published GAN-based method.

Optimistic mirror descent in saddle-point problems: Going the extra (gradient) mile

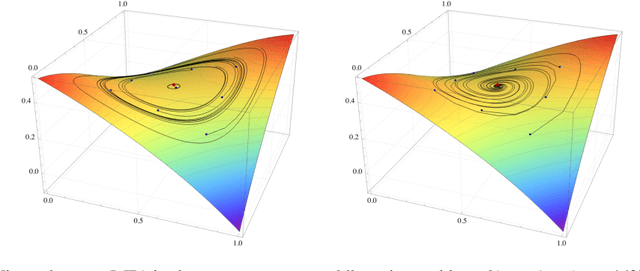
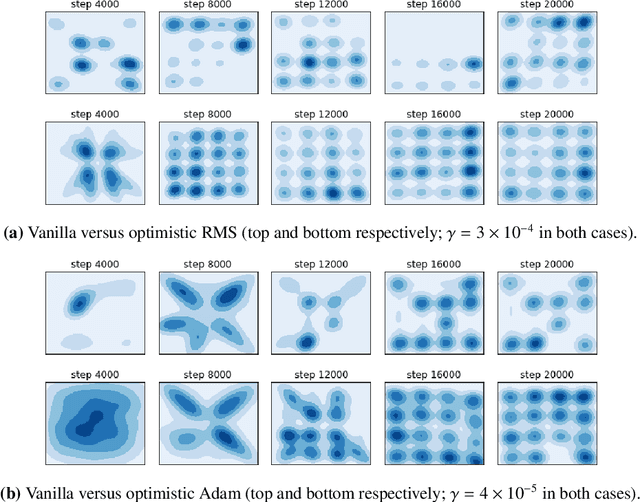
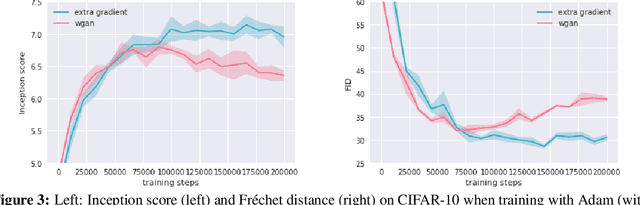
Owing to their connection with generative adversarial networks (GANs), saddle-point problems have recently attracted considerable interest in machine learning and beyond. By necessity, most theoretical guarantees revolve around convex-concave (or even linear) problems; however, making theoretical inroads towards efficient GAN training depends crucially on moving beyond this classic framework. To make piecemeal progress along these lines, we analyze the behavior of mirror descent (MD) in a class of non-monotone problems whose solutions coincide with those of a naturally associated variational inequality - a property which we call coherence. We first show that ordinary, "vanilla" MD converges under a strict version of this condition, but not otherwise; in particular, it may fail to converge even in bilinear models with a unique solution. We then show that this deficiency is mitigated by optimism: by taking an "extra-gradient" step, optimistic mirror descent (OMD) converges in all coherent problems. Our analysis generalizes and extends the results of Daskalakis et al. (2018) for optimistic gradient descent (OGD) in bilinear problems, and makes concrete headway for establishing convergence beyond convex-concave games. We also provide stochastic analogues of these results, and we validate our analysis by numerical experiments in a wide array of GAN models (including Gaussian mixture models, as well as the CelebA and CIFAR-10 datasets).