Exploring the Stratified Space Structure of an RL Game with the Volume Growth Transform

In this work, we explore the structure of the embedding space of a transformer model trained for playing a particular reinforcement learning (RL) game. Specifically, we investigate how a transformer-based Proximal Policy Optimization (PPO) model embeds visual inputs in a simple environment where an agent must collect "coins" while avoiding dynamic obstacles consisting of "spotlights." By adapting Robinson et al.'s study of the volume growth transform for LLMs to the RL setting, we find that the token embedding space for our visual coin collecting game is also not a manifold, and is better modeled as a stratified space, where local dimension can vary from point to point. We further strengthen Robinson's method by proving that fairly general volume growth curves can be realized by stratified spaces. Finally, we carry out an analysis that suggests that as an RL agent acts, its latent representation alternates between periods of low local dimension, while following a fixed sub-strategy, and bursts of high local dimension, where the agent achieves a sub-goal (e.g., collecting an object) or where the environmental complexity increases (e.g., more obstacles appear). Consequently, our work suggests that the distribution of dimensions in a stratified latent space may provide a new geometric indicator of complexity for RL games.

Position Paper: Challenges and Opportunities in Topological Deep Learning

Topological deep learning (TDL) is a rapidly evolving field that uses topological features to understand and design deep learning models. This paper posits that TDL may complement graph representation learning and geometric deep learning by incorporating topological concepts, and can thus provide a natural choice for various machine learning settings. To this end, this paper discusses open problems in TDL, ranging from practical benefits to theoretical foundations. For each problem, it outlines potential solutions and future research opportunities. At the same time, this paper serves as an invitation to the scientific community to actively participate in TDL research to unlock the potential of this emerging field.

Algebraic and Geometric Models for Space Networking

In this paper we introduce some new algebraic and geometric perspectives on networked space communications. Our main contribution is a novel definition of a time-varying graph (TVG), defined in terms of a matrix with values in subsets of the real line P(R). We leverage semi-ring properties of P(R) to model multi-hop communication in a TVG using matrix multiplication and a truncated Kleene star. This leads to novel statistics on the communication capacity of TVGs called lifetime curves, which we generate for large samples of randomly chosen STARLINK satellites, whose connectivity is modeled over day-long simulations. Determining when a large subsample of STARLINK is temporally strongly connected is further analyzed using novel metrics introduced here that are inspired by topological data analysis (TDA). To better model networking scenarios between the Earth and Mars, we introduce various semi-rings capable of modeling propagation delay as well as protocols common to Delay Tolerant Networking (DTN), such as store-and-forward. Finally, we illustrate the applicability of zigzag persistence for featurizing different space networks and demonstrate the efficacy of K-Nearest Neighbors (KNN) classification for distinguishing Earth-Mars and Earth-Moon satellite systems using time-varying topology alone.

The Universal $\ell^p$-Metric on Merge Trees

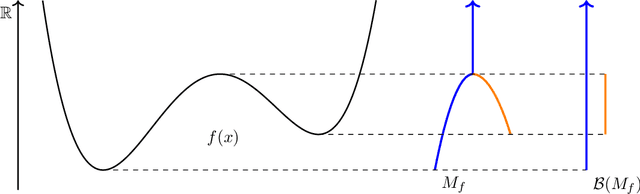
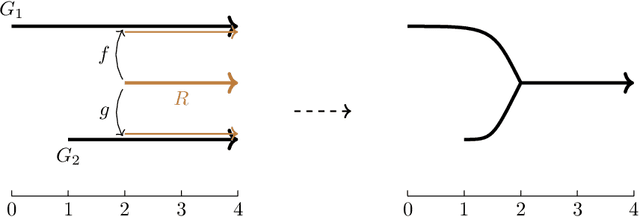
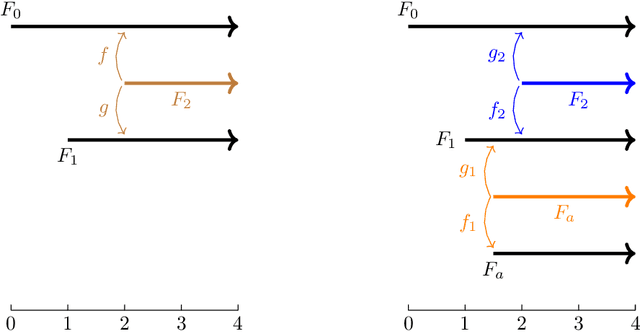
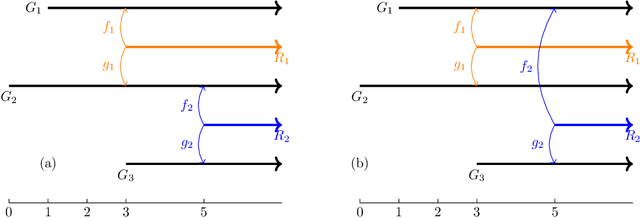
Adapting a definition given by Bjerkevik and Lesnick for multiparameter persistence modules, we introduce an $\ell^p$-type extension of the interleaving distance on merge trees. We show that our distance is a metric, and that it upper-bounds the $p$-Wasserstein distance between the associated barcodes. For each $p\in[1,\infty]$, we prove that this distance is stable with respect to cellular sublevel filtrations and that it is the universal (i.e., largest) distance satisfying this stability property. In the $p=\infty$ case, this gives a novel proof of universality for the interleaving distance on merge trees.