Physics Informed Constrained Learning of Dynamics from Static Data

A physics-informed neural network (PINN) models the dynamics of a system by integrating the governing physical laws into the architecture of a neural network. By enforcing physical laws as constraints, PINN overcomes challenges with data scarsity and potentially high dimensionality. Existing PINN frameworks rely on fully observed time-course data, the acquisition of which could be prohibitive for many systems. In this study, we developed a new PINN learning paradigm, namely Constrained Learning, that enables the approximation of first-order derivatives or motions using non-time course or partially observed data. Computational principles and a general mathematical formulation of Constrained Learning were developed. We further introduced MPOCtrL (Message Passing Optimization-based Constrained Learning) an optimization approach tailored for the Constrained Learning framework that strives to balance the fitting of physical models and observed data. Its code is available at github link: https://github.com/ptdang1001/MPOCtrL Experiments on synthetic and real-world data demonstrated that MPOCtrL can effectively detect the nonlinear dependency between observed data and the underlying physical properties of the system. In particular, on the task of metabolic flux analysis, MPOCtrL outperforms all existing data-driven flux estimators.

Spatially and Robustly Hybrid Mixture Regression Model for Inference of Spatial Dependence

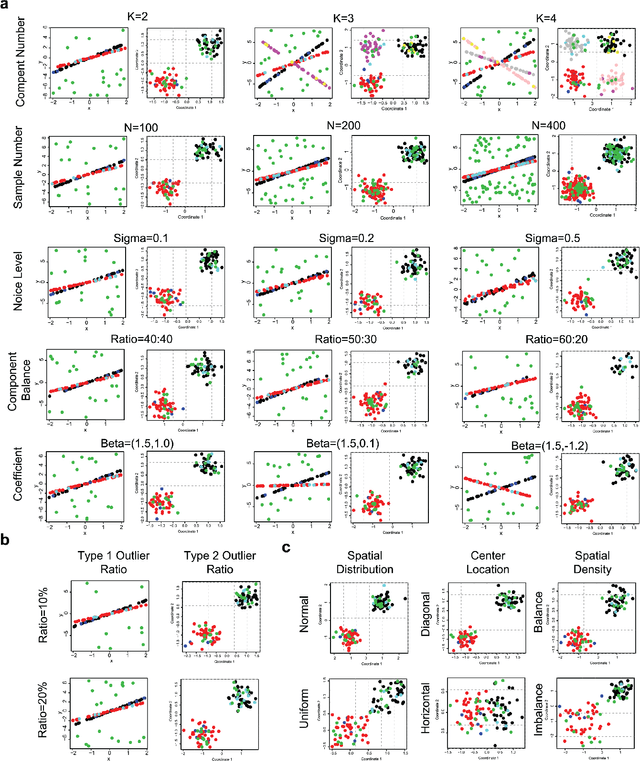
In this paper, we propose a Spatial Robust Mixture Regression model to investigate the relationship between a response variable and a set of explanatory variables over the spatial domain, assuming that the relationships may exhibit complex spatially dynamic patterns that cannot be captured by constant regression coefficients. Our method integrates the robust finite mixture Gaussian regression model with spatial constraints, to simultaneously handle the spatial nonstationarity, local homogeneity, and outlier contaminations. Compared with existing spatial regression models, our proposed model assumes the existence a few distinct regression models that are estimated based on observations that exhibit similar response-predictor relationships. As such, the proposed model not only accounts for nonstationarity in the spatial trend, but also clusters observations into a few distinct and homogenous groups. This provides an advantage on interpretation with a few stationary sub-processes identified that capture the predominant relationships between response and predictor variables. Moreover, the proposed method incorporates robust procedures to handle contaminations from both regression outliers and spatial outliers. By doing so, we robustly segment the spatial domain into distinct local regions with similar regression coefficients, and sporadic locations that are purely outliers. Rigorous statistical hypothesis testing procedure has been designed to test the significance of such segmentation. Experimental results on many synthetic and real-world datasets demonstrate the robustness, accuracy, and effectiveness of our proposed method, compared with other robust finite mixture regression, spatial regression and spatial segmentation methods.