Stepping on the Edge: Curvature Aware Learning Rate Tuners

Curvature information -- particularly, the largest eigenvalue of the loss Hessian, known as the sharpness -- often forms the basis for learning rate tuners. However, recent work has shown that the curvature information undergoes complex dynamics during training, going from a phase of increasing sharpness to eventual stabilization. We analyze the closed-loop feedback effect between learning rate tuning and curvature. We find that classical learning rate tuners may yield greater one-step loss reduction, yet they ultimately underperform in the long term when compared to constant learning rates in the full batch regime. These models break the stabilization of the sharpness, which we explain using a simplified model of the joint dynamics of the learning rate and the curvature. To further investigate these effects, we introduce a new learning rate tuning method, Curvature Dynamics Aware Tuning (CDAT), which prioritizes long term curvature stabilization over instantaneous progress on the objective. In the full batch regime, CDAT shows behavior akin to prefixed warm-up schedules on deep learning objectives, outperforming tuned constant learning rates. In the mini batch regime, we observe that stochasticity introduces confounding effects that explain the previous success of some learning rate tuners at appropriate batch sizes. Our findings highlight the critical role of understanding the joint dynamics of the learning rate and curvature, beyond greedy minimization, to diagnose failures and design effective adaptive learning rate tuners.

Rapid training of deep neural networks without skip connections or normalization layers using Deep Kernel Shaping

Using an extended and formalized version of the Q/C map analysis of Poole et al. (2016), along with Neural Tangent Kernel theory, we identify the main pathologies present in deep networks that prevent them from training fast and generalizing to unseen data, and show how these can be avoided by carefully controlling the "shape" of the network's initialization-time kernel function. We then develop a method called Deep Kernel Shaping (DKS), which accomplishes this using a combination of precise parameter initialization, activation function transformations, and small architectural tweaks, all of which preserve the model class. In our experiments we show that DKS enables SGD training of residual networks without normalization layers on Imagenet and CIFAR-10 classification tasks at speeds comparable to standard ResNetV2 and Wide-ResNet models, with only a small decrease in generalization performance. And when using K-FAC as the optimizer, we achieve similar results for networks without skip connections. Our results apply for a large variety of activation functions, including those which traditionally perform very badly, such as the logistic sigmoid. In addition to DKS, we contribute a detailed analysis of skip connections, normalization layers, special activation functions like RELU and SELU, and various initialization schemes, explaining their effectiveness as alternative (and ultimately incomplete) ways of "shaping" the network's initialization-time kernel.

Gradient Forward-Propagation for Large-Scale Temporal Video Modelling

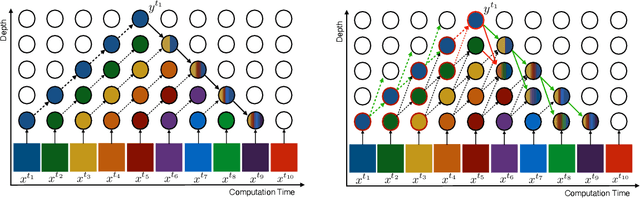
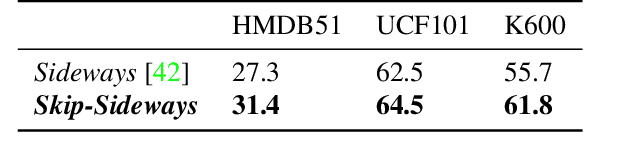
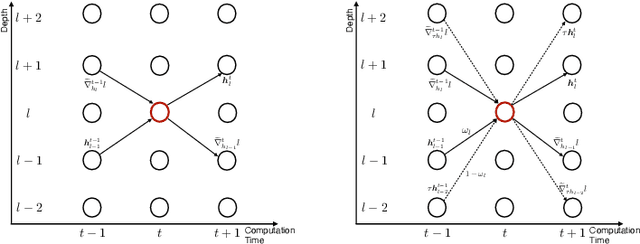
How can neural networks be trained on large-volume temporal data efficiently? To compute the gradients required to update parameters, backpropagation blocks computations until the forward and backward passes are completed. For temporal signals, this introduces high latency and hinders real-time learning. It also creates a coupling between consecutive layers, which limits model parallelism and increases memory consumption. In this paper, we build upon Sideways, which avoids blocking by propagating approximate gradients forward in time, and we propose mechanisms for temporal integration of information based on different variants of skip connections. We also show how to decouple computation and delegate individual neural modules to different devices, allowing distributed and parallel training. The proposed Skip-Sideways achieves low latency training, model parallelism, and, importantly, is capable of extracting temporal features, leading to more stable training and improved performance on real-world action recognition video datasets such as HMDB51, UCF101, and the large-scale Kinetics-600. Finally, we also show that models trained with Skip-Sideways generate better future frames than Sideways models, and hence they can better utilize motion cues.

Sideways: Depth-Parallel Training of Video Models

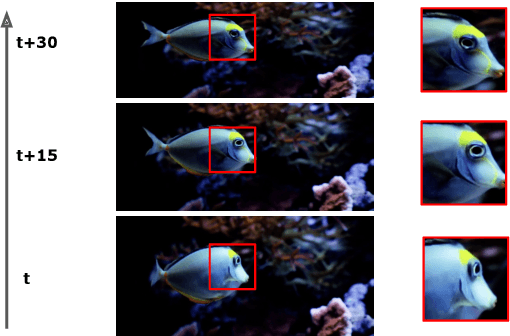
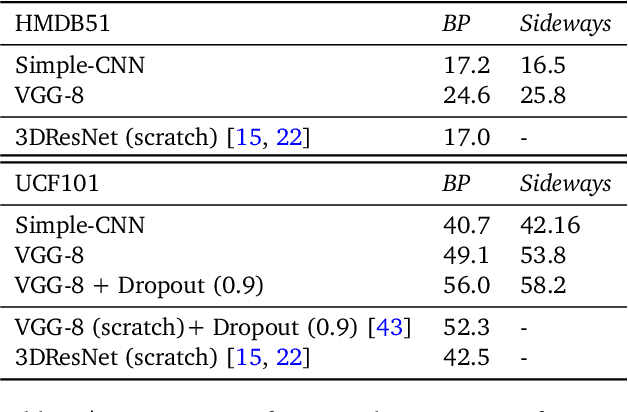
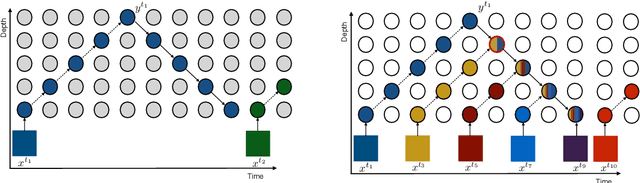
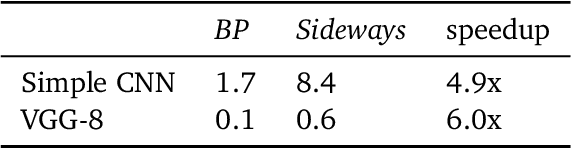
We propose Sideways, an approximate backpropagation scheme for training video models. In standard backpropagation, the gradients and activations at every computation step through the model are temporally synchronized. The forward activations need to be stored until the backward pass is executed, preventing inter-layer (depth) parallelization. However, can we leverage smooth, redundant input streams such as videos to develop a more efficient training scheme? Here, we explore an alternative to backpropagation; we overwrite network activations whenever new ones, i.e., from new frames, become available. Such a more gradual accumulation of information from both passes breaks the precise correspondence between gradients and activations, leading to theoretically more noisy weight updates. Counter-intuitively, we show that Sideways training of deep convolutional video networks not only still converges, but can also potentially exhibit better generalization compared to standard synchronized backpropagation.

Verification of Non-Linear Specifications for Neural Networks

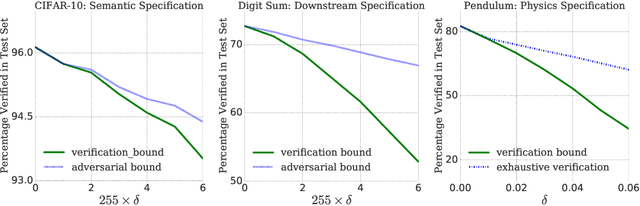
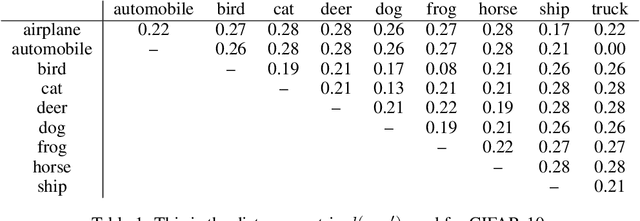
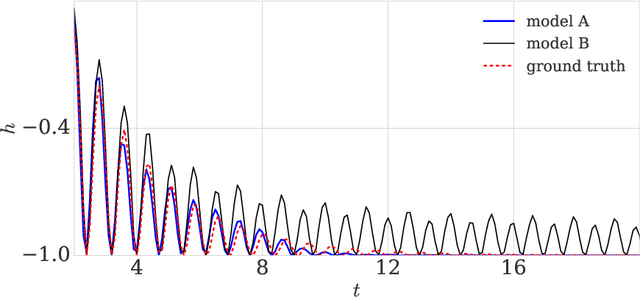
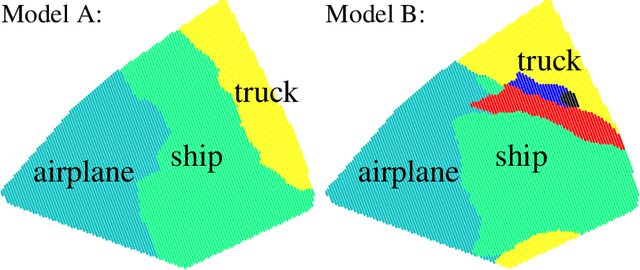
Prior work on neural network verification has focused on specifications that are linear functions of the output of the network, e.g., invariance of the classifier output under adversarial perturbations of the input. In this paper, we extend verification algorithms to be able to certify richer properties of neural networks. To do this we introduce the class of convex-relaxable specifications, which constitute nonlinear specifications that can be verified using a convex relaxation. We show that a number of important properties of interest can be modeled within this class, including conservation of energy in a learned dynamics model of a physical system; semantic consistency of a classifier's output labels under adversarial perturbations and bounding errors in a system that predicts the summation of handwritten digits. Our experimental evaluation shows that our method is able to effectively verify these specifications. Moreover, our evaluation exposes the failure modes in models which cannot be verified to satisfy these specifications. Thus, emphasizing the importance of training models not just to fit training data but also to be consistent with specifications.

Distilling Policy Distillation

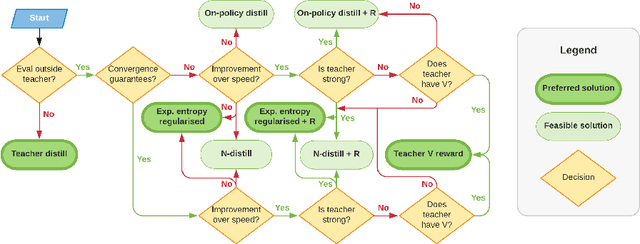
The transfer of knowledge from one policy to another is an important tool in Deep Reinforcement Learning. This process, referred to as distillation, has been used to great success, for example, by enhancing the optimisation of agents, leading to stronger performance faster, on harder domains [26, 32, 5, 8]. Despite the widespread use and conceptual simplicity of distillation, many different formulations are used in practice, and the subtle variations between them can often drastically change the performance and the resulting objective that is being optimised. In this work, we rigorously explore the entire landscape of policy distillation, comparing the motivations and strengths of each variant through theoretical and empirical analysis. Our results point to three distillation techniques, that are preferred depending on specifics of the task. Specifically a newly proposed expected entropy regularised distillation allows for quicker learning in a wide range of situations, while still guaranteeing convergence.

Strength in Numbers: Trading-off Robustness and Computation via Adversarially-Trained Ensembles

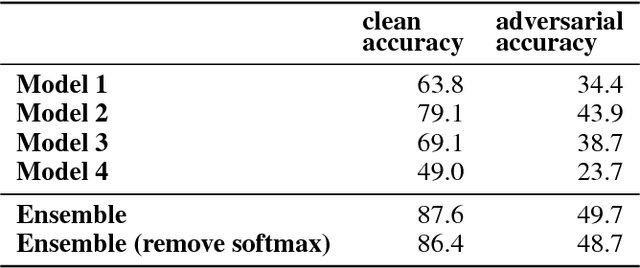
While deep learning has led to remarkable results on a number of challenging problems, researchers have discovered a vulnerability of neural networks in adversarial settings, where small but carefully chosen perturbations to the input can make the models produce extremely inaccurate outputs. This makes these models particularly unsuitable for safety-critical application domains (e.g. self-driving cars) where robustness is extremely important. Recent work has shown that augmenting training with adversarially generated data provides some degree of robustness against test-time attacks. In this paper we investigate how this approach scales as we increase the computational budget given to the defender. We show that increasing the number of parameters in adversarially-trained models increases their robustness, and in particular that ensembling smaller models while adversarially training the entire ensemble as a single model is a more efficient way of spending said budget than simply using a larger single model. Crucially, we show that it is the adversarial training of the ensemble, rather than the ensembling of adversarially trained models, which provides robustness.

Local minima in training of neural networks

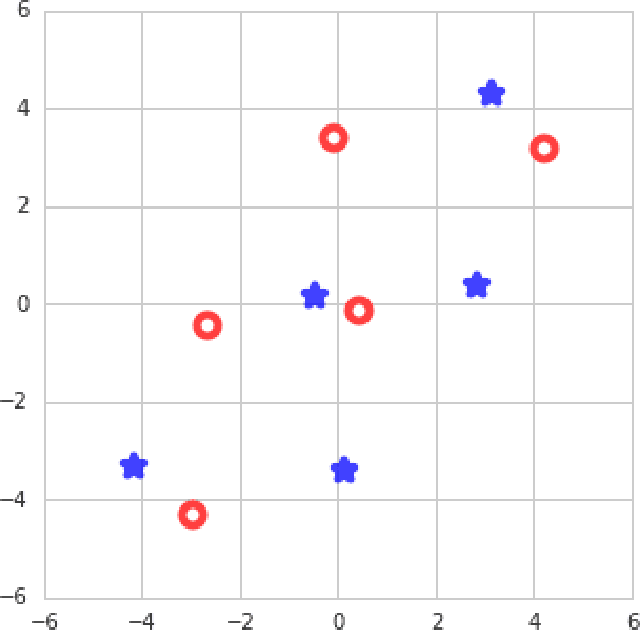
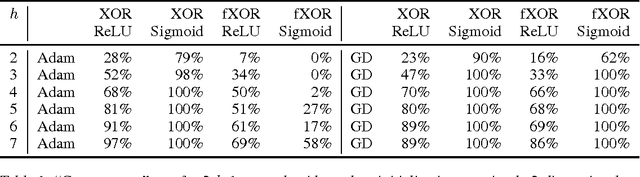
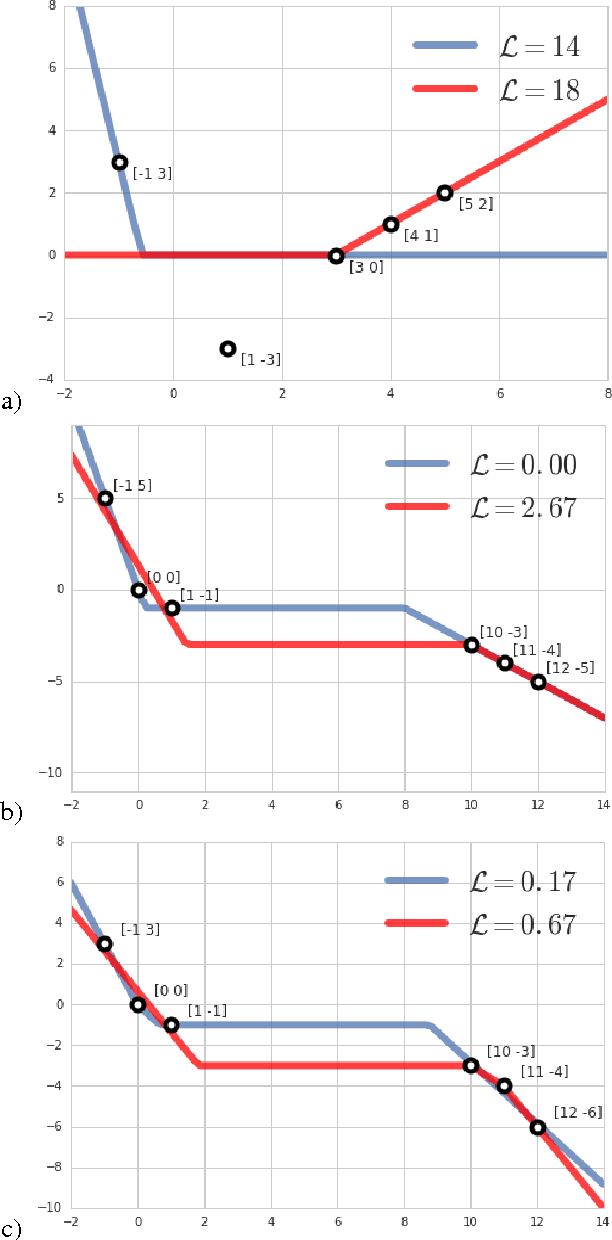
There has been a lot of recent interest in trying to characterize the error surface of deep models. This stems from a long standing question. Given that deep networks are highly nonlinear systems optimized by local gradient methods, why do they not seem to be affected by bad local minima? It is widely believed that training of deep models using gradient methods works so well because the error surface either has no local minima, or if they exist they need to be close in value to the global minimum. It is known that such results hold under very strong assumptions which are not satisfied by real models. In this paper we present examples showing that for such theorem to be true additional assumptions on the data, initialization schemes and/or the model classes have to be made. We look at the particular case of finite size datasets. We demonstrate that in this scenario one can construct counter-examples (datasets or initialization schemes) when the network does become susceptible to bad local minima over the weight space.