From Invariant Representations to Invariant Data: Provable Robustness to Spurious Correlations via Noisy Counterfactual Matching

Spurious correlations can cause model performance to degrade in new environments. Prior causality-inspired works aim to learn invariant representations (e.g., IRM) but typically underperform empirical risk minimization (ERM). Recent alternatives improve robustness by leveraging test-time data, but such data may be unavailable in practice. To address these issues, we take a data-centric approach by leveraging invariant data pairs, pairs of samples that would have the same prediction with the optimally robust classifier. We prove that certain counterfactual pairs will naturally satisfy this invariance property and introduce noisy counterfactual matching (NCM), a simple constraint-based method for leveraging invariant pairs for enhanced robustness, even with a small set of noisy pairs-in the ideal case, each pair can eliminate one spurious feature. For linear causal models, we prove that the test domain error can be upper bounded by the in-domain error and a term that depends on the counterfactuals' diversity and quality. We validate on a synthetic dataset and demonstrate on real-world benchmarks that linear probing on a pretrained backbone improves robustness.

Distributed Sparse Regression via Penalization

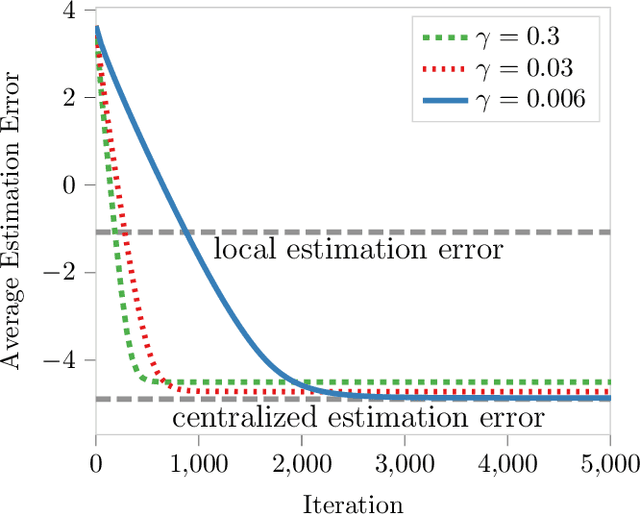
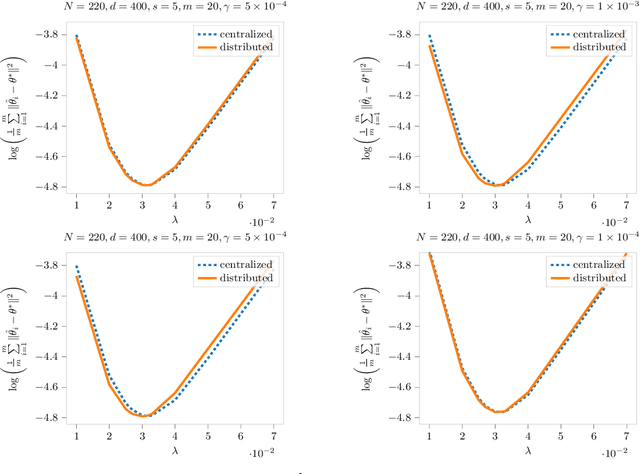
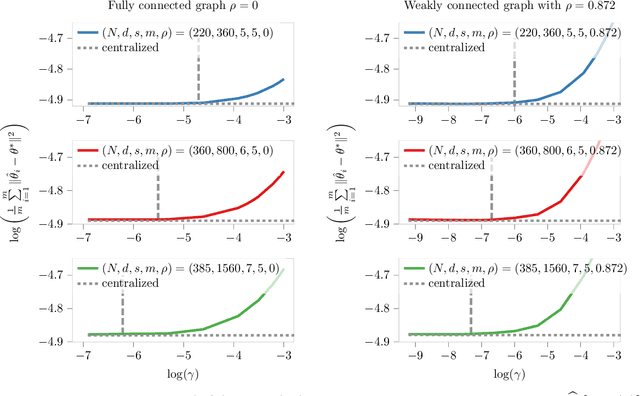
We study sparse linear regression over a network of agents, modeled as an undirected graph (with no centralized node). The estimation problem is formulated as the minimization of the sum of the local LASSO loss functions plus a quadratic penalty of the consensus constraint -- the latter being instrumental to obtain distributed solution methods. While penalty-based consensus methods have been extensively studied in the optimization literature, their statistical and computational guarantees in the high dimensional setting remain unclear. This work provides an answer to this open problem. Our contribution is two-fold. First, we establish statistical consistency of the estimator: under a suitable choice of the penalty parameter, the optimal solution of the penalized problem achieves near optimal minimax rate $\mathcal{O}(s \log d/N)$ in $\ell_2$-loss, where $s$ is the sparsity value, $d$ is the ambient dimension, and $N$ is the total sample size in the network -- this matches centralized sample rates. Second, we show that the proximal-gradient algorithm applied to the penalized problem, which naturally leads to distributed implementations, converges linearly up to a tolerance of the order of the centralized statistical error -- the rate scales as $\mathcal{O}(d)$, revealing an unavoidable speed-accuracy dilemma.Numerical results demonstrate the tightness of the derived sample rate and convergence rate scalings.