Non-Local Graph-Based Prediction For Reversible Data Hiding In Images

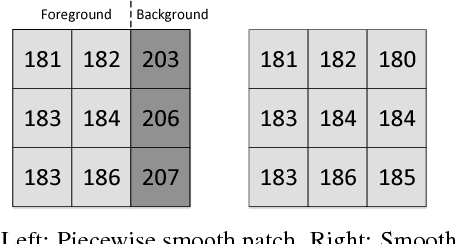
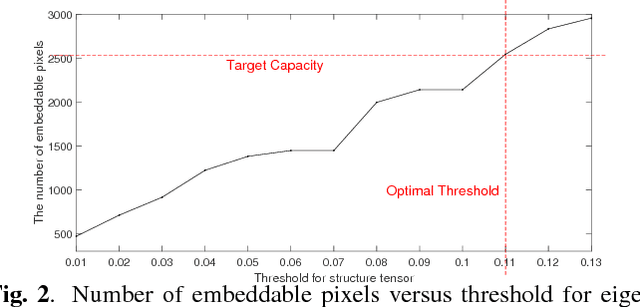
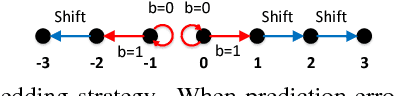
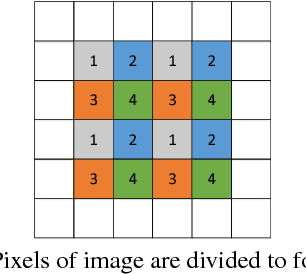
Reversible data hiding (RDH) is desirable in applications where both the hidden message and the cover medium need to be recovered without loss. Among many RDH approaches is prediction-error expansion (PEE), containing two steps: i) prediction of a target pixel value, and ii) embedding according to the value of prediction-error. In general, higher prediction performance leads to larger embedding capacity and/or lower signal distortion. Leveraging on recent advances in graph signal processing (GSP), we pose pixel prediction as a graph-signal restoration problem, where the appropriate edge weights of the underlying graph are computed using a similar patch searched in a semi-local neighborhood. Specifically, for each candidate patch, we first examine eigenvalues of its structure tensor to estimate its local smoothness. If sufficiently smooth, we pose a maximum a posteriori (MAP) problem using either a quadratic Laplacian regularizer or a graph total variation (GTV) term as signal prior. While the MAP problem using the first prior has a closed-form solution, we design an efficient algorithm for the second prior using alternating direction method of multipliers (ADMM) with nested proximal gradient descent. Experimental results show that with better quality GSP-based prediction, at low capacity the visual quality of the embedded image exceeds state-of-the-art methods noticeably.

Blind Image Deblurring via Reweighted Graph Total Variation

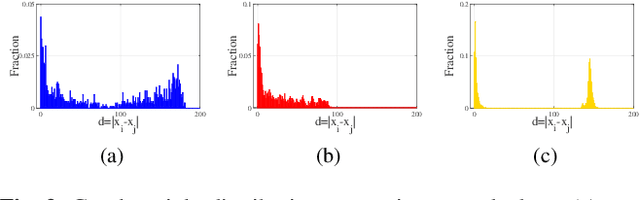
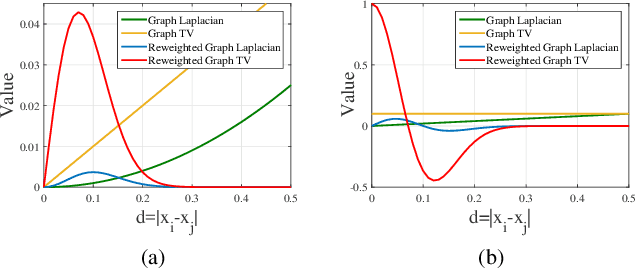
Blind image deblurring, i.e., deblurring without knowledge of the blur kernel, is a highly ill-posed problem. The problem can be solved in two parts: i) estimate a blur kernel from the blurry image, and ii) given estimated blur kernel, de-convolve blurry input to restore the target image. In this paper, by interpreting an image patch as a signal on a weighted graph, we first argue that a skeleton image---a proxy that retains the strong gradients of the target but smooths out the details---can be used to accurately estimate the blur kernel and has a unique bi-modal edge weight distribution. We then design a reweighted graph total variation (RGTV) prior that can efficiently promote bi-modal edge weight distribution given a blurry patch. However, minimizing a blind image deblurring objective with RGTV results in a non-convex non-differentiable optimization problem. We propose a fast algorithm that solves for the skeleton image and the blur kernel alternately. Finally with the computed blur kernel, recent non-blind image deblurring algorithms can be applied to restore the target image. Experimental results show that our algorithm can robustly estimate the blur kernel with large kernel size, and the reconstructed sharp image is competitive against the state-of-the-art methods.

Graph Laplacian Regularization for Image Denoising: Analysis in the Continuous Domain

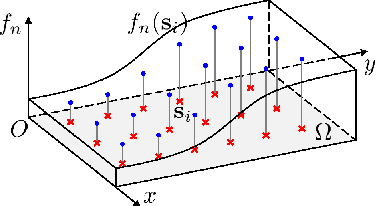
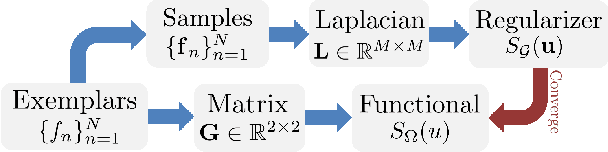
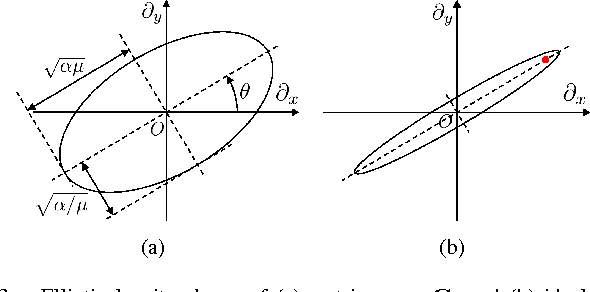
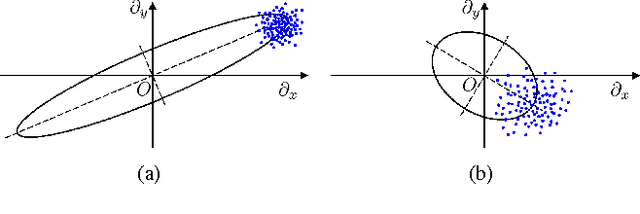
Inverse imaging problems are inherently under-determined, and hence it is important to employ appropriate image priors for regularization. One recent popular prior---the graph Laplacian regularizer---assumes that the target pixel patch is smooth with respect to an appropriately chosen graph. However, the mechanisms and implications of imposing the graph Laplacian regularizer on the original inverse problem are not well understood. To address this problem, in this paper we interpret neighborhood graphs of pixel patches as discrete counterparts of Riemannian manifolds and perform analysis in the continuous domain, providing insights into several fundamental aspects of graph Laplacian regularization for image denoising. Specifically, we first show the convergence of the graph Laplacian regularizer to a continuous-domain functional, integrating a norm measured in a locally adaptive metric space. Focusing on image denoising, we derive an optimal metric space assuming non-local self-similarity of pixel patches, leading to an optimal graph Laplacian regularizer for denoising in the discrete domain. We then interpret graph Laplacian regularization as an anisotropic diffusion scheme to explain its behavior during iterations, e.g., its tendency to promote piecewise smooth signals under certain settings. To verify our analysis, an iterative image denoising algorithm is developed. Experimental results show that our algorithm performs competitively with state-of-the-art denoising methods such as BM3D for natural images, and outperforms them significantly for piecewise smooth images.

Robust Semi-Supervised Graph Classifier Learning with Negative Edge Weights

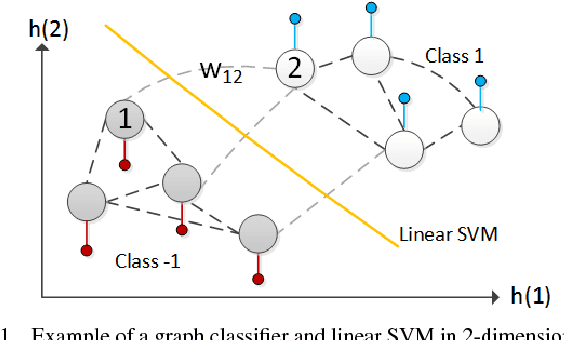
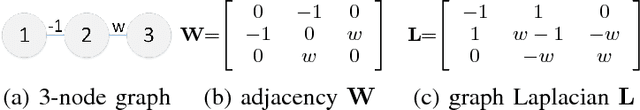
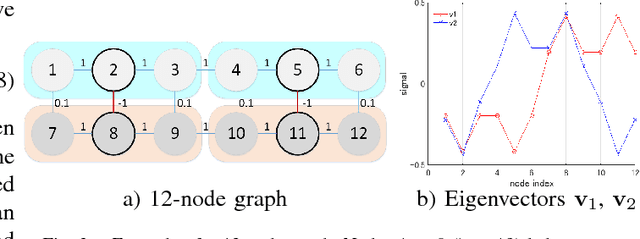
In a semi-supervised learning scenario, (possibly noisy) partially observed labels are used as input to train a classifier, in order to assign labels to unclassified samples. In this paper, we study this classifier learning problem from a graph signal processing (GSP) perspective. Specifically, by viewing a binary classifier as a piecewise constant graph-signal in a high-dimensional feature space, we cast classifier learning as a signal restoration problem via a classical maximum a posteriori (MAP) formulation. Unlike previous graph-signal restoration works, we consider in addition edges with negative weights that signify anti-correlation between samples. One unfortunate consequence is that the graph Laplacian matrix $\mathbf{L}$ can be indefinite, and previously proposed graph-signal smoothness prior $\mathbf{x}^T \mathbf{L} \mathbf{x}$ for candidate signal $\mathbf{x}$ can lead to pathological solutions. In response, we derive an optimal perturbation matrix $\boldsymbol{\Delta}$ - based on a fast lower-bound computation of the minimum eigenvalue of $\mathbf{L}$ via a novel application of the Haynsworth inertia additivity formula---so that $\mathbf{L} + \boldsymbol{\Delta}$ is positive semi-definite, resulting in a stable signal prior. Further, instead of forcing a hard binary decision for each sample, we define the notion of generalized smoothness on graph that promotes ambiguity in the classifier signal. Finally, we propose an algorithm based on iterative reweighted least squares (IRLS) that solves the posed MAP problem efficiently. Extensive simulation results show that our proposed algorithm outperforms both SVM variants and graph-based classifiers using positive-edge graphs noticeably.

Joint Denoising / Compression of Image Contours via Shape Prior and Context Tree

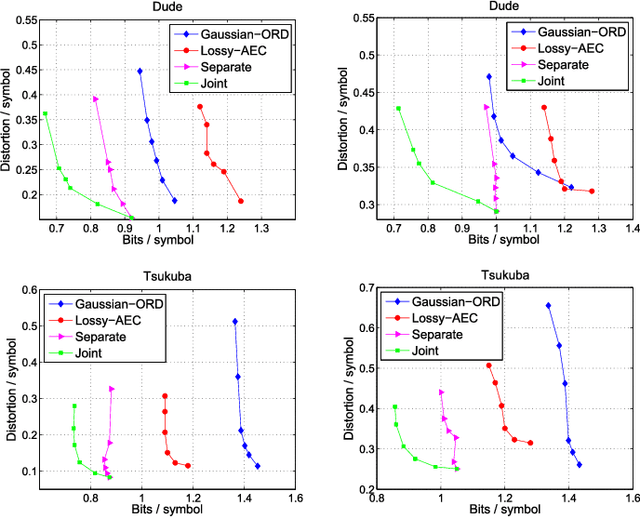
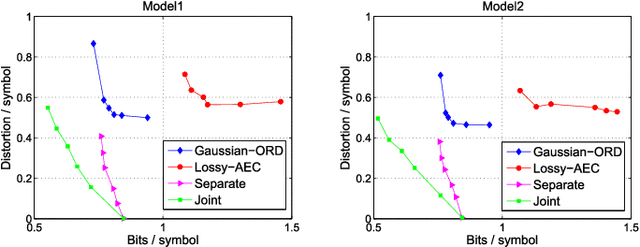
With the advent of depth sensing technologies, the extraction of object contours in images---a common and important pre-processing step for later higher-level computer vision tasks like object detection and human action recognition---has become easier. However, acquisition noise in captured depth images means that detected contours suffer from unavoidable errors. In this paper, we propose to jointly denoise and compress detected contours in an image for bandwidth-constrained transmission to a client, who can then carry out aforementioned application-specific tasks using the decoded contours as input. We first prove theoretically that in general a joint denoising / compression approach can outperform a separate two-stage approach that first denoises then encodes contours lossily. Adopting a joint approach, we first propose a burst error model that models typical errors encountered in an observed string y of directional edges. We then formulate a rate-constrained maximum a posteriori (MAP) problem that trades off the posterior probability p(x'|y) of an estimated string x' given y with its code rate R(x'). We design a dynamic programming (DP) algorithm that solves the posed problem optimally, and propose a compact context representation called total suffix tree (TST) that can reduce complexity of the algorithm dramatically. Experimental results show that our joint denoising / compression scheme outperformed a competing separate scheme in rate-distortion performance noticeably.

Random Walk Graph Laplacian based Smoothness Prior for Soft Decoding of JPEG Images

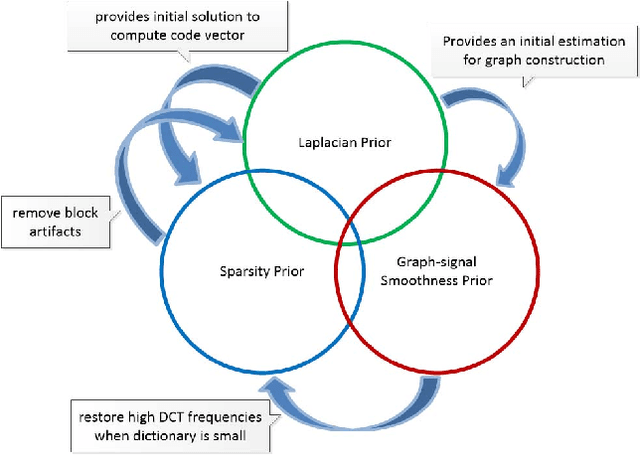
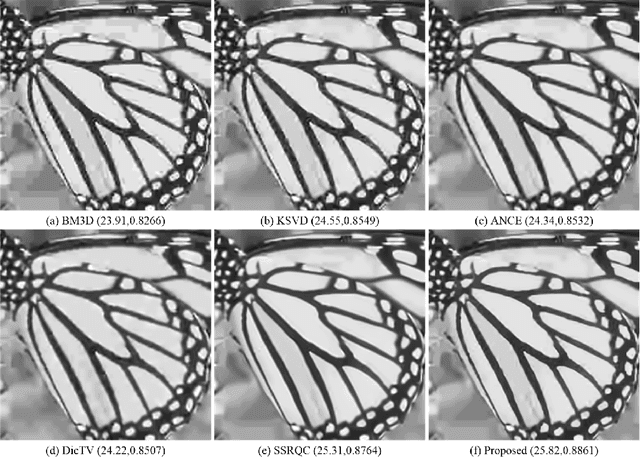
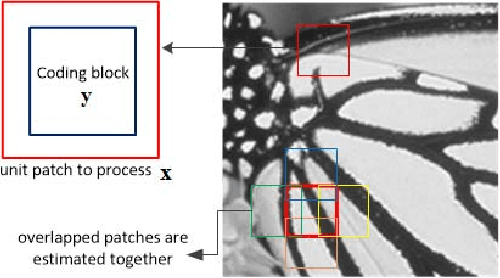
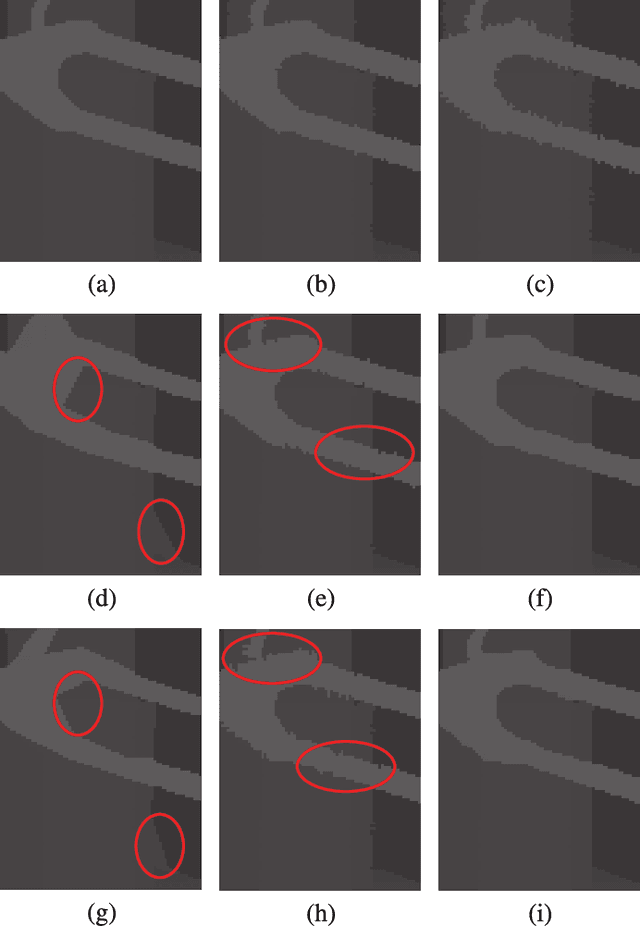
Given the prevalence of JPEG compressed images, optimizing image reconstruction from the compressed format remains an important problem. Instead of simply reconstructing a pixel block from the centers of indexed DCT coefficient quantization bins (hard decoding), soft decoding reconstructs a block by selecting appropriate coefficient values within the indexed bins with the help of signal priors. The challenge thus lies in how to define suitable priors and apply them effectively. In this paper, we combine three image priors---Laplacian prior for DCT coefficients, sparsity prior and graph-signal smoothness prior for image patches---to construct an efficient JPEG soft decoding algorithm. Specifically, we first use the Laplacian prior to compute a minimum mean square error (MMSE) initial solution for each code block. Next, we show that while the sparsity prior can reduce block artifacts, limiting the size of the over-complete dictionary (to lower computation) would lead to poor recovery of high DCT frequencies. To alleviate this problem, we design a new graph-signal smoothness prior (desired signal has mainly low graph frequencies) based on the left eigenvectors of the random walk graph Laplacian matrix (LERaG). Compared to previous graph-signal smoothness priors, LERaG has desirable image filtering properties with low computation overhead. We demonstrate how LERaG can facilitate recovery of high DCT frequencies of a piecewise smooth (PWS) signal via an interpretation of low graph frequency components as relaxed solutions to normalized cut in spectral clustering. Finally, we construct a soft decoding algorithm using the three signal priors with appropriate prior weights. Experimental results show that our proposal outperforms state-of-the-art soft decoding algorithms in both objective and subjective evaluations noticeably.

Precision Enhancement of 3D Surfaces from Multiple Compressed Depth Maps

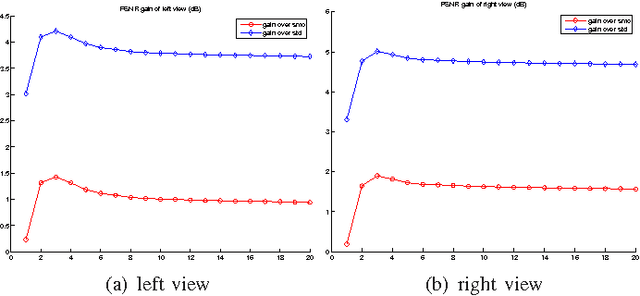
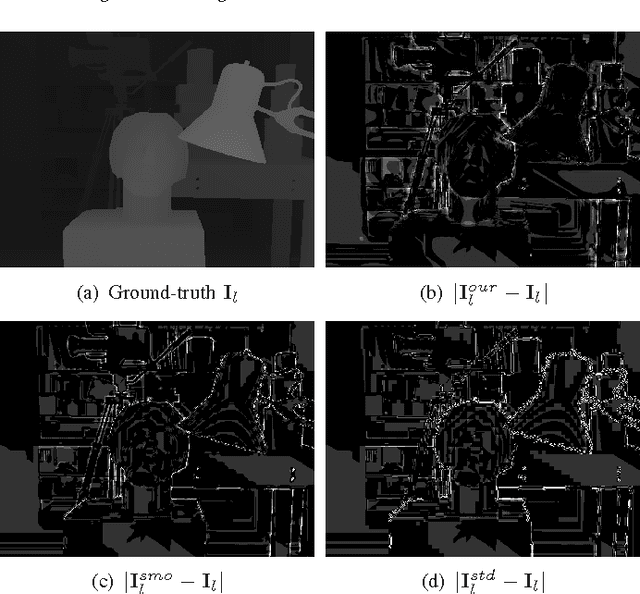
In texture-plus-depth representation of a 3D scene, depth maps from different camera viewpoints are typically lossily compressed via the classical transform coding / coefficient quantization paradigm. In this paper we propose to reduce distortion of the decoded depth maps due to quantization. The key observation is that depth maps from different viewpoints constitute multiple descriptions (MD) of the same 3D scene. Considering the MD jointly, we perform a POCS-like iterative procedure to project a reconstructed signal from one depth map to the other and back, so that the converged depth maps have higher precision than the original quantized versions.

Navigation domain representation for interactive multiview imaging

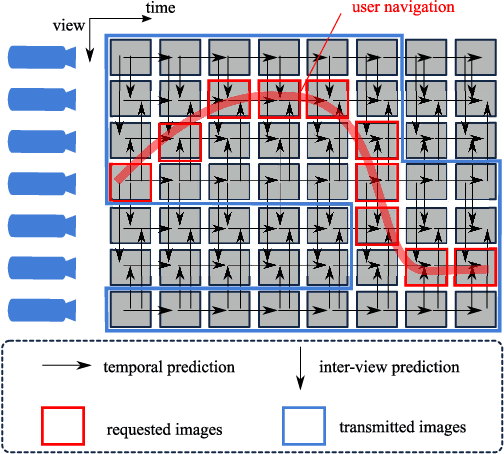
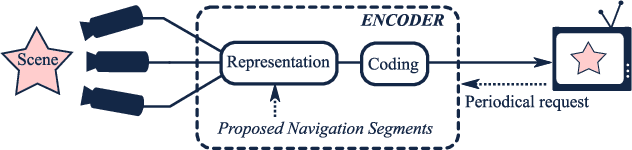
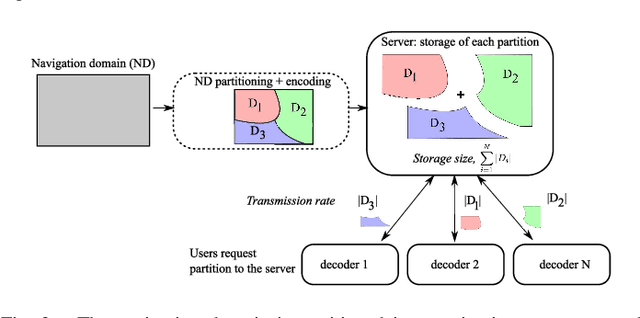
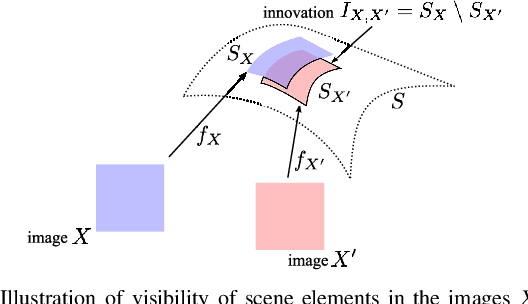
Enabling users to interactively navigate through different viewpoints of a static scene is a new interesting functionality in 3D streaming systems. While it opens exciting perspectives towards rich multimedia applications, it requires the design of novel representations and coding techniques in order to solve the new challenges imposed by interactive navigation. Interactivity clearly brings new design constraints: the encoder is unaware of the exact decoding process, while the decoder has to reconstruct information from incomplete subsets of data since the server can generally not transmit images for all possible viewpoints due to resource constrains. In this paper, we propose a novel multiview data representation that permits to satisfy bandwidth and storage constraints in an interactive multiview streaming system. In particular, we partition the multiview navigation domain into segments, each of which is described by a reference image and some auxiliary information. The auxiliary information enables the client to recreate any viewpoint in the navigation segment via view synthesis. The decoder is then able to navigate freely in the segment without further data request to the server; it requests additional data only when it moves to a different segment. We discuss the benefits of this novel representation in interactive navigation systems and further propose a method to optimize the partitioning of the navigation domain into independent segments, under bandwidth and storage constraints. Experimental results confirm the potential of the proposed representation; namely, our system leads to similar compression performance as classical inter-view coding, while it provides the high level of flexibility that is required for interactive streaming. Hence, our new framework represents a promising solution for 3D data representation in novel interactive multimedia services.