Complex Graph Laplacian Regularizer for Inferencing Grid States

In order to maintain stable grid operations, system monitoring and control processes require the computation of grid states (e.g. voltage magnitude and angles) at high granularity. It is necessary to infer these grid states from measurements generated by a limited number of sensors like phasor measurement units (PMUs) that can be subjected to delays and losses due to channel artefacts, and/or adversarial attacks (e.g. denial of service, jamming, etc.). We propose a novel graph signal processing (GSP) based algorithm to interpolate states of the entire grid from observations of a small number of grid measurements. It is a two-stage process, where first an underlying Hermitian graph is learnt empirically from existing grid datasets. Then, the graph is used to interpolate missing grid signal samples in linear time. With our proposal, we can effectively reconstruct grid signals with significantly smaller number of observations when compared to existing traditional approaches (e.g. state estimation). In contrast to existing GSP approaches, we do not require knowledge of the underlying grid structure and parameters and are able to guarantee fast spectral optimization. We demonstrate the computational efficacy and accuracy of our proposal via practical studies conducted on the IEEE 118 bus system.

Graph Sparsification for GCN Towards Optimal Crop Yield Predictions

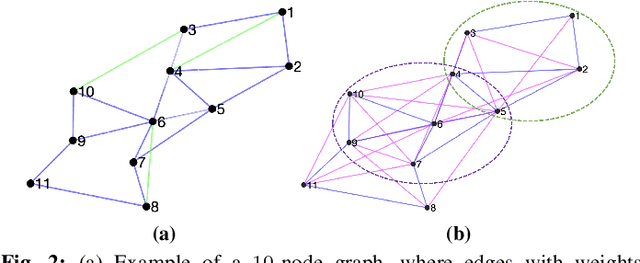
In agronomics, predicting crop yield at a per field/county granularity is important for farmers to minimize uncertainty and plan seeding for the next crop cycle. While state-of-the-art prediction techniques employ graph convolutional nets (GCN) to predict future crop yields given relevant features and crop yields of previous years, a dense underlying graph kernel requires long training and execution time. In this paper, we propose a graph sparsification method based on the Fiedler number to remove edges from a complete graph kernel, in order to lower the complexity of GCN training/execution. Specifically, we first show that greedily removing an edge at a time that induces the minimal change in the second eigenvalue leads to a sparse graph with good GCN performance. We then propose a fast method to choose an edge for removal per iteration based on an eigenvalue perturbation theorem. Experiments show that our Fiedler-based method produces a sparse graph with good GCN performance compared to other graph sparsification schemes in crop yield prediction.

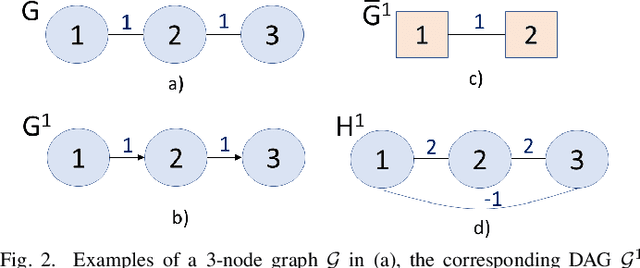
Modeling Viral Information Spreading via Directed Acyclic Graph Diffusion

Viral information like rumors or fake news is spread over a communication network like a virus infection in a unidirectional manner: entity $i$ conveys information to a neighbor $j$, resulting in two equally informed (infected) parties. Existing graph diffusion works focus only on bidirectional diffusion on an undirected graph. Instead, we propose a new directed acyclic graph (DAG) diffusion model to estimate the probability $x_i(t)$ of node $i$'s infection at time $t$ given a source node $s$, where $x_i(\infty)~=~1$. Specifically, given an undirected positive graph modeling node-to-node communication, we first compute its graph embedding: a latent coordinate for each node in an assumed low-dimensional manifold space from extreme eigenvectors via LOBPCG. Next, we construct a DAG based on Euclidean distances between latent coordinates. Spectrally, we prove that the asymmetric DAG Laplacian matrix contains real non-negative eigenvalues, and that the DAG diffusion converges to the all-infection vector $\x(\infty) = \1$ as $t \rightarrow \infty$. Simulation experiments show that our proposed DAG diffusion accurately models viral information spreading over a variety of graph structures at different time instants.

Volumetric Attribute Compression for 3D Point Clouds using Feedforward Network with Geometric Attention

We study 3D point cloud attribute compression using a volumetric approach: given a target volumetric attribute function $f : \mathbb{R}^3 \rightarrow \mathbb{R}$, we quantize and encode parameter vector $\theta$ that characterizes $f$ at the encoder, for reconstruction $f_{\hat{\theta}}(\mathbf{x})$ at known 3D points $\mathbf{x}$'s at the decoder. Extending a previous work Region Adaptive Hierarchical Transform (RAHT) that employs piecewise constant functions to span a nested sequence of function spaces, we propose a feedforward linear network that implements higher-order B-spline bases spanning function spaces without eigen-decomposition. Feedforward network architecture means that the system is amenable to end-to-end neural learning. The key to our network is space-varying convolution, similar to a graph operator, whose weights are computed from the known 3D geometry for normalization. We show that the number of layers in the normalization at the encoder is equivalent to the number of terms in a matrix inverse Taylor series. Experimental results on real-world 3D point clouds show up to 2-3 dB gain over RAHT in energy compaction and 20-30% bitrate reduction.

Efficient Directed Graph Sampling via Gershgorin Disc Alignment

Graph sampling is the problem of choosing a node subset via sampling matrix $\mathbf{H} \in \{0,1\}^{K \times N}$ to collect samples $\mathbf{y} = \mathbf{H} \mathbf{x} \in \mathbb{R}^K$, $K < N$, so that the target signal $\mathbf{x} \in \mathbb{R}^N$ can be reconstructed in high fidelity. While sampling on undirected graphs is well studied, we propose the first sampling scheme tailored specifically for directed graphs, leveraging a previous undirected graph sampling method based on Gershgorin disc alignment (GDAS). Concretely, given a directed positive graph $\mathcal{G}^d$ specified by random-walk graph Laplacian matrix $\mathbf{L}_{rw}$, we first define reconstruction of a smooth signal $\mathbf{x}^*$ from samples $\mathbf{y}$ using graph shift variation (GSV) $\|\mathbf{L}_{rw} \mathbf{x}\|^2_2$ as a signal prior. To minimize worst-case reconstruction error of the linear system solution $\mathbf{x}^* = \mathbf{C}^{-1} \mathbf{H}^\top \mathbf{y}$ with symmetric coefficient matrix $\mathbf{C} = \mathbf{H}^\top \mathbf{H} + \mu \mathbf{L}_{rw}^\top \mathbf{L}_{rw}$, the sampling objective is to choose $\mathbf{H}$ to maximize the smallest eigenvalue $\lambda_{\min}(\mathbf{C})$ of $\mathbf{C}$. To circumvent eigen-decomposition entirely, we maximize instead a lower bound $\lambda^-_{\min}(\mathbf{S}\mathbf{C}\mathbf{S}^{-1})$ of $\lambda_{\min}(\mathbf{C})$ -- smallest Gershgorin disc left-end of a similarity transform of $\mathbf{C}$ -- via a variant of GDAS based on Gershgorin circle theorem (GCT). Experimental results show that our sampling method yields smaller signal reconstruction errors at a faster speed compared to competing schemes.

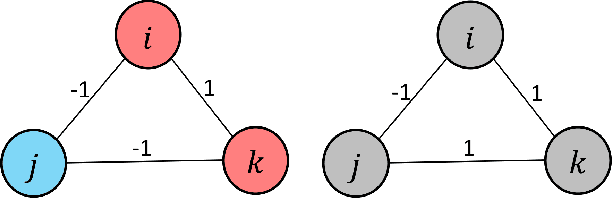
Efficient Signed Graph Sampling via Balancing & Gershgorin Disc Perfect Alignment

A basic premise in graph signal processing (GSP) is that a graph encoding pairwise (anti-)correlations of the targeted signal as edge weights is exploited for graph filtering. However, existing fast graph sampling schemes are designed and tested only for positive graphs describing positive correlations. In this paper, we show that for datasets with strong inherent anti-correlations, a suitable graph contains both positive and negative edge weights. In response, we propose a linear-time signed graph sampling method centered on the concept of balanced signed graphs. Specifically, given an empirical covariance data matrix $\bar{\bf{C}}$, we first learn a sparse inverse matrix (graph Laplacian) $\mathcal{L}$ corresponding to a signed graph $\mathcal{G}$. We define the eigenvectors of Laplacian $\mathcal{L}_B$ for a balanced signed graph $\mathcal{G}_B$ -- approximating $\mathcal{G}$ via edge weight augmentation -- as graph frequency components. Next, we choose samples to minimize the low-pass filter reconstruction error in two steps. We first align all Gershgorin disc left-ends of Laplacian $\mathcal{L}_B$ at smallest eigenvalue $\lambda_{\min}(\mathcal{L}_B)$ via similarity transform $\mathcal{L}_p = \S \mathcal{L}_B \S^{-1}$, leveraging a recent linear algebra theorem called Gershgorin disc perfect alignment (GDPA). We then perform sampling on $\mathcal{L}_p$ using a previous fast Gershgorin disc alignment sampling (GDAS) scheme. Experimental results show that our signed graph sampling method outperformed existing fast sampling schemes noticeably on various datasets.

Unsupervised Graph Spectral Feature Denoising for Crop Yield Prediction

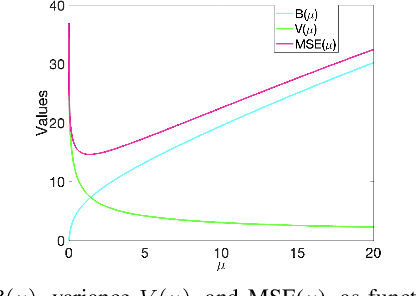
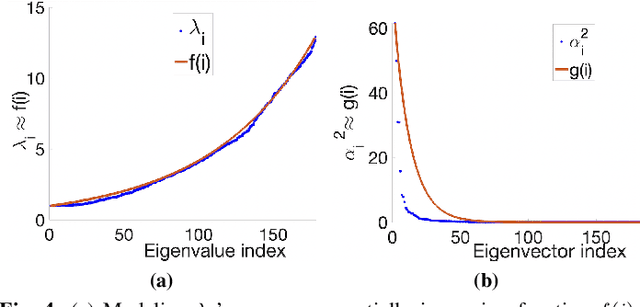
Prediction of annual crop yields at a county granularity is important for national food production and price stability. In this paper, towards the goal of better crop yield prediction, leveraging recent graph signal processing (GSP) tools to exploit spatial correlation among neighboring counties, we denoise relevant features via graph spectral filtering that are inputs to a deep learning prediction model. Specifically, we first construct a combinatorial graph with edge weights that encode county-to-county similarities in soil and location features via metric learning. We then denoise features via a maximum a posteriori (MAP) formulation with a graph Laplacian regularizer (GLR). We focus on the challenge to estimate the crucial weight parameter $\mu$, trading off the fidelity term and GLR, that is a function of noise variance in an unsupervised manner. We first estimate noise variance directly from noise-corrupted graph signals using a graph clique detection (GCD) procedure that discovers locally constant regions. We then compute an optimal $\mu$ minimizing an approximate mean square error function via bias-variance analysis. Experimental results from collected USDA data show that using denoised features as input, performance of a crop yield prediction model can be improved noticeably.

Manifold Graph Signal Restoration using Gradient Graph Laplacian Regularizer

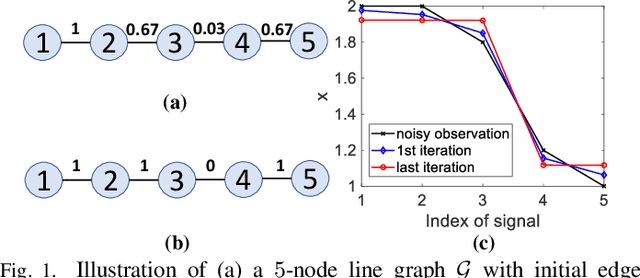
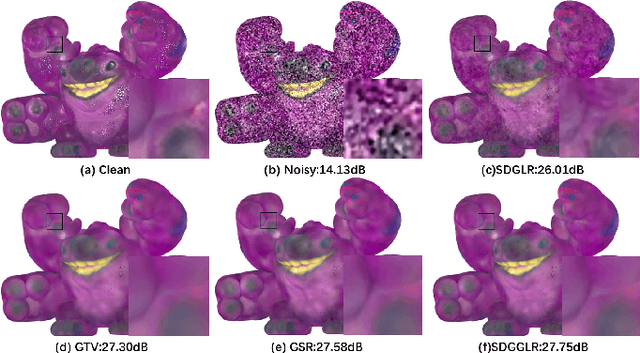
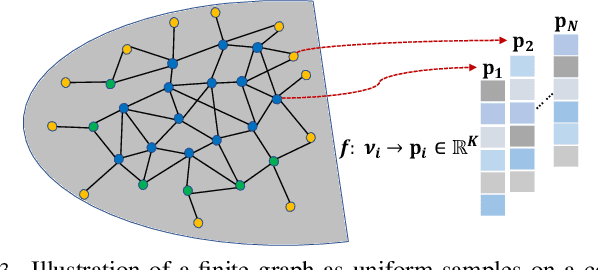
In the graph signal processing (GSP) literature, graph Laplacian regularizer (GLR) was used for signal restoration to promote smooth reconstructions with respect to the underlying graph -- typically signals that are (piecewise) constant. However, for graph signals that are (piecewise) planar, GLR may suffer from the well-known "staircase" effect. In this paper, focusing on manifold graphs -- sets of uniform discrete samples on low-dimensional continuous manifolds -- we generalize GLR to gradient graph Laplacian regularizer (GGLR) that provably promotes piecewise planar (PWP) signal reconstruction. Specifically, for a graph endowed with latent space coordinates (e.g., 2D images, 3D point clouds), we first define a gradient operator, using which we construct a higher-order gradient graph for the computed gradients in each latent dimension. This maps to a gradient-induced nodal graph (GNG) and a Laplacian matrix for a signed graph that is provably positive semi-definite (PSD), thus suitable for quadratic regularization. For manifold graphs without explicit latent coordinates, we propose a fast parameter-free spectral method to first compute latent space coordinates for graph nodes based on generalized eigenvectors. We derive the means-square-error minimizing weight parameter for GGLR efficiently, trading off bias and variance of the signal estimate. Experimental results show that GGLR outperformed previous graph signal priors like GLR and graph total variation (GTV) in a range of graph signal restoration tasks.

Hybrid Model-based / Data-driven Graph Transform for Image Coding

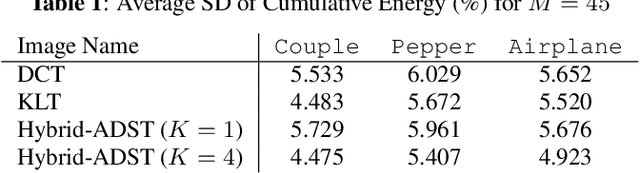
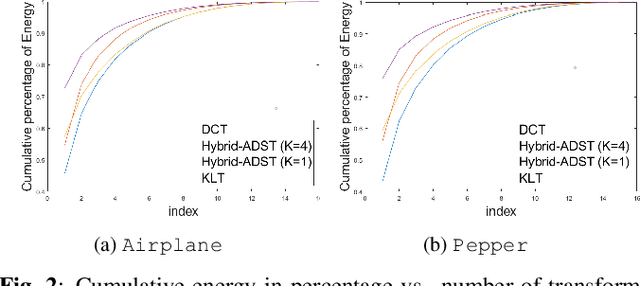
Transform coding to sparsify signal representations remains crucial in an image compression pipeline. While the Karhunen-Lo\`{e}ve transform (KLT) computed from an empirical covariance matrix $\bar{C}$ is theoretically optimal for a stationary process, in practice, collecting sufficient statistics from a non-stationary image to reliably estimate $\bar{C}$ can be difficult. In this paper, to encode an intra-prediction residual block, we pursue a hybrid model-based / data-driven approach: the first $K$ eigenvectors of a transform matrix are derived from a statistical model, e.g., the asymmetric discrete sine transform (ADST), for stability, while the remaining $N-K$ are computed from $\bar{C}$ for performance. The transform computation is posed as a graph learning problem, where we seek a graph Laplacian matrix minimizing a graphical lasso objective inside a convex cone sharing the first $K$ eigenvectors in a Hilbert space of real symmetric matrices. We efficiently solve the problem via augmented Lagrangian relaxation and proximal gradient (PG). Using WebP as a baseline image codec, experimental results show that our hybrid graph transform achieved better energy compaction than default discrete cosine transform (DCT) and better stability than KLT.

Sparse Graph Learning with Eigen-gap for Spectral Filter Training in Graph Convolutional Networks

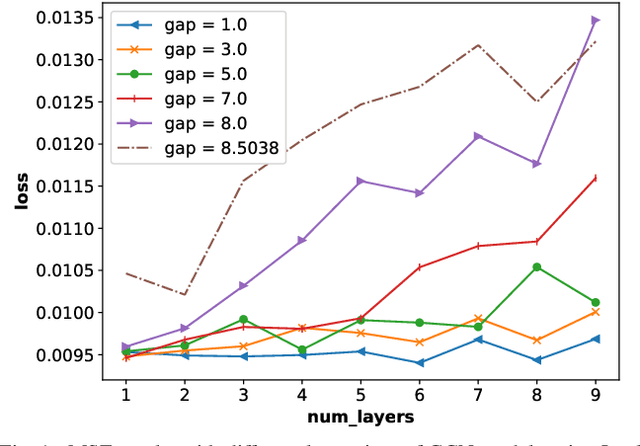
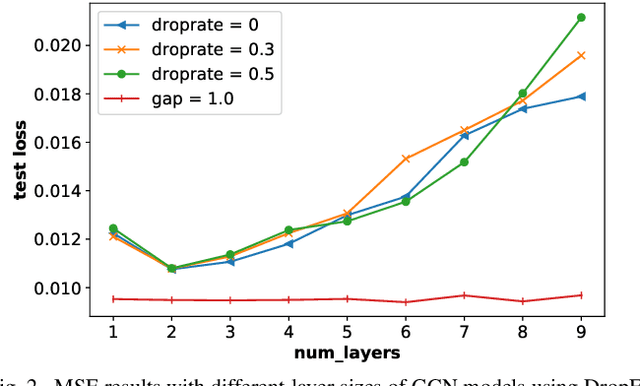
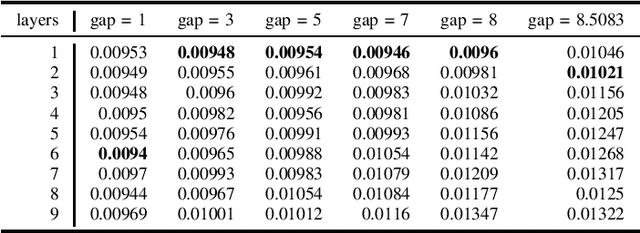
It is now known that the expressive power of graph convolutional neural nets (GCN) does not grow infinitely with the number of layers. Instead, the GCN output approaches a subspace spanned by the first eigenvector of the normalized graph Laplacian matrix with the convergence rate characterized by the "eigen-gap": the difference between the Laplacian's first two distinct eigenvalues. To promote a deeper GCN architecture with sufficient expressiveness, in this paper, given an empirical covariance matrix $\bar{C}$ computed from observable data, we learn a sparse graph Laplacian matrix $L$ closest to $\bar{C}^{-1}$ while maintaining a desirable eigen-gap that slows down convergence. Specifically, we first define a sparse graph learning problem with constraints on the first eigenvector (the most common signal) and the eigen-gap. We solve the corresponding dual problem greedily, where a locally optimal eigen-pair is computed one at a time via a fast approximation of a semi-definite programming (SDP) formulation. The computed $L$ with the desired eigen-gap is normalized spectrally and used for supervised training of GCN for a targeted task. Experiments show that our proposal produced deeper GCNs and smaller errors compared to a competing scheme without explicit eigen-gap optimization.