Opinion Dynamics in Two-Step Process: Message Sources, Opinion Leaders and Normal Agents

According to mass media theory, the dissemination of messages and the evolution of opinions in social networks follow a two-step process. First, opinion leaders receive the message from the message sources, and then they transmit their opinions to normal agents. However, most opinion models only consider the evolution of opinions within a single network, which fails to capture the two-step process accurately. To address this limitation, we propose a unified framework called the Two-Step Model, which analyzes the communication process among message sources, opinion leaders, and normal agents. In this study, we examine the steady-state opinions and stability of the Two-Step Model. Our findings reveal that several factors, such as message distribution, initial opinion, level of stubbornness, and preference coefficient, influence the sample mean and variance of steady-state opinions. Notably, normal agents' opinions tend to be influenced by opinion leaders in the two-step process. We also conduct numerical and social experiments to validate the accuracy of the Two-Step Model, which outperforms other models on average. Our results provide valuable insights into the factors that shape social opinions and can guide the development of effective strategies for opinion guidance in social networks.

Modeling Viral Information Spreading via Directed Acyclic Graph Diffusion

Viral information like rumors or fake news is spread over a communication network like a virus infection in a unidirectional manner: entity $i$ conveys information to a neighbor $j$, resulting in two equally informed (infected) parties. Existing graph diffusion works focus only on bidirectional diffusion on an undirected graph. Instead, we propose a new directed acyclic graph (DAG) diffusion model to estimate the probability $x_i(t)$ of node $i$'s infection at time $t$ given a source node $s$, where $x_i(\infty)~=~1$. Specifically, given an undirected positive graph modeling node-to-node communication, we first compute its graph embedding: a latent coordinate for each node in an assumed low-dimensional manifold space from extreme eigenvectors via LOBPCG. Next, we construct a DAG based on Euclidean distances between latent coordinates. Spectrally, we prove that the asymmetric DAG Laplacian matrix contains real non-negative eigenvalues, and that the DAG diffusion converges to the all-infection vector $\x(\infty) = \1$ as $t \rightarrow \infty$. Simulation experiments show that our proposed DAG diffusion accurately models viral information spreading over a variety of graph structures at different time instants.

Efficient Directed Graph Sampling via Gershgorin Disc Alignment

Graph sampling is the problem of choosing a node subset via sampling matrix $\mathbf{H} \in \{0,1\}^{K \times N}$ to collect samples $\mathbf{y} = \mathbf{H} \mathbf{x} \in \mathbb{R}^K$, $K < N$, so that the target signal $\mathbf{x} \in \mathbb{R}^N$ can be reconstructed in high fidelity. While sampling on undirected graphs is well studied, we propose the first sampling scheme tailored specifically for directed graphs, leveraging a previous undirected graph sampling method based on Gershgorin disc alignment (GDAS). Concretely, given a directed positive graph $\mathcal{G}^d$ specified by random-walk graph Laplacian matrix $\mathbf{L}_{rw}$, we first define reconstruction of a smooth signal $\mathbf{x}^*$ from samples $\mathbf{y}$ using graph shift variation (GSV) $\|\mathbf{L}_{rw} \mathbf{x}\|^2_2$ as a signal prior. To minimize worst-case reconstruction error of the linear system solution $\mathbf{x}^* = \mathbf{C}^{-1} \mathbf{H}^\top \mathbf{y}$ with symmetric coefficient matrix $\mathbf{C} = \mathbf{H}^\top \mathbf{H} + \mu \mathbf{L}_{rw}^\top \mathbf{L}_{rw}$, the sampling objective is to choose $\mathbf{H}$ to maximize the smallest eigenvalue $\lambda_{\min}(\mathbf{C})$ of $\mathbf{C}$. To circumvent eigen-decomposition entirely, we maximize instead a lower bound $\lambda^-_{\min}(\mathbf{S}\mathbf{C}\mathbf{S}^{-1})$ of $\lambda_{\min}(\mathbf{C})$ -- smallest Gershgorin disc left-end of a similarity transform of $\mathbf{C}$ -- via a variant of GDAS based on Gershgorin circle theorem (GCT). Experimental results show that our sampling method yields smaller signal reconstruction errors at a faster speed compared to competing schemes.

Rethinking Position Bias Modeling with Knowledge Distillation for CTR Prediction

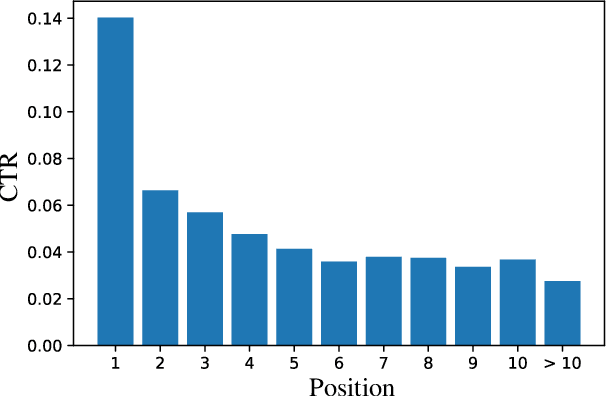
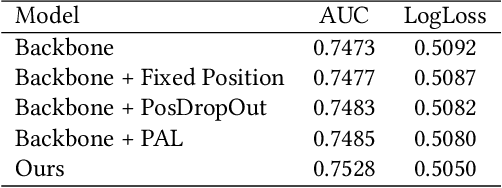
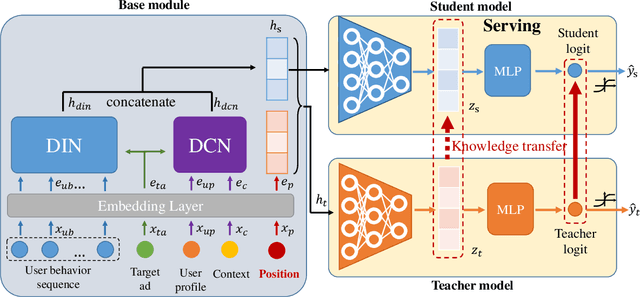
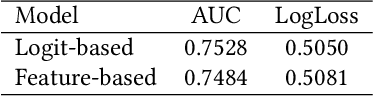
Click-through rate (CTR) Prediction is of great importance in real-world online ads systems. One challenge for the CTR prediction task is to capture the real interest of users from their clicked items, which is inherently biased by presented positions of items, i.e., more front positions tend to obtain higher CTR values. A popular line of existing works focuses on explicitly estimating position bias by result randomization which is expensive and inefficient, or by inverse propensity weighting (IPW) which relies heavily on the quality of the propensity estimation. Another common solution is modeling position as features during offline training and simply adopting fixed value or dropout tricks when serving. However, training-inference inconsistency can lead to sub-optimal performance. Furthermore, post-click information such as position values is informative while less exploited in CTR prediction. This work proposes a simple yet efficient knowledge distillation framework to alleviate the impact of position bias and leverage position information to improve CTR prediction. We demonstrate the performance of our proposed method on a real-world production dataset and online A/B tests, achieving significant improvements over competing baseline models. The proposed method has been deployed in the real world online ads systems, serving main traffic on one of the world's largest e-commercial platforms.

Concept Drift Adaptation for CTR Prediction in Online Advertising Systems

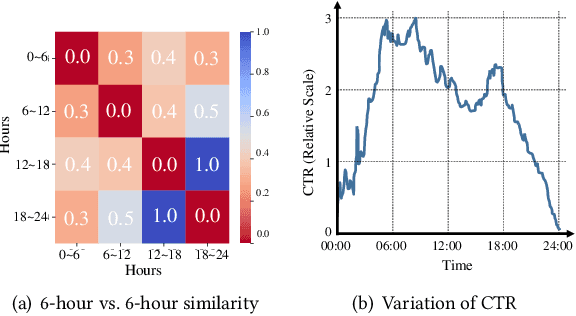
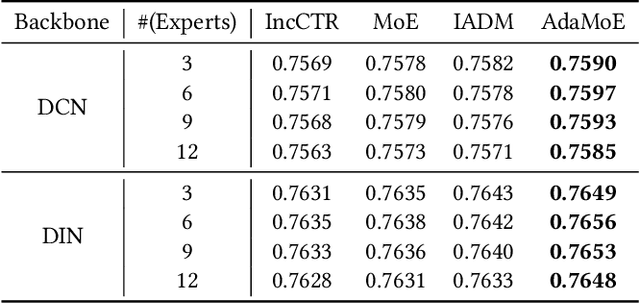
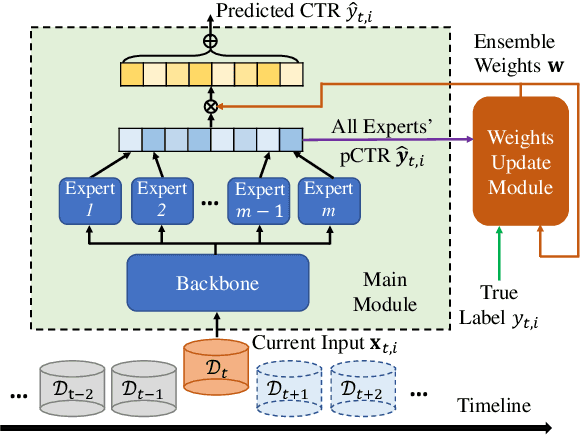
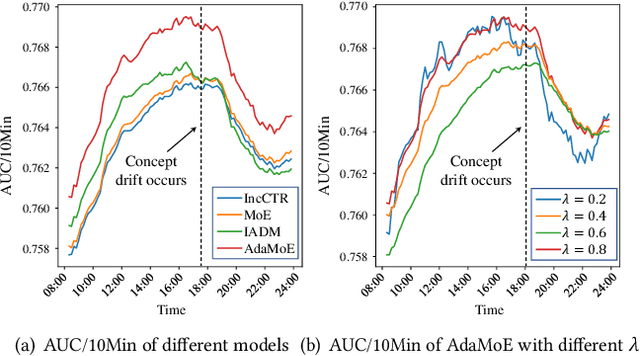
Click-through rate (CTR) prediction is a crucial task in web search, recommender systems, and online advertisement displaying. In practical application, CTR models often serve with high-speed user-generated data streams, whose underlying distribution rapidly changing over time. The concept drift problem inevitably exists in those streaming data, which can lead to performance degradation due to the timeliness issue. To ensure model freshness, incremental learning has been widely adopted in real-world production systems. However, it is hard for the incremental update to achieve the balance of the CTR models between the adaptability to capture the fast-changing trends and generalization ability to retain common knowledge. In this paper, we propose adaptive mixture of experts (AdaMoE), a new framework to alleviate the concept drift problem by adaptive filtering in the data stream of CTR prediction. The extensive experiments on the offline industrial dataset and online A/B tests show that our AdaMoE significantly outperforms all incremental learning frameworks considered.

Table2Charts: Learning Shared Representations for Recommending Charts on Multi-dimensional Data

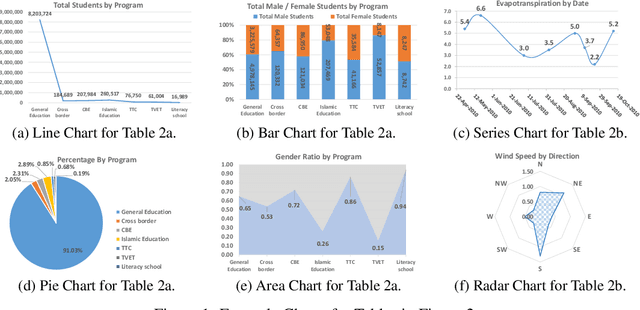
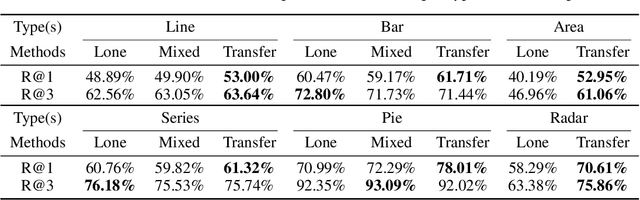
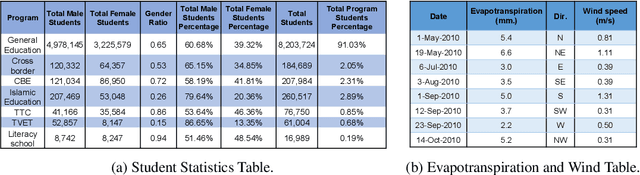
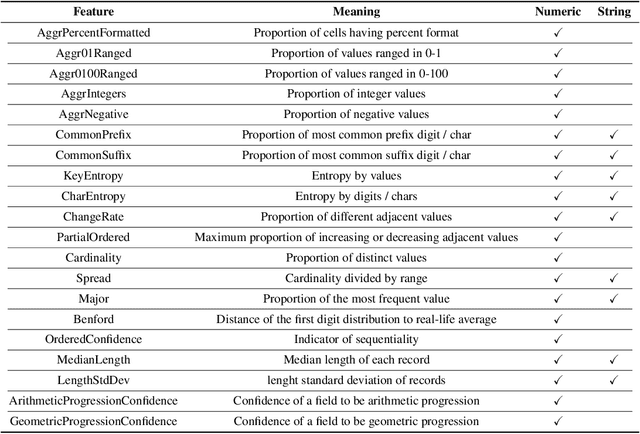
It is common for people to create different types of charts to explore a multi-dimensional dataset (table). However, to build an intelligent assistant that recommends commonly composed charts, the fundamental problems of "multi-dialect" unification, imbalanced data and open vocabulary exist. In this paper, we propose Table2Charts framework which learns common patterns from a large corpus of (table, charts) pairs. Based on deep Q-learning with copying mechanism and heuristic searching, Table2Charts does table-to-sequence generation, where each sequence follows a chart template. On a large spreadsheet corpus with 196k tables and 306k charts, we show that Table2Charts could learn a shared representation of table fields so that tasks on different chart types could mutually enhance each other. Table2Charts has >0.61 recall at top-3 and >0.49 recall at top-1 for both single-type and multi-type chart recommendation tasks.