Efficient Signed Graph Sampling via Balancing & Gershgorin Disc Perfect Alignment
Paper and Code
Aug 18, 2022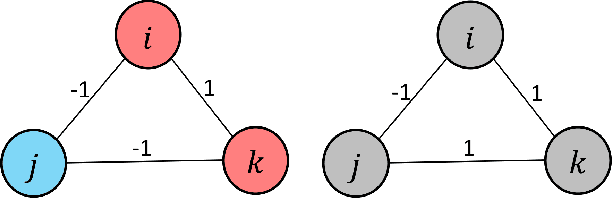
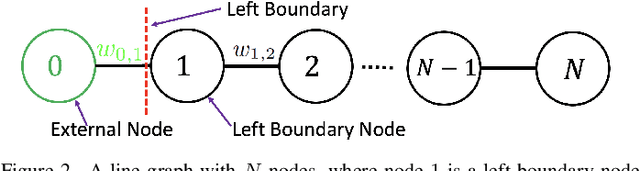
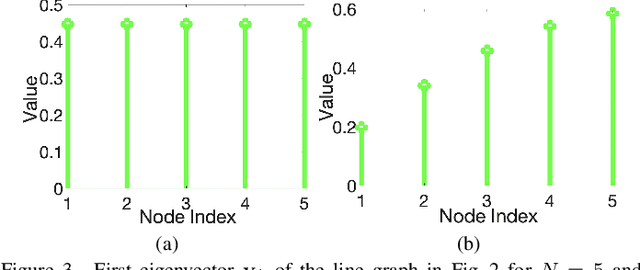
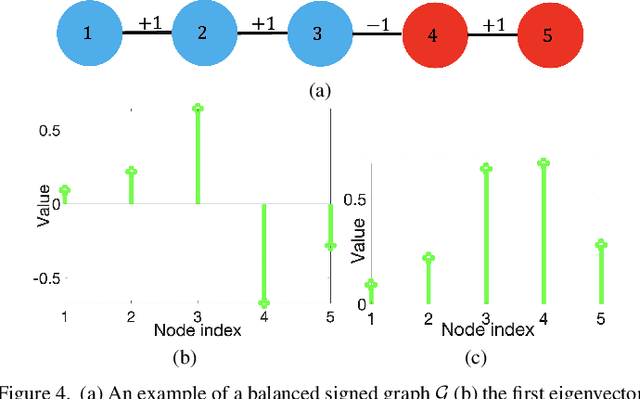
A basic premise in graph signal processing (GSP) is that a graph encoding pairwise (anti-)correlations of the targeted signal as edge weights is exploited for graph filtering. However, existing fast graph sampling schemes are designed and tested only for positive graphs describing positive correlations. In this paper, we show that for datasets with strong inherent anti-correlations, a suitable graph contains both positive and negative edge weights. In response, we propose a linear-time signed graph sampling method centered on the concept of balanced signed graphs. Specifically, given an empirical covariance data matrix $\bar{\bf{C}}$, we first learn a sparse inverse matrix (graph Laplacian) $\mathcal{L}$ corresponding to a signed graph $\mathcal{G}$. We define the eigenvectors of Laplacian $\mathcal{L}_B$ for a balanced signed graph $\mathcal{G}_B$ -- approximating $\mathcal{G}$ via edge weight augmentation -- as graph frequency components. Next, we choose samples to minimize the low-pass filter reconstruction error in two steps. We first align all Gershgorin disc left-ends of Laplacian $\mathcal{L}_B$ at smallest eigenvalue $\lambda_{\min}(\mathcal{L}_B)$ via similarity transform $\mathcal{L}_p = \S \mathcal{L}_B \S^{-1}$, leveraging a recent linear algebra theorem called Gershgorin disc perfect alignment (GDPA). We then perform sampling on $\mathcal{L}_p$ using a previous fast Gershgorin disc alignment sampling (GDAS) scheme. Experimental results show that our signed graph sampling method outperformed existing fast sampling schemes noticeably on various datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge