Hybrid Model-based / Data-driven Graph Transform for Image Coding
Paper and Code
Mar 02, 2022
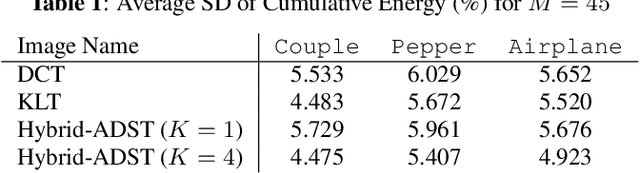
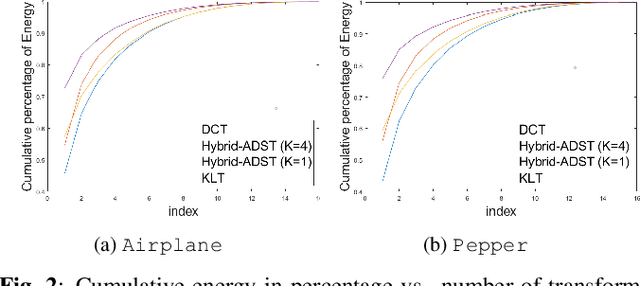

Transform coding to sparsify signal representations remains crucial in an image compression pipeline. While the Karhunen-Lo\`{e}ve transform (KLT) computed from an empirical covariance matrix $\bar{C}$ is theoretically optimal for a stationary process, in practice, collecting sufficient statistics from a non-stationary image to reliably estimate $\bar{C}$ can be difficult. In this paper, to encode an intra-prediction residual block, we pursue a hybrid model-based / data-driven approach: the first $K$ eigenvectors of a transform matrix are derived from a statistical model, e.g., the asymmetric discrete sine transform (ADST), for stability, while the remaining $N-K$ are computed from $\bar{C}$ for performance. The transform computation is posed as a graph learning problem, where we seek a graph Laplacian matrix minimizing a graphical lasso objective inside a convex cone sharing the first $K$ eigenvectors in a Hilbert space of real symmetric matrices. We efficiently solve the problem via augmented Lagrangian relaxation and proximal gradient (PG). Using WebP as a baseline image codec, experimental results show that our hybrid graph transform achieved better energy compaction than default discrete cosine transform (DCT) and better stability than KLT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge