Bayesian Binary Search

We present Bayesian Binary Search (BBS), a novel probabilistic variant of the classical binary search/bisection algorithm. BBS leverages machine learning/statistical techniques to estimate the probability density of the search space and modifies the bisection step to split based on probability density rather than the traditional midpoint, allowing for the learned distribution of the search space to guide the search algorithm. Search space density estimation can flexibly be performed using supervised probabilistic machine learning techniques (e.g., Gaussian process regression, Bayesian neural networks, quantile regression) or unsupervised learning algorithms (e.g., Gaussian mixture models, kernel density estimation (KDE), maximum likelihood estimation (MLE)). We demonstrate significant efficiency gains of using BBS on both simulated data across a variety of distributions and in a real-world binary search use case of probing channel balances in the Bitcoin Lightning Network, for which we have deployed the BBS algorithm in a production setting.

Do We Really Need to Drop Items with Missing Modalities in Multimodal Recommendation?

Generally, items with missing modalities are dropped in multimodal recommendation. However, with this work, we question this procedure, highlighting that it would further damage the pipeline of any multimodal recommender system. First, we show that the lack of (some) modalities is, in fact, a widely-diffused phenomenon in multimodal recommendation. Second, we propose a pipeline that imputes missing multimodal features in recommendation by leveraging traditional imputation strategies in machine learning. Then, given the graph structure of the recommendation data, we also propose three more effective imputation solutions that leverage the item-item co-purchase graph and the multimodal similarities of co-interacted items. Our method can be plugged into any multimodal RSs in the literature working as an untrained pre-processing phase, showing (through extensive experiments) that any data pre-filtering is not only unnecessary but also harmful to the performance.

UTG: Towards a Unified View of Snapshot and Event Based Models for Temporal Graphs

Temporal graphs have gained increasing importance due to their ability to model dynamically evolving relationships. These graphs can be represented through either a stream of edge events or a sequence of graph snapshots. Until now, the development of machine learning methods for both types has occurred largely in isolation, resulting in limited experimental comparison and theoretical crosspollination between the two. In this paper, we introduce Unified Temporal Graph (UTG), a framework that unifies snapshot-based and event-based machine learning models under a single umbrella, enabling models developed for one representation to be applied effectively to datasets of the other. We also propose a novel UTG training procedure to boost the performance of snapshot-based models in the streaming setting. We comprehensively evaluate both snapshot and event-based models across both types of temporal graphs on the temporal link prediction task. Our main findings are threefold: first, when combined with UTG training, snapshotbased models can perform competitively with event-based models such as TGN and GraphMixer even on event datasets. Second, snapshot-based models are at least an order of magnitude faster than most event-based models during inference. Third, while event-based methods such as NAT and DyGFormer outperforms snapshotbased methods on both types of temporal graphs, this is because they leverage joint neighborhood structural features thus emphasizing the potential to incorporate these features into snapshot-based models as well. These findings highlight the importance of comparing model architectures independent of the data format and suggest the potential of combining the efficiency of snapshot-based models with the performance of event-based models in the future.

TGB 2.0: A Benchmark for Learning on Temporal Knowledge Graphs and Heterogeneous Graphs

Multi-relational temporal graphs are powerful tools for modeling real-world data, capturing the evolving and interconnected nature of entities over time. Recently, many novel models are proposed for ML on such graphs intensifying the need for robust evaluation and standardized benchmark datasets. However, the availability of such resources remains scarce and evaluation faces added complexity due to reproducibility issues in experimental protocols. To address these challenges, we introduce Temporal Graph Benchmark 2.0 (TGB 2.0), a novel benchmarking framework tailored for evaluating methods for predicting future links on Temporal Knowledge Graphs and Temporal Heterogeneous Graphs with a focus on large-scale datasets, extending the Temporal Graph Benchmark. TGB 2.0 facilitates comprehensive evaluations by presenting eight novel datasets spanning five domains with up to 53 million edges. TGB 2.0 datasets are significantly larger than existing datasets in terms of number of nodes, edges, or timestamps. In addition, TGB 2.0 provides a reproducible and realistic evaluation pipeline for multi-relational temporal graphs. Through extensive experimentation, we observe that 1) leveraging edge-type information is crucial to obtain high performance, 2) simple heuristic baselines are often competitive with more complex methods, 3) most methods fail to run on our largest datasets, highlighting the need for research on more scalable methods.

Channel Balance Interpolation in the Lightning Network via Machine Learning

The Bitcoin Lightning Network is a Layer 2 payment protocol that addresses Bitcoin's scalability by facilitating quick and cost effective transactions through payment channels. This research explores the feasibility of using machine learning models to interpolate channel balances within the network, which can be used for optimizing the network's pathfinding algorithms. While there has been much exploration in balance probing and multipath payment protocols, predicting channel balances using solely node and channel features remains an uncharted area. This paper evaluates the performance of several machine learning models against two heuristic baselines and investigates the predictive capabilities of various features. Our model performs favorably in experimental evaluation, outperforming by 10% against an equal split baseline where both edges are assigned half of the channel capacity.

Dealing with Missing Modalities in Multimodal Recommendation: a Feature Propagation-based Approach

Multimodal recommender systems work by augmenting the representation of the products in the catalogue through multimodal features extracted from images, textual descriptions, or audio tracks characterising such products. Nevertheless, in real-world applications, only a limited percentage of products come with multimodal content to extract meaningful features from, making it hard to provide accurate recommendations. To the best of our knowledge, very few attention has been put into the problem of missing modalities in multimodal recommendation so far. To this end, our paper comes as a preliminary attempt to formalise and address such an issue. Inspired by the recent advances in graph representation learning, we propose to re-sketch the missing modalities problem as a problem of missing graph node features to apply the state-of-the-art feature propagation algorithm eventually. Technically, we first project the user-item graph into an item-item one based on co-interactions. Then, leveraging the multimodal similarities among co-interacted items, we apply a modified version of the feature propagation technique to impute the missing multimodal features. Adopted as a pre-processing stage for two recent multimodal recommender systems, our simple approach performs better than other shallower solutions on three popular datasets.

Temporal Graph Benchmark for Machine Learning on Temporal Graphs

We present the Temporal Graph Benchmark (TGB), a collection of challenging and diverse benchmark datasets for realistic, reproducible, and robust evaluation of machine learning models on temporal graphs. TGB datasets are of large scale, spanning years in duration, incorporate both node and edge-level prediction tasks and cover a diverse set of domains including social, trade, transaction, and transportation networks. For both tasks, we design evaluation protocols based on realistic use-cases. We extensively benchmark each dataset and find that the performance of common models can vary drastically across datasets. In addition, on dynamic node property prediction tasks, we show that simple methods often achieve superior performance compared to existing temporal graph models. We believe that these findings open up opportunities for future research on temporal graphs. Finally, TGB provides an automated machine learning pipeline for reproducible and accessible temporal graph research, including data loading, experiment setup and performance evaluation. TGB will be maintained and updated on a regular basis and welcomes community feedback. TGB datasets, data loaders, example codes, evaluation setup, and leaderboards are publicly available at https://tgb.complexdatalab.com/ .

Edge Directionality Improves Learning on Heterophilic Graphs

Graph Neural Networks (GNNs) have become the de-facto standard tool for modeling relational data. However, while many real-world graphs are directed, the majority of today's GNN models discard this information altogether by simply making the graph undirected. The reasons for this are historical: 1) many early variants of spectral GNNs explicitly required undirected graphs, and 2) the first benchmarks on homophilic graphs did not find significant gain from using direction. In this paper, we show that in heterophilic settings, treating the graph as directed increases the effective homophily of the graph, suggesting a potential gain from the correct use of directionality information. To this end, we introduce Directed Graph Neural Network (Dir-GNN), a novel general framework for deep learning on directed graphs. Dir-GNN can be used to extend any Message Passing Neural Network (MPNN) to account for edge directionality information by performing separate aggregations of the incoming and outgoing edges. We prove that Dir-GNN matches the expressivity of the Directed Weisfeiler-Lehman test, exceeding that of conventional MPNNs. In extensive experiments, we validate that while our framework leaves performance unchanged on homophilic datasets, it leads to large gains over base models such as GCN, GAT and GraphSage on heterophilic benchmarks, outperforming much more complex methods and achieving new state-of-the-art results.

Graph Neural Networks for Link Prediction with Subgraph Sketching

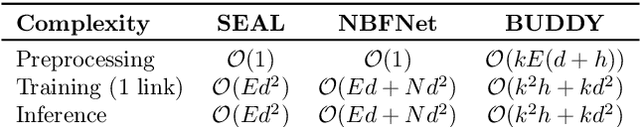
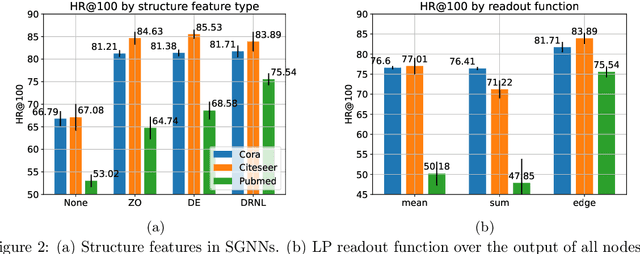
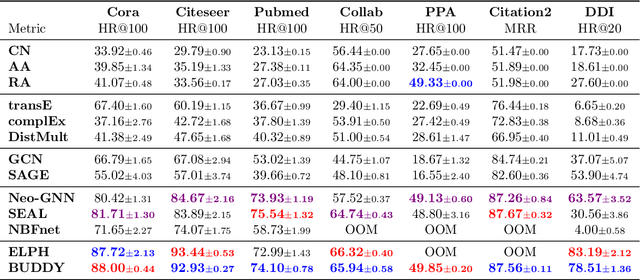
Many Graph Neural Networks (GNNs) perform poorly compared to simple heuristics on Link Prediction (LP) tasks. This is due to limitations in expressive power such as the inability to count triangles (the backbone of most LP heuristics) and because they can not distinguish automorphic nodes (those having identical structural roles). Both expressiveness issues can be alleviated by learning link (rather than node) representations and incorporating structural features such as triangle counts. Since explicit link representations are often prohibitively expensive, recent works resorted to subgraph-based methods, which have achieved state-of-the-art performance for LP, but suffer from poor efficiency due to high levels of redundancy between subgraphs. We analyze the components of subgraph GNN (SGNN) methods for link prediction. Based on our analysis, we propose a novel full-graph GNN called ELPH (Efficient Link Prediction with Hashing) that passes subgraph sketches as messages to approximate the key components of SGNNs without explicit subgraph construction. ELPH is provably more expressive than Message Passing GNNs (MPNNs). It outperforms existing SGNN models on many standard LP benchmarks while being orders of magnitude faster. However, it shares the common GNN limitation that it is only efficient when the dataset fits in GPU memory. Accordingly, we develop a highly scalable model, called BUDDY, which uses feature precomputation to circumvent this limitation without sacrificing predictive performance. Our experiments show that BUDDY also outperforms SGNNs on standard LP benchmarks while being highly scalable and faster than ELPH.

Learning to Infer Structures of Network Games

Strategic interactions between a group of individuals or organisations can be modelled as games played on networks, where a player's payoff depends not only on their actions but also on those of their neighbours. Inferring the network structure from observed game outcomes (equilibrium actions) is an important problem with numerous potential applications in economics and social sciences. Existing methods mostly require the knowledge of the utility function associated with the game, which is often unrealistic to obtain in real-world scenarios. We adopt a transformer-like architecture which correctly accounts for the symmetries of the problem and learns a mapping from the equilibrium actions to the network structure of the game without explicit knowledge of the utility function. We test our method on three different types of network games using both synthetic and real-world data, and demonstrate its effectiveness in network structure inference and superior performance over existing methods.