SymmCD: Symmetry-Preserving Crystal Generation with Diffusion Models

Generating novel crystalline materials has potential to lead to advancements in fields such as electronics, energy storage, and catalysis. The defining characteristic of crystals is their symmetry, which plays a central role in determining their physical properties. However, existing crystal generation methods either fail to generate materials that display the symmetries of real-world crystals, or simply replicate the symmetry information from examples in a database. To address this limitation, we propose SymmCD, a novel diffusion-based generative model that explicitly incorporates crystallographic symmetry into the generative process. We decompose crystals into two components and learn their joint distribution through diffusion: 1) the asymmetric unit, the smallest subset of the crystal which can generate the whole crystal through symmetry transformations, and; 2) the symmetry transformations needed to be applied to each atom in the asymmetric unit. We also use a novel and interpretable representation for these transformations, enabling generalization across different crystallographic symmetry groups. We showcase the competitive performance of SymmCD on a subset of the Materials Project, obtaining diverse and valid crystals with realistic symmetries and predicted properties.

Symmetry-Aware Generative Modeling through Learned Canonicalization

Generative modeling of symmetric densities has a range of applications in AI for science, from drug discovery to physics simulations. The existing generative modeling paradigm for invariant densities combines an invariant prior with an equivariant generative process. However, we observe that this technique is not necessary and has several drawbacks resulting from the limitations of equivariant networks. Instead, we propose to model a learned slice of the density so that only one representative element per orbit is learned. To accomplish this, we learn a group-equivariant canonicalization network that maps training samples to a canonical pose and train a non-equivariant generative model over these canonicalized samples. We implement this idea in the context of diffusion models. Our preliminary experimental results on molecular modeling are promising, demonstrating improved sample quality and faster inference time.

OpenAI o1 System Card

The o1 model series is trained with large-scale reinforcement learning to reason using chain of thought. These advanced reasoning capabilities provide new avenues for improving the safety and robustness of our models. In particular, our models can reason about our safety policies in context when responding to potentially unsafe prompts, through deliberative alignment. This leads to state-of-the-art performance on certain benchmarks for risks such as generating illicit advice, choosing stereotyped responses, and succumbing to known jailbreaks. Training models to incorporate a chain of thought before answering has the potential to unlock substantial benefits, while also increasing potential risks that stem from heightened intelligence. Our results underscore the need for building robust alignment methods, extensively stress-testing their efficacy, and maintaining meticulous risk management protocols. This report outlines the safety work carried out for the OpenAI o1 and OpenAI o1-mini models, including safety evaluations, external red teaming, and Preparedness Framework evaluations.

GPT-4o System Card

GPT-4o is an autoregressive omni model that accepts as input any combination of text, audio, image, and video, and generates any combination of text, audio, and image outputs. It's trained end-to-end across text, vision, and audio, meaning all inputs and outputs are processed by the same neural network. GPT-4o can respond to audio inputs in as little as 232 milliseconds, with an average of 320 milliseconds, which is similar to human response time in conversation. It matches GPT-4 Turbo performance on text in English and code, with significant improvement on text in non-English languages, while also being much faster and 50\% cheaper in the API. GPT-4o is especially better at vision and audio understanding compared to existing models. In line with our commitment to building AI safely and consistent with our voluntary commitments to the White House, we are sharing the GPT-4o System Card, which includes our Preparedness Framework evaluations. In this System Card, we provide a detailed look at GPT-4o's capabilities, limitations, and safety evaluations across multiple categories, focusing on speech-to-speech while also evaluating text and image capabilities, and measures we've implemented to ensure the model is safe and aligned. We also include third-party assessments on dangerous capabilities, as well as discussion of potential societal impacts of GPT-4o's text and vision capabilities.

E(3)-Equivariant Mesh Neural Networks

Triangular meshes are widely used to represent three-dimensional objects. As a result, many recent works have address the need for geometric deep learning on 3D mesh. However, we observe that the complexities in many of these architectures does not translate to practical performance, and simple deep models for geometric graphs are competitive in practice. Motivated by this observation, we minimally extend the update equations of E(n)-Equivariant Graph Neural Networks (EGNNs) (Satorras et al., 2021) to incorporate mesh face information, and further improve it to account for long-range interactions through hierarchy. The resulting architecture, Equivariant Mesh Neural Network (EMNN), outperforms other, more complicated equivariant methods on mesh tasks, with a fast run-time and no expensive pre-processing. Our implementation is available at https://github.com/HySonLab/EquiMesh

Using Multiple Vector Channels Improves E(n)-Equivariant Graph Neural Networks

We present a natural extension to E(n)-equivariant graph neural networks that uses multiple equivariant vectors per node. We formulate the extension and show that it improves performance across different physical systems benchmark tasks, with minimal differences in runtime or number of parameters. The proposed multichannel EGNN outperforms the standard singlechannel EGNN on N-body charged particle dynamics, molecular property predictions, and predicting the trajectories of solar system bodies. Given the additional benefits and minimal additional cost of multi-channel EGNN, we suggest that this extension may be of practical use to researchers working in machine learning for the physical sciences

Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.

Distributionally Robust Multilingual Machine Translation

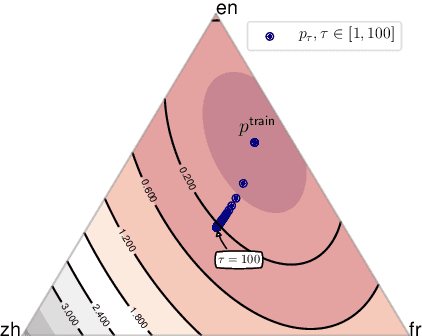
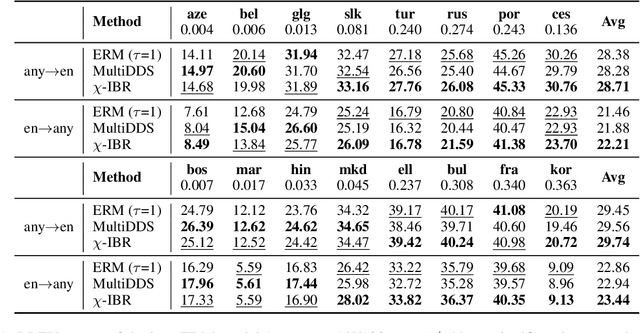
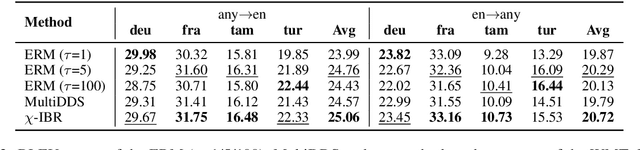
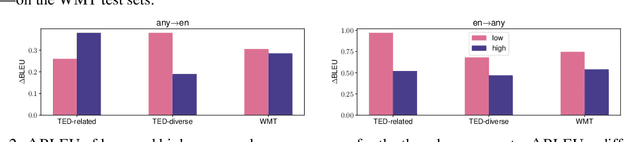
Multilingual neural machine translation (MNMT) learns to translate multiple language pairs with a single model, potentially improving both the accuracy and the memory-efficiency of deployed models. However, the heavy data imbalance between languages hinders the model from performing uniformly across language pairs. In this paper, we propose a new learning objective for MNMT based on distributionally robust optimization, which minimizes the worst-case expected loss over the set of language pairs. We further show how to practically optimize this objective for large translation corpora using an iterated best response scheme, which is both effective and incurs negligible additional computational cost compared to standard empirical risk minimization. We perform extensive experiments on three sets of languages from two datasets and show that our method consistently outperforms strong baseline methods in terms of average and per-language performance under both many-to-one and one-to-many translation settings.

Adapting to Function Difficulty and Growth Conditions in Private Optimization

We develop algorithms for private stochastic convex optimization that adapt to the hardness of the specific function we wish to optimize. While previous work provide worst-case bounds for arbitrary convex functions, it is often the case that the function at hand belongs to a smaller class that enjoys faster rates. Concretely, we show that for functions exhibiting $\kappa$-growth around the optimum, i.e., $f(x) \ge f(x^*) + \lambda \kappa^{-1} \|x-x^*\|_2^\kappa$ for $\kappa > 1$, our algorithms improve upon the standard ${\sqrt{d}}/{n\varepsilon}$ privacy rate to the faster $({\sqrt{d}}/{n\varepsilon})^{\tfrac{\kappa}{\kappa - 1}}$. Crucially, they achieve these rates without knowledge of the growth constant $\kappa$ of the function. Our algorithms build upon the inverse sensitivity mechanism, which adapts to instance difficulty (Asi & Duchi, 2020), and recent localization techniques in private optimization (Feldman et al., 2020). We complement our algorithms with matching lower bounds for these function classes and demonstrate that our adaptive algorithm is \emph{simultaneously} (minimax) optimal over all $\kappa \ge 1+c$ whenever $c = \Theta(1)$.

Learning with User-Level Privacy

We propose and analyze algorithms to solve a range of learning tasks under user-level differential privacy constraints. Rather than guaranteeing only the privacy of individual samples, user-level DP protects a user's entire contribution ($m \ge 1$ samples), providing more stringent but more realistic protection against information leaks. We show that for high-dimensional mean estimation, empirical risk minimization with smooth losses, stochastic convex optimization, and learning hypothesis class with finite metric entropy, the privacy cost decreases as $O(1/\sqrt{m})$ as users provide more samples. In contrast, when increasing the number of users $n$, the privacy cost decreases at a faster $O(1/n)$ rate. We complement these results with lower bounds showing the worst-case optimality of our algorithm for mean estimation and stochastic convex optimization. Our algorithms rely on novel techniques for private mean estimation in arbitrary dimension with error scaling as the concentration radius $\tau$ of the distribution rather than the entire range. Under uniform convergence, we derive an algorithm that privately answers a sequence of $K$ adaptively chosen queries with privacy cost proportional to $\tau$, and apply it to solve the learning tasks we consider.