Mean estimation in the add-remove model of differential privacy

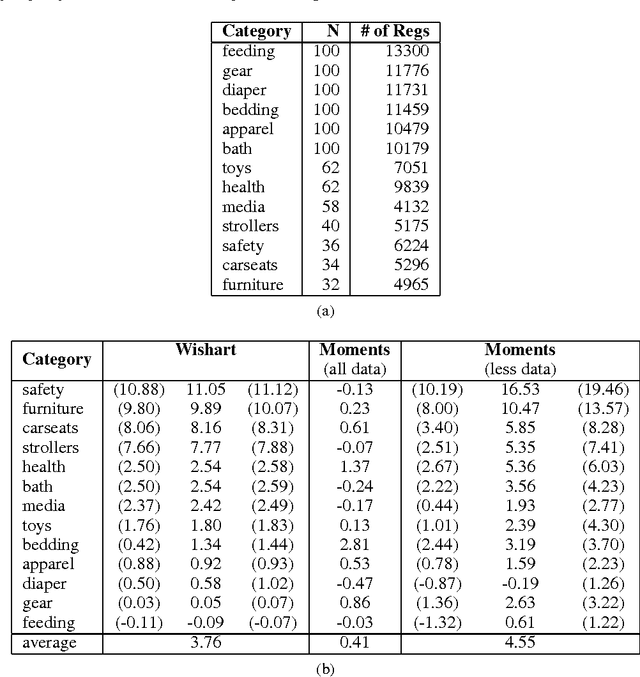
Differential privacy is often studied under two different models of neighboring datasets: the add-remove model and the swap model. While the swap model is used extensively in the academic literature, many practical libraries use the more conservative add-remove model. However, analysis under the add-remove model can be cumbersome, and obtaining results with tight constants requires some additional work. Here, we study the problem of one-dimensional mean estimation under the add-remove model of differential privacy. We propose a new algorithm and show that it is min-max optimal, that it has the correct constant in the leading term of the mean squared error, and that this constant is the same as the optimal algorithm in the swap model. Our results show that, for mean estimation, the add-remove and swap model give nearly identical error even though the add-remove model cannot treat the size of the dataset as public information. In addition, we demonstrate empirically that our proposed algorithm yields a factor of two improvement in mean squared error over algorithms often used in practice.

Subset-Based Instance Optimality in Private Estimation

We propose a new definition of instance optimality for differentially private estimation algorithms. Our definition requires an optimal algorithm to compete, simultaneously for every dataset $D$, with the best private benchmark algorithm that (a) knows $D$ in advance and (b) is evaluated by its worst-case performance on large subsets of $D$. That is, the benchmark algorithm need not perform well when potentially extreme points are added to $D$; it only has to handle the removal of a small number of real data points that already exist. This makes our benchmark significantly stronger than those proposed in prior work. We nevertheless show, for real-valued datasets, how to construct private algorithms that achieve our notion of instance optimality when estimating a broad class of dataset properties, including means, quantiles, and $\ell_p$-norm minimizers. For means in particular, we provide a detailed analysis and show that our algorithm simultaneously matches or exceeds the asymptotic performance of existing algorithms under a range of distributional assumptions.

Combining Public and Private Data

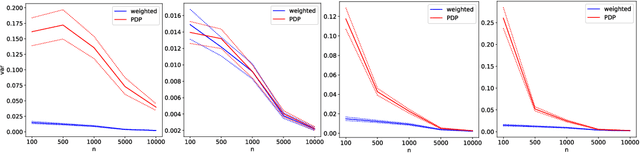
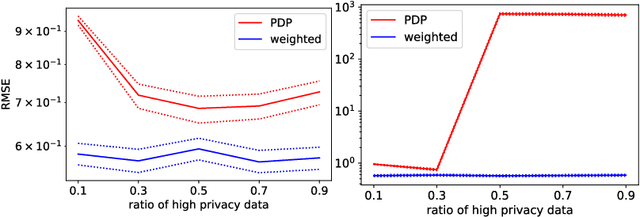
Differential privacy is widely adopted to provide provable privacy guarantees in data analysis. We consider the problem of combining public and private data (and, more generally, data with heterogeneous privacy needs) for estimating aggregate statistics. We introduce a mixed estimator of the mean optimized to minimize the variance. We argue that our mechanism is preferable to techniques that preserve the privacy of individuals by subsampling data proportionally to the privacy needs of users. Similarly, we present a mixed median estimator based on the exponential mechanism. We compare our mechanisms to the methods proposed in Jorgensen et al. [2015]. Our experiments provide empirical evidence that our mechanisms often outperform the baseline methods.

Learning with User-Level Privacy

We propose and analyze algorithms to solve a range of learning tasks under user-level differential privacy constraints. Rather than guaranteeing only the privacy of individual samples, user-level DP protects a user's entire contribution ($m \ge 1$ samples), providing more stringent but more realistic protection against information leaks. We show that for high-dimensional mean estimation, empirical risk minimization with smooth losses, stochastic convex optimization, and learning hypothesis class with finite metric entropy, the privacy cost decreases as $O(1/\sqrt{m})$ as users provide more samples. In contrast, when increasing the number of users $n$, the privacy cost decreases at a faster $O(1/n)$ rate. We complement these results with lower bounds showing the worst-case optimality of our algorithm for mean estimation and stochastic convex optimization. Our algorithms rely on novel techniques for private mean estimation in arbitrary dimension with error scaling as the concentration radius $\tau$ of the distribution rather than the entire range. Under uniform convergence, we derive an algorithm that privately answers a sequence of $K$ adaptively chosen queries with privacy cost proportional to $\tau$, and apply it to solve the learning tasks we consider.

Differentially Private Quantiles

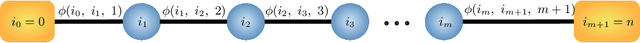
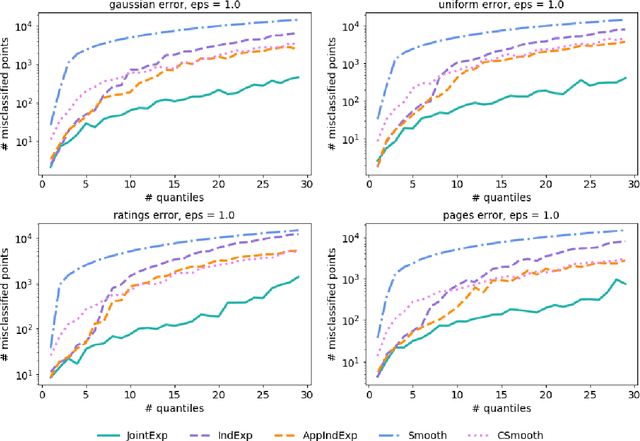
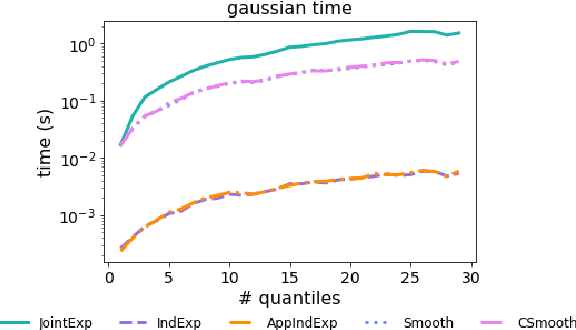
Quantiles are often used for summarizing and understanding data. If that data is sensitive, it may be necessary to compute quantiles in a way that is differentially private, providing theoretical guarantees that the result does not reveal private information. However, in the common case where multiple quantiles are needed, existing differentially private algorithms scale poorly: they compute each quantile individually, splitting their privacy budget and thus decreasing accuracy. In this work we propose an instance of the exponential mechanism that simultaneously estimates $m$ quantiles from $n$ data points while guaranteeing differential privacy. The utility function is carefully structured to allow for an efficient implementation that avoids exponential dependence on $m$ and returns estimates of all $m$ quantiles in time $O(mn^2 + m^2n)$. Experiments show that our method significantly outperforms the current state of the art on both real and synthetic data while remaining efficient enough to be practical.

Diversifying Sparsity Using Variational Determinantal Point Processes

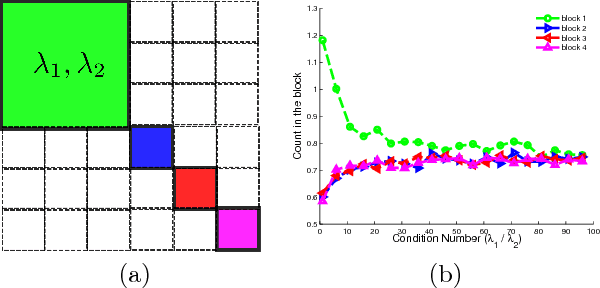
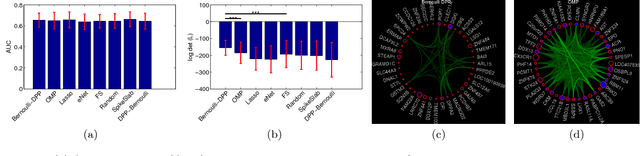
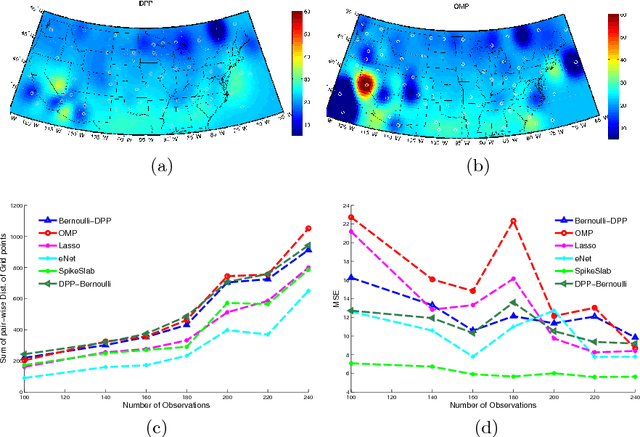
We propose a novel diverse feature selection method based on determinantal point processes (DPPs). Our model enables one to flexibly define diversity based on the covariance of features (similar to orthogonal matching pursuit) or alternatively based on side information. We introduce our approach in the context of Bayesian sparse regression, employing a DPP as a variational approximation to the true spike and slab posterior distribution. We subsequently show how this variational DPP approximation generalizes and extends mean-field approximation, and can be learned efficiently by exploiting the fast sampling properties of DPPs. Our motivating application comes from bioinformatics, where we aim to identify a diverse set of genes whose expression profiles predict a tumor type where the diversity is defined with respect to a gene-gene interaction network. We also explore an application in spatial statistics. In both cases, we demonstrate that the proposed method yields significantly more diverse feature sets than classic sparse methods, without compromising accuracy.

Expectation-Maximization for Learning Determinantal Point Processes

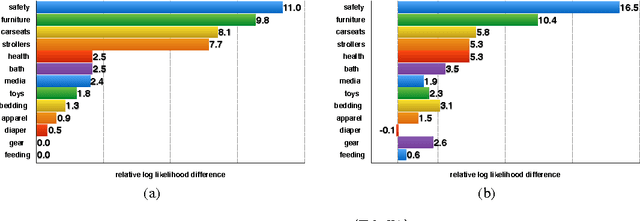
A determinantal point process (DPP) is a probabilistic model of set diversity compactly parameterized by a positive semi-definite kernel matrix. To fit a DPP to a given task, we would like to learn the entries of its kernel matrix by maximizing the log-likelihood of the available data. However, log-likelihood is non-convex in the entries of the kernel matrix, and this learning problem is conjectured to be NP-hard. Thus, previous work has instead focused on more restricted convex learning settings: learning only a single weight for each row of the kernel matrix, or learning weights for a linear combination of DPPs with fixed kernel matrices. In this work we propose a novel algorithm for learning the full kernel matrix. By changing the kernel parameterization from matrix entries to eigenvalues and eigenvectors, and then lower-bounding the likelihood in the manner of expectation-maximization algorithms, we obtain an effective optimization procedure. We test our method on a real-world product recommendation task, and achieve relative gains of up to 16.5% in test log-likelihood compared to the naive approach of maximizing likelihood by projected gradient ascent on the entries of the kernel matrix.

Determinantal point processes for machine learning

Determinantal point processes (DPPs) are elegant probabilistic models of repulsion that arise in quantum physics and random matrix theory. In contrast to traditional structured models like Markov random fields, which become intractable and hard to approximate in the presence of negative correlations, DPPs offer efficient and exact algorithms for sampling, marginalization, conditioning, and other inference tasks. We provide a gentle introduction to DPPs, focusing on the intuitions, algorithms, and extensions that are most relevant to the machine learning community, and show how DPPs can be applied to real-world applications like finding diverse sets of high-quality search results, building informative summaries by selecting diverse sentences from documents, modeling non-overlapping human poses in images or video, and automatically building timelines of important news stories.

Markov Determinantal Point Processes

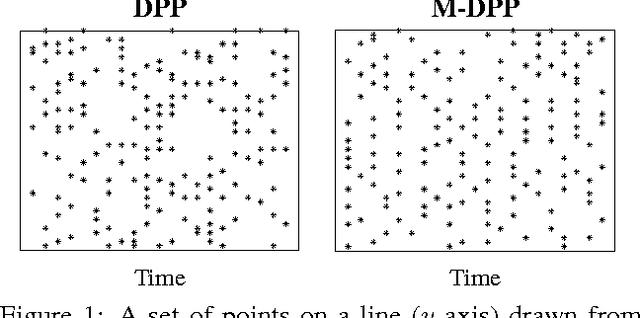
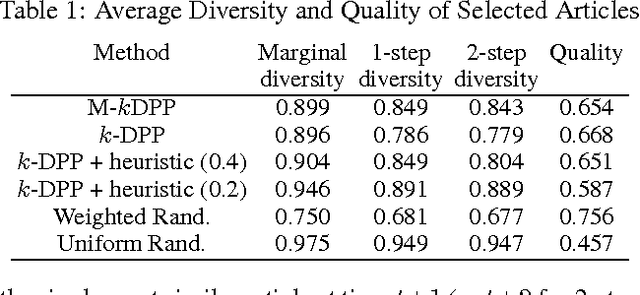
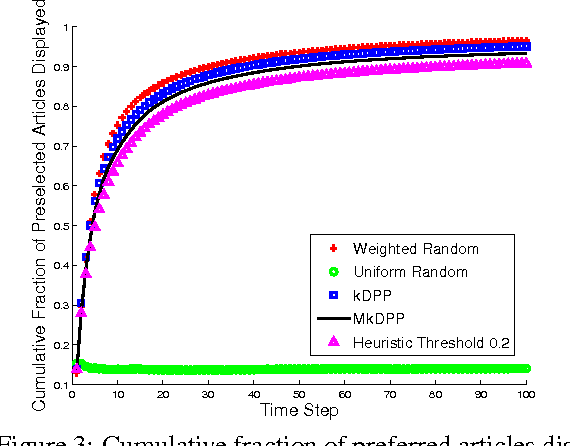
A determinantal point process (DPP) is a random process useful for modeling the combinatorial problem of subset selection. In particular, DPPs encourage a random subset Y to contain a diverse set of items selected from a base set Y. For example, we might use a DPP to display a set of news headlines that are relevant to a user's interests while covering a variety of topics. Suppose, however, that we are asked to sequentially select multiple diverse sets of items, for example, displaying new headlines day-by-day. We might want these sets to be diverse not just individually but also through time, offering headlines today that are unlike the ones shown yesterday. In this paper, we construct a Markov DPP (M-DPP) that models a sequence of random sets {Yt}. The proposed M-DPP defines a stationary process that maintains DPP margins. Crucially, the induced union process Zt = Yt u Yt-1 is also marginally DPP-distributed. Jointly, these properties imply that the sequence of random sets are encouraged to be diverse both at a given time step as well as across time steps. We describe an exact, efficient sampling procedure, and a method for incrementally learning a quality measure over items in the base set Y based on external preferences. We apply the M-DPP to the task of sequentially displaying diverse and relevant news articles to a user with topic preferences.

Learning Determinantal Point Processes

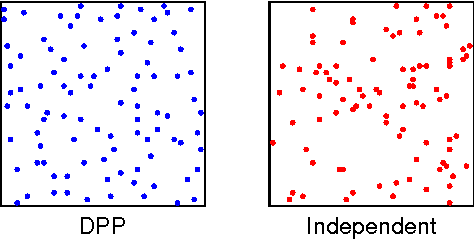
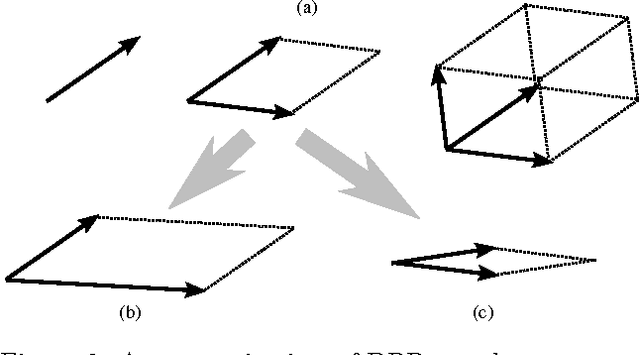
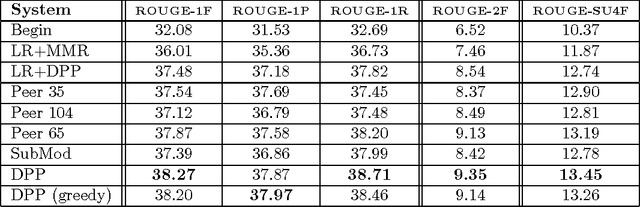
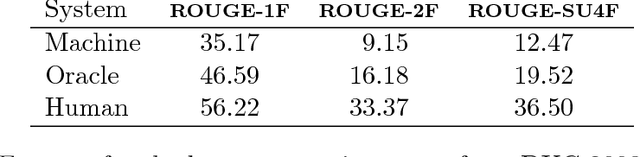
Determinantal point processes (DPPs), which arise in random matrix theory and quantum physics, are natural models for subset selection problems where diversity is preferred. Among many remarkable properties, DPPs offer tractable algorithms for exact inference, including computing marginal probabilities and sampling; however, an important open question has been how to learn a DPP from labeled training data. In this paper we propose a natural feature-based parameterization of conditional DPPs, and show how it leads to a convex and efficient learning formulation. We analyze the relationship between our model and binary Markov random fields with repulsive potentials, which are qualitatively similar but computationally intractable. Finally, we apply our approach to the task of extractive summarization, where the goal is to choose a small subset of sentences conveying the most important information from a set of documents. In this task there is a fundamental tradeoff between sentences that are highly relevant to the collection as a whole, and sentences that are diverse and not repetitive. Our parameterization allows us to naturally balance these two characteristics. We evaluate our system on data from the DUC 2003/04 multi-document summarization task, achieving state-of-the-art results.