The Vizier Gaussian Process Bandit Algorithm

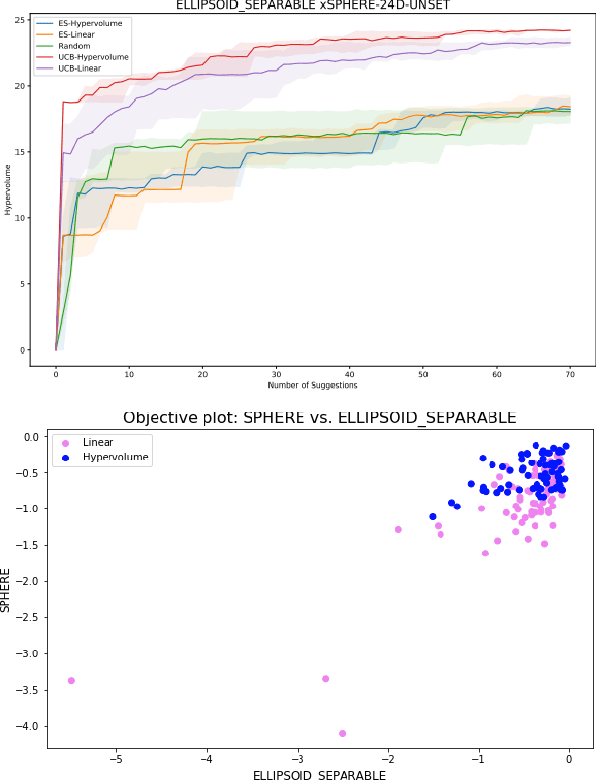
Google Vizier has performed millions of optimizations and accelerated numerous research and production systems at Google, demonstrating the success of Bayesian optimization as a large-scale service. Over multiple years, its algorithm has been improved considerably, through the collective experiences of numerous research efforts and user feedback. In this technical report, we discuss the implementation details and design choices of the current default algorithm provided by Open Source Vizier. Our experiments on standardized benchmarks reveal its robustness and versatility against well-established industry baselines on multiple practical modes.

SmartChoices: Augmenting Software with Learned Implementations

We are living in a golden age of machine learning. Powerful models are being trained to perform many tasks far better than is possible using traditional software engineering approaches alone. However, developing and deploying those models in existing software systems remains difficult. In this paper we present SmartChoices, a novel approach to incorporating machine learning into mature software stacks easily, safely, and effectively. We explain the overall design philosophy and present case studies using SmartChoices within large scale industrial systems.

Open Source Vizier: Distributed Infrastructure and API for Reliable and Flexible Blackbox Optimization

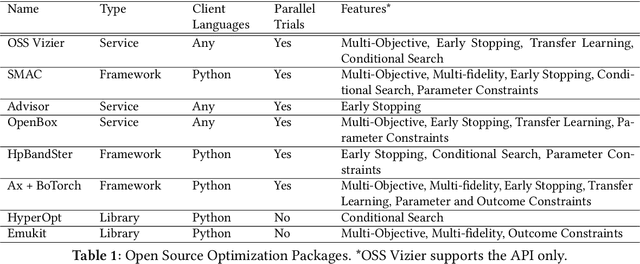
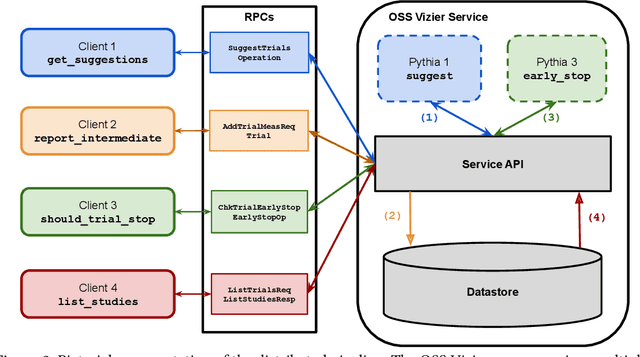
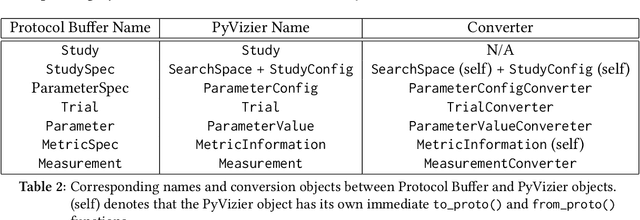
Vizier is the de-facto blackbox and hyperparameter optimization service across Google, having optimized some of Google's largest products and research efforts. To operate at the scale of tuning thousands of users' critical systems, Google Vizier solved key design challenges in providing multiple different features, while remaining fully fault-tolerant. In this paper, we introduce Open Source (OSS) Vizier, a standalone Python-based interface for blackbox optimization and research, based on the Google-internal Vizier infrastructure and framework. OSS Vizier provides an API capable of defining and solving a wide variety of optimization problems, including multi-metric, early stopping, transfer learning, and conditional search. Furthermore, it is designed to be a distributed system that assures reliability, and allows multiple parallel evaluations of the user's objective function. The flexible RPC-based infrastructure allows users to access OSS Vizier from binaries written in any language. OSS Vizier also provides a back-end ("Pythia") API that gives algorithm authors a way to interface new algorithms with the core OSS Vizier system. OSS Vizier is available at https://github.com/google/vizier.

Random Hypervolume Scalarizations for Provable Multi-Objective Black Box Optimization

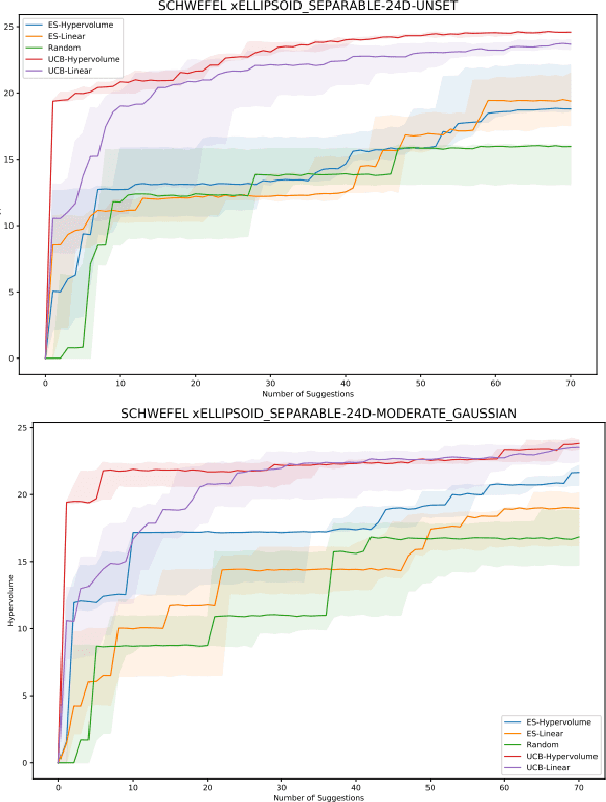
Single-objective black box optimization (also known as zeroth-order optimization) is the process of minimizing a scalar objective $f(x)$, given evaluations at adaptively chosen inputs $x$. In this paper, we consider multi-objective optimization, where $f(x)$ outputs a vector of possibly competing objectives and the goal is to converge to the Pareto frontier. Quantitatively, we wish to maximize the standard hypervolume indicator metric, which measures the dominated hypervolume of the entire set of chosen inputs. In this paper, we introduce a novel scalarization function, which we term the hypervolume scalarization, and show that drawing random scalarizations from an appropriately chosen distribution can be used to efficiently approximate the hypervolume indicator metric. We utilize this connection to show that Bayesian optimization with our scalarization via common acquisition functions, such as Thompson Sampling or Upper Confidence Bound, provably converges to the whole Pareto frontier by deriving tight hypervolume regret bounds on the order of $\widetilde{O}(\sqrt{T})$. Furthermore, we highlight the general utility of our scalarization framework by showing that any provably convergent single-objective optimization process can be effortlessly converted to a multi-objective optimization process with provable convergence guarantees.

Gradientless Descent: High-Dimensional Zeroth-Order Optimization

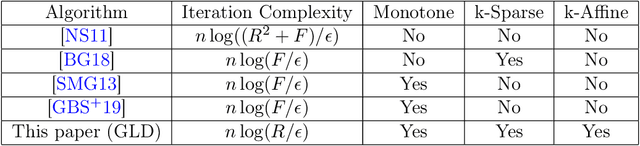
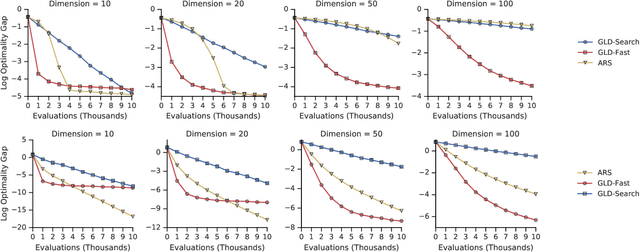
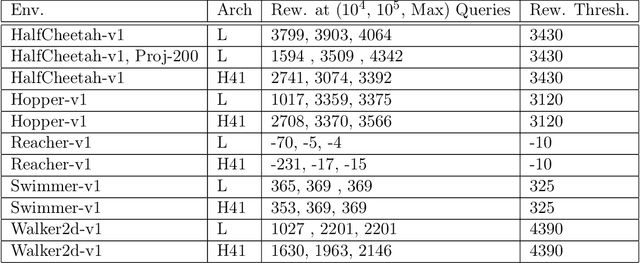
Zeroth-order optimization is the process of minimizing an objective $f(x)$, given oracle access to evaluations at adaptively chosen inputs $x$. In this paper, we present two simple yet powerful GradientLess Descent (GLD) algorithms that do not rely on an underlying gradient estimate and are numerically stable. We analyze our algorithm from a novel geometric perspective and present a novel analysis that shows convergence within an $\epsilon$-ball of the optimum in $O(kQ\log(n)\log(R/\epsilon))$ evaluations, for any monotone transform of a smooth and strongly convex objective with latent dimension $k < n$, where the input dimension is $n$, $R$ is the diameter of the input space and $Q$ is the condition number. Our rates are the first of its kind to be both 1) poly-logarithmically dependent on dimensionality and 2) invariant under monotone transformations. We further leverage our geometric perspective to show that our analysis is optimal. Both monotone invariance and its ability to utilize a low latent dimensionality are key to the empirical success of our algorithms, as demonstrated on BBOB and MuJoCo benchmarks.

Adaptive Submodularity: Theory and Applications in Active Learning and Stochastic Optimization

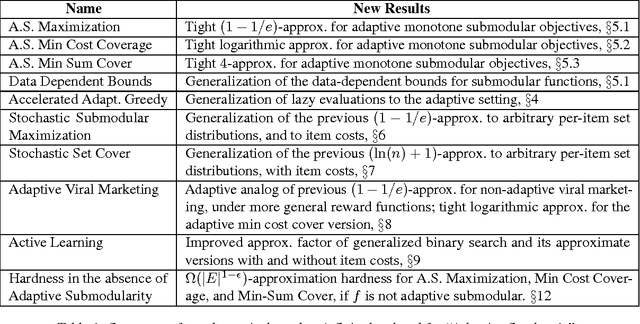
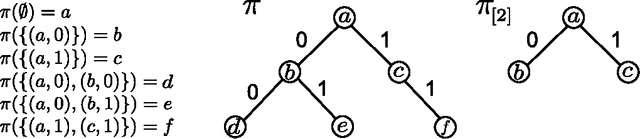
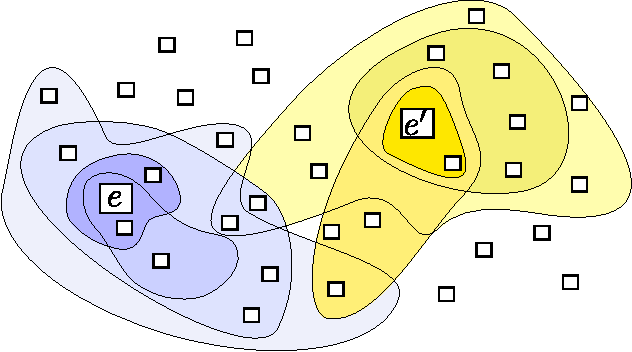
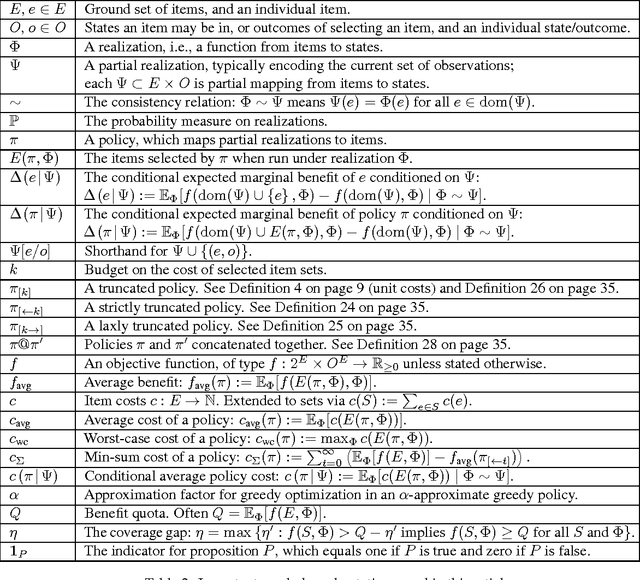
Solving stochastic optimization problems under partial observability, where one needs to adaptively make decisions with uncertain outcomes, is a fundamental but notoriously difficult challenge. In this paper, we introduce the concept of adaptive submodularity, generalizing submodular set functions to adaptive policies. We prove that if a problem satisfies this property, a simple adaptive greedy algorithm is guaranteed to be competitive with the optimal policy. In addition to providing performance guarantees for both stochastic maximization and coverage, adaptive submodularity can be exploited to drastically speed up the greedy algorithm by using lazy evaluations. We illustrate the usefulness of the concept by giving several examples of adaptive submodular objectives arising in diverse applications including sensor placement, viral marketing and active learning. Proving adaptive submodularity for these problems allows us to recover existing results in these applications as special cases, improve approximation guarantees and handle natural generalizations.

Online Submodular Maximization under a Matroid Constraint with Application to Learning Assignments

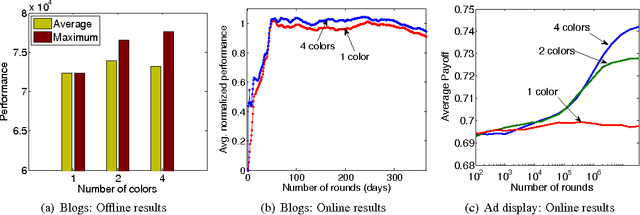
Which ads should we display in sponsored search in order to maximize our revenue? How should we dynamically rank information sources to maximize the value of the ranking? These applications exhibit strong diminishing returns: Redundancy decreases the marginal utility of each ad or information source. We show that these and other problems can be formalized as repeatedly selecting an assignment of items to positions to maximize a sequence of monotone submodular functions that arrive one by one. We present an efficient algorithm for this general problem and analyze it in the no-regret model. Our algorithm possesses strong theoretical guarantees, such as a performance ratio that converges to the optimal constant of 1 - 1/e. We empirically evaluate our algorithm on two real-world online optimization problems on the web: ad allocation with submodular utilities, and dynamically ranking blogs to detect information cascades. Finally, we present a second algorithm that handles the more general case in which the feasible sets are given by a matroid constraint, while still maintaining a 1 - 1/e asymptotic performance ratio.

Near-Optimal Bayesian Active Learning with Noisy Observations

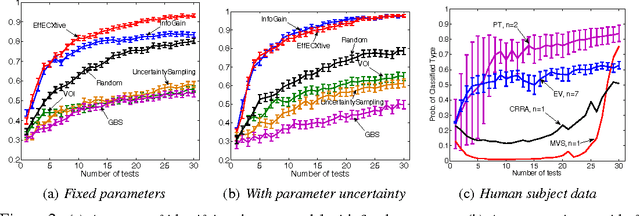
We tackle the fundamental problem of Bayesian active learning with noise, where we need to adaptively select from a number of expensive tests in order to identify an unknown hypothesis sampled from a known prior distribution. In the case of noise-free observations, a greedy algorithm called generalized binary search (GBS) is known to perform near-optimally. We show that if the observations are noisy, perhaps surprisingly, GBS can perform very poorly. We develop EC2, a novel, greedy active learning algorithm and prove that it is competitive with the optimal policy, thus obtaining the first competitiveness guarantees for Bayesian active learning with noisy observations. Our bounds rely on a recently discovered diminishing returns property called adaptive submodularity, generalizing the classical notion of submodular set functions to adaptive policies. Our results hold even if the tests have non-uniform cost and their noise is correlated. We also propose EffECXtive, a particularly fast approximation of EC2, and evaluate it on a Bayesian experimental design problem involving human subjects, intended to tease apart competing economic theories of how people make decisions under uncertainty.

Large-Scale Learning with Less RAM via Randomization

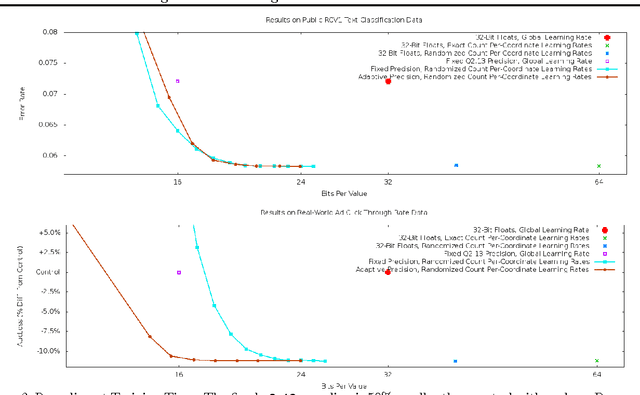
We reduce the memory footprint of popular large-scale online learning methods by projecting our weight vector onto a coarse discrete set using randomized rounding. Compared to standard 32-bit float encodings, this reduces RAM usage by more than 50% during training and by up to 95% when making predictions from a fixed model, with almost no loss in accuracy. We also show that randomized counting can be used to implement per-coordinate learning rates, improving model quality with little additional RAM. We prove these memory-saving methods achieve regret guarantees similar to their exact variants. Empirical evaluation confirms excellent performance, dominating standard approaches across memory versus accuracy tradeoffs.

Adaptive Submodular Optimization under Matroid Constraints

Many important problems in discrete optimization require maximization of a monotonic submodular function subject to matroid constraints. For these problems, a simple greedy algorithm is guaranteed to obtain near-optimal solutions. In this article, we extend this classic result to a general class of adaptive optimization problems under partial observability, where each choice can depend on observations resulting from past choices. Specifically, we prove that a natural adaptive greedy algorithm provides a $1/(p+1)$ approximation for the problem of maximizing an adaptive monotone submodular function subject to $p$ matroid constraints, and more generally over arbitrary $p$-independence systems. We illustrate the usefulness of our result on a complex adaptive match-making application.