Trajectory of Mini-Batch Momentum: Batch Size Saturation and Convergence in High Dimensions

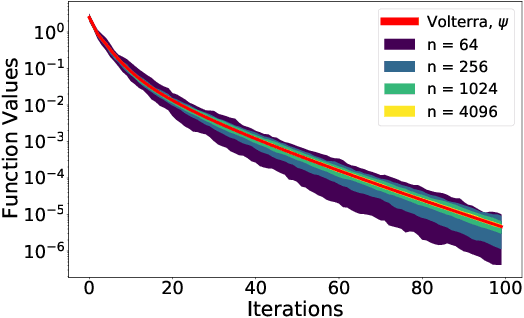
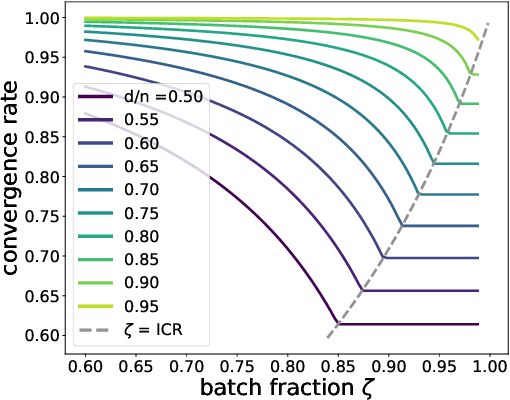
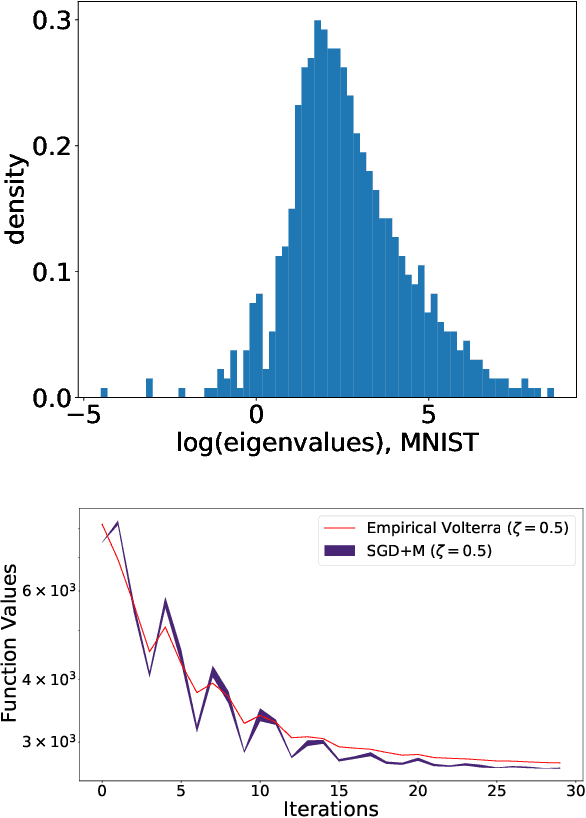
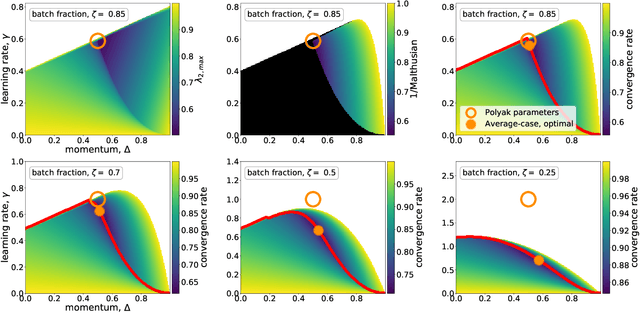
We analyze the dynamics of large batch stochastic gradient descent with momentum (SGD+M) on the least squares problem when both the number of samples and dimensions are large. In this setting, we show that the dynamics of SGD+M converge to a deterministic discrete Volterra equation as dimension increases, which we analyze. We identify a stability measurement, the implicit conditioning ratio (ICR), which regulates the ability of SGD+M to accelerate the algorithm. When the batch size exceeds this ICR, SGD+M converges linearly at a rate of $\mathcal{O}(1/\sqrt{\kappa})$, matching optimal full-batch momentum (in particular performing as well as a full-batch but with a fraction of the size). For batch sizes smaller than the ICR, in contrast, SGD+M has rates that scale like a multiple of the single batch SGD rate. We give explicit choices for the learning rate and momentum parameter in terms of the Hessian spectra that achieve this performance.

SGD in the Large: Average-case Analysis, Asymptotics, and Stepsize Criticality

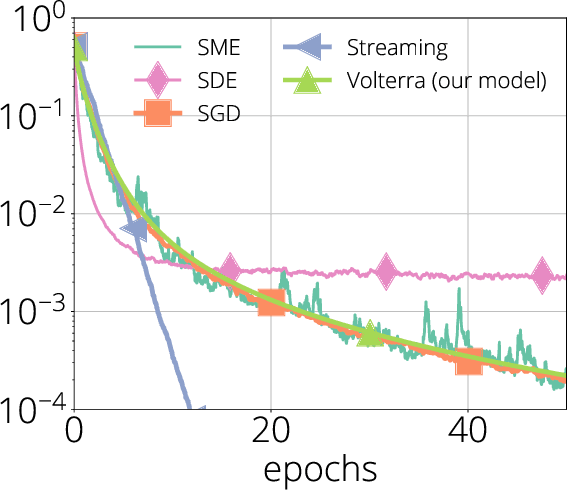
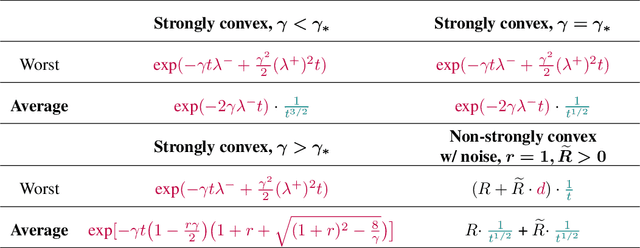
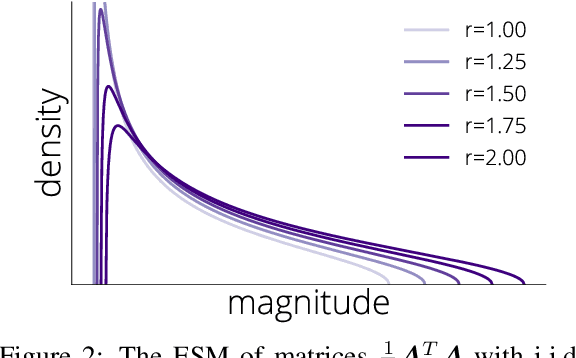
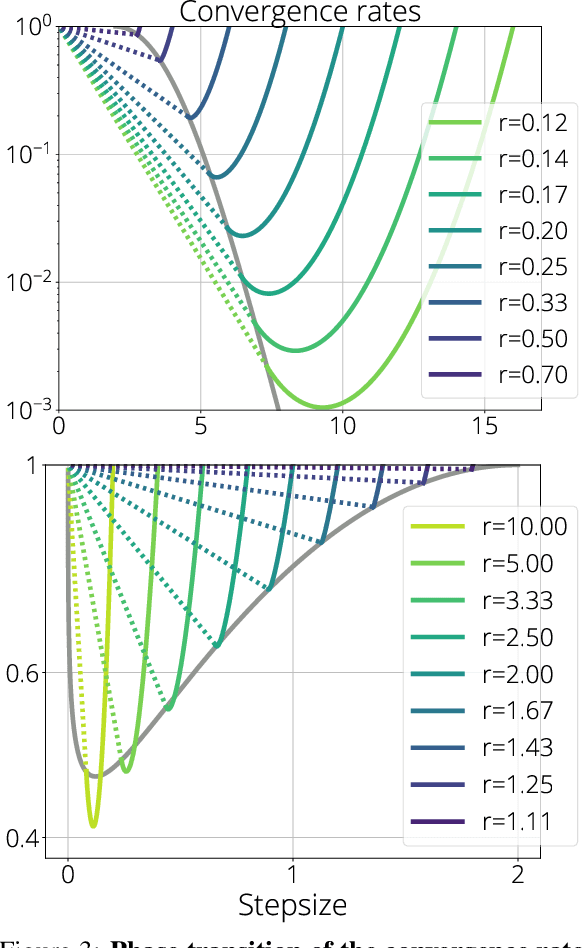
We propose a new framework, inspired by random matrix theory, for analyzing the dynamics of stochastic gradient descent (SGD) when both number of samples and dimensions are large. This framework applies to any fixed stepsize and the finite sum setting. Using this new framework, we show that the dynamics of SGD on a least squares problem with random data become deterministic in the large sample and dimensional limit. Furthermore, the limiting dynamics are governed by a Volterra integral equation. This model predicts that SGD undergoes a phase transition at an explicitly given critical stepsize that ultimately affects its convergence rate, which we also verify experimentally. Finally, when input data is isotropic, we provide explicit expressions for the dynamics and average-case convergence rates (i.e., the complexity of an algorithm averaged over all possible inputs). These rates show significant improvement over the worst-case complexities.