Attention layers provably solve single-location regression

Attention-based models, such as Transformer, excel across various tasks but lack a comprehensive theoretical understanding, especially regarding token-wise sparsity and internal linear representations. To address this gap, we introduce the single-location regression task, where only one token in a sequence determines the output, and its position is a latent random variable, retrievable via a linear projection of the input. To solve this task, we propose a dedicated predictor, which turns out to be a simplified version of a non-linear self-attention layer. We study its theoretical properties, by showing its asymptotic Bayes optimality and analyzing its training dynamics. In particular, despite the non-convex nature of the problem, the predictor effectively learns the underlying structure. This work highlights the capacity of attention mechanisms to handle sparse token information and internal linear structures.

Deep linear networks for regression are implicitly regularized towards flat minima

The largest eigenvalue of the Hessian, or sharpness, of neural networks is a key quantity to understand their optimization dynamics. In this paper, we study the sharpness of deep linear networks for overdetermined univariate regression. Minimizers can have arbitrarily large sharpness, but not an arbitrarily small one. Indeed, we show a lower bound on the sharpness of minimizers, which grows linearly with depth. We then study the properties of the minimizer found by gradient flow, which is the limit of gradient descent with vanishing learning rate. We show an implicit regularization towards flat minima: the sharpness of the minimizer is no more than a constant times the lower bound. The constant depends on the condition number of the data covariance matrix, but not on width or depth. This result is proven both for a small-scale initialization and a residual initialization. Results of independent interest are shown in both cases. For small-scale initialization, we show that the learned weight matrices are approximately rank-one and that their singular vectors align. For residual initialization, convergence of the gradient flow for a Gaussian initialization of the residual network is proven. Numerical experiments illustrate our results and connect them to gradient descent with non-vanishing learning rate.

Implicit Diffusion: Efficient Optimization through Stochastic Sampling

We present a new algorithm to optimize distributions defined implicitly by parameterized stochastic diffusions. Doing so allows us to modify the outcome distribution of sampling processes by optimizing over their parameters. We introduce a general framework for first-order optimization of these processes, that performs jointly, in a single loop, optimization and sampling steps. This approach is inspired by recent advances in bilevel optimization and automatic implicit differentiation, leveraging the point of view of sampling as optimization over the space of probability distributions. We provide theoretical guarantees on the performance of our method, as well as experimental results demonstrating its effectiveness in real-world settings.

Implicit regularization of deep residual networks towards neural ODEs

Residual neural networks are state-of-the-art deep learning models. Their continuous-depth analog, neural ordinary differential equations (ODEs), are also widely used. Despite their success, the link between the discrete and continuous models still lacks a solid mathematical foundation. In this article, we take a step in this direction by establishing an implicit regularization of deep residual networks towards neural ODEs, for nonlinear networks trained with gradient flow. We prove that if the network is initialized as a discretization of a neural ODE, then such a discretization holds throughout training. Our results are valid for a finite training time, and also as the training time tends to infinity provided that the network satisfies a Polyak-Lojasiewicz condition. Importantly, this condition holds for a family of residual networks where the residuals are two-layer perceptrons with an overparameterization in width that is only linear, and implies the convergence of gradient flow to a global minimum. Numerical experiments illustrate our results.

Generalization bounds for neural ordinary differential equations and deep residual networks

Neural ordinary differential equations (neural ODEs) are a popular family of continuous-depth deep learning models. In this work, we consider a large family of parameterized ODEs with continuous-in-time parameters, which include time-dependent neural ODEs. We derive a generalization bound for this class by a Lipschitz-based argument. By leveraging the analogy between neural ODEs and deep residual networks, our approach yields in particular a generalization bound for a class of deep residual networks. The bound involves the magnitude of the difference between successive weight matrices. We illustrate numerically how this quantity affects the generalization capability of neural networks.

Leveraging the two timescale regime to demonstrate convergence of neural networks

We study the training dynamics of shallow neural networks, in a two-timescale regime in which the stepsizes for the inner layer are much smaller than those for the outer layer. In this regime, we prove convergence of the gradient flow to a global optimum of the non-convex optimization problem in a simple univariate setting. The number of neurons need not be asymptotically large for our result to hold, distinguishing our result from popular recent approaches such as the neural tangent kernel or mean-field regimes. Experimental illustration is provided, showing that the stochastic gradient descent behaves according to our description of the gradient flow and thus converges to a global optimum in the two-timescale regime, but can fail outside of this regime.

Scaling ResNets in the Large-depth Regime

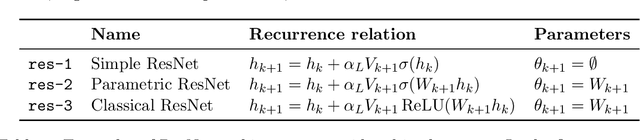
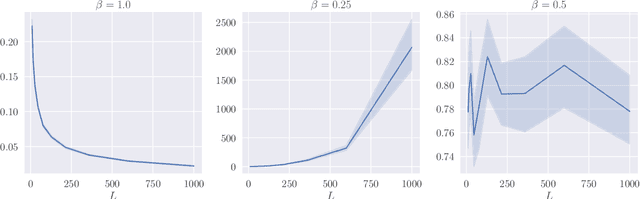
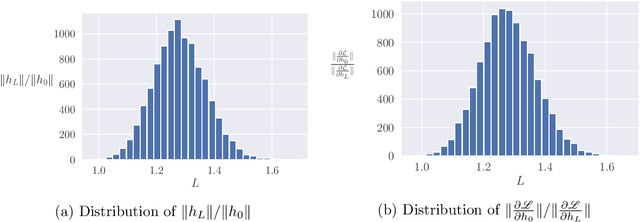
Deep ResNets are recognized for achieving state-of-the-art results in complex machine learning tasks. However, the remarkable performance of these architectures relies on a training procedure that needs to be carefully crafted to avoid vanishing or exploding gradients, particularly as the depth $L$ increases. No consensus has been reached on how to mitigate this issue, although a widely discussed strategy consists in scaling the output of each layer by a factor $\alpha_L$. We show in a probabilistic setting that with standard i.i.d. initializations, the only non-trivial dynamics is for $\alpha_L = 1/\sqrt{L}$ (other choices lead either to explosion or to identity mapping). This scaling factor corresponds in the continuous-time limit to a neural stochastic differential equation, contrarily to a widespread interpretation that deep ResNets are discretizations of neural ordinary differential equations. By contrast, in the latter regime, stability is obtained with specific correlated initializations and $\alpha_L = 1/L$. Our analysis suggests a strong interplay between scaling and regularity of the weights as a function of the layer index. Finally, in a series of experiments, we exhibit a continuous range of regimes driven by these two parameters, which jointly impact performance before and after training.

Structured Context and High-Coverage Grammar for Conversational Question Answering over Knowledge Graphs

We tackle the problem of weakly-supervised conversational Question Answering over large Knowledge Graphs using a neural semantic parsing approach. We introduce a new Logical Form (LF) grammar that can model a wide range of queries on the graph while remaining sufficiently simple to generate supervision data efficiently. Our Transformer-based model takes a JSON-like structure as input, allowing us to easily incorporate both Knowledge Graph and conversational contexts. This structured input is transformed to lists of embeddings and then fed to standard attention layers. We validate our approach, both in terms of grammar coverage and LF execution accuracy, on two publicly available datasets, CSQA and ConvQuestions, both grounded in Wikidata. On CSQA, our approach increases the coverage from $80\%$ to $96.2\%$, and the LF execution accuracy from $70.6\%$ to $75.6\%$, with respect to previous state-of-the-art results. On ConvQuestions, we achieve competitive results with respect to the state-of-the-art.

Framing RNN as a kernel method: A neural ODE approach

Building on the interpretation of a recurrent neural network (RNN) as a continuous-time neural differential equation, we show, under appropriate conditions, that the solution of a RNN can be viewed as a linear function of a specific feature set of the input sequence, known as the signature. This connection allows us to frame a RNN as a kernel method in a suitable reproducing kernel Hilbert space. As a consequence, we obtain theoretical guarantees on generalization and stability for a large class of recurrent networks. Our results are illustrated on simulated datasets.