Eigenvalue distribution of the Neural Tangent Kernel in the quadratic scaling

We compute the asymptotic eigenvalue distribution of the neural tangent kernel of a two-layer neural network under a specific scaling of dimension. Namely, if $X\in\mathbb{R}^{n\times d}$ is an i.i.d random matrix, $W\in\mathbb{R}^{d\times p}$ is an i.i.d $\mathcal{N}(0,1)$ matrix and $D\in\mathbb{R}^{p\times p}$ is a diagonal matrix with i.i.d bounded entries, we consider the matrix \[ \mathrm{NTK} = \frac{1}{d}XX^\top \odot \frac{1}{p} \sigma'\left( \frac{1}{\sqrt{d}}XW \right)D^2 \sigma'\left( \frac{1}{\sqrt{d}}XW \right)^\top \] where $\sigma'$ is a pseudo-Lipschitz function applied entrywise and under the scaling $\frac{n}{dp}\to \gamma_1$ and $\frac{p}{d}\to \gamma_2$. We describe the asymptotic distribution as the free multiplicative convolution of the Marchenko--Pastur distribution with a deterministic distribution depending on $\sigma$ and $D$.

Dimension-adapted Momentum Outscales SGD

We investigate scaling laws for stochastic momentum algorithms with small batch on the power law random features model, parameterized by data complexity, target complexity, and model size. When trained with a stochastic momentum algorithm, our analysis reveals four distinct loss curve shapes determined by varying data-target complexities. While traditional stochastic gradient descent with momentum (SGD-M) yields identical scaling law exponents to SGD, dimension-adapted Nesterov acceleration (DANA) improves these exponents by scaling momentum hyperparameters based on model size and data complexity. This outscaling phenomenon, which also improves compute-optimal scaling behavior, is achieved by DANA across a broad range of data and target complexities, while traditional methods fall short. Extensive experiments on high-dimensional synthetic quadratics validate our theoretical predictions and large-scale text experiments with LSTMs show DANA's improved loss exponents over SGD hold in a practical setting.

Exact Risk Curves of signSGD in High-Dimensions: Quantifying Preconditioning and Noise-Compression Effects

In recent years, signSGD has garnered interest as both a practical optimizer as well as a simple model to understand adaptive optimizers like Adam. Though there is a general consensus that signSGD acts to precondition optimization and reshapes noise, quantitatively understanding these effects in theoretically solvable settings remains difficult. We present an analysis of signSGD in a high dimensional limit, and derive a limiting SDE and ODE to describe the risk. Using this framework we quantify four effects of signSGD: effective learning rate, noise compression, diagonal preconditioning, and gradient noise reshaping. Our analysis is consistent with experimental observations but moves beyond that by quantifying the dependence of these effects on the data and noise distributions. We conclude with a conjecture on how these results might be extended to Adam.

A Clipped Trip: the Dynamics of SGD with Gradient Clipping in High-Dimensions

The success of modern machine learning is due in part to the adaptive optimization methods that have been developed to deal with the difficulties of training large models over complex datasets. One such method is gradient clipping: a practical procedure with limited theoretical underpinnings. In this work, we study clipping in a least squares problem under streaming SGD. We develop a theoretical analysis of the learning dynamics in the limit of large intrinsic dimension-a model and dataset dependent notion of dimensionality. In this limit we find a deterministic equation that describes the evolution of the loss. We show that with Gaussian noise clipping cannot improve SGD performance. Yet, in other noisy settings, clipping can provide benefits with tuning of the clipping threshold. In these cases, clipping biases updates in a way beneficial to training which cannot be recovered by SGD under any schedule. We conclude with a discussion about the links between high-dimensional clipping and neural network training.

The High Line: Exact Risk and Learning Rate Curves of Stochastic Adaptive Learning Rate Algorithms

We develop a framework for analyzing the training and learning rate dynamics on a large class of high-dimensional optimization problems, which we call the high line, trained using one-pass stochastic gradient descent (SGD) with adaptive learning rates. We give exact expressions for the risk and learning rate curves in terms of a deterministic solution to a system of ODEs. We then investigate in detail two adaptive learning rates -- an idealized exact line search and AdaGrad-Norm -- on the least squares problem. When the data covariance matrix has strictly positive eigenvalues, this idealized exact line search strategy can exhibit arbitrarily slower convergence when compared to the optimal fixed learning rate with SGD. Moreover we exactly characterize the limiting learning rate (as time goes to infinity) for line search in the setting where the data covariance has only two distinct eigenvalues. For noiseless targets, we further demonstrate that the AdaGrad-Norm learning rate converges to a deterministic constant inversely proportional to the average eigenvalue of the data covariance matrix, and identify a phase transition when the covariance density of eigenvalues follows a power law distribution.

4+3 Phases of Compute-Optimal Neural Scaling Laws

We consider the three parameter solvable neural scaling model introduced by Maloney, Roberts, and Sully. The model has three parameters: data complexity, target complexity, and model-parameter-count. We use this neural scaling model to derive new predictions about the compute-limited, infinite-data scaling law regime. To train the neural scaling model, we run one-pass stochastic gradient descent on a mean-squared loss. We derive a representation of the loss curves which holds over all iteration counts and improves in accuracy as the model parameter count grows. We then analyze the compute-optimal model-parameter-count, and identify 4 phases (+3 subphases) in the data-complexity/target-complexity phase-plane. The phase boundaries are determined by the relative importance of model capacity, optimizer noise, and embedding of the features. We furthermore derive, with mathematical proof and extensive numerical evidence, the scaling-law exponents in all of these phases, in particular computing the optimal model-parameter-count as a function of floating point operation budget.

Hitting the High-Dimensional Notes: An ODE for SGD learning dynamics on GLMs and multi-index models

We analyze the dynamics of streaming stochastic gradient descent (SGD) in the high-dimensional limit when applied to generalized linear models and multi-index models (e.g. logistic regression, phase retrieval) with general data-covariance. In particular, we demonstrate a deterministic equivalent of SGD in the form of a system of ordinary differential equations that describes a wide class of statistics, such as the risk and other measures of sub-optimality. This equivalence holds with overwhelming probability when the model parameter count grows proportionally to the number of data. This framework allows us to obtain learning rate thresholds for stability of SGD as well as convergence guarantees. In addition to the deterministic equivalent, we introduce an SDE with a simplified diffusion coefficient (homogenized SGD) which allows us to analyze the dynamics of general statistics of SGD iterates. Finally, we illustrate this theory on some standard examples and show numerical simulations which give an excellent match to the theory.

Fitting an ellipsoid to a quadratic number of random points

We consider the problem $(\mathrm{P})$ of fitting $n$ standard Gaussian random vectors in $\mathbb{R}^d$ to the boundary of a centered ellipsoid, as $n, d \to \infty$. This problem is conjectured to have a sharp feasibility transition: for any $\varepsilon > 0$, if $n \leq (1 - \varepsilon) d^2 / 4$ then $(\mathrm{P})$ has a solution with high probability, while $(\mathrm{P})$ has no solutions with high probability if $n \geq (1 + \varepsilon) d^2 /4$. So far, only a trivial bound $n \geq d^2 / 2$ is known on the negative side, while the best results on the positive side assume $n \leq d^2 / \mathrm{polylog}(d)$. In this work, we improve over previous approaches using a key result of Bartl & Mendelson on the concentration of Gram matrices of random vectors under mild assumptions on their tail behavior. This allows us to give a simple proof that $(\mathrm{P})$ is feasible with high probability when $n \leq d^2 / C$, for a (possibly large) constant $C > 0$.

Implicit Regularization or Implicit Conditioning? Exact Risk Trajectories of SGD in High Dimensions

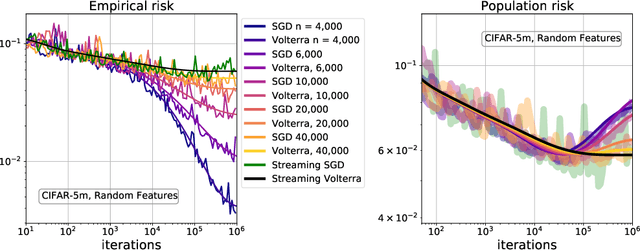
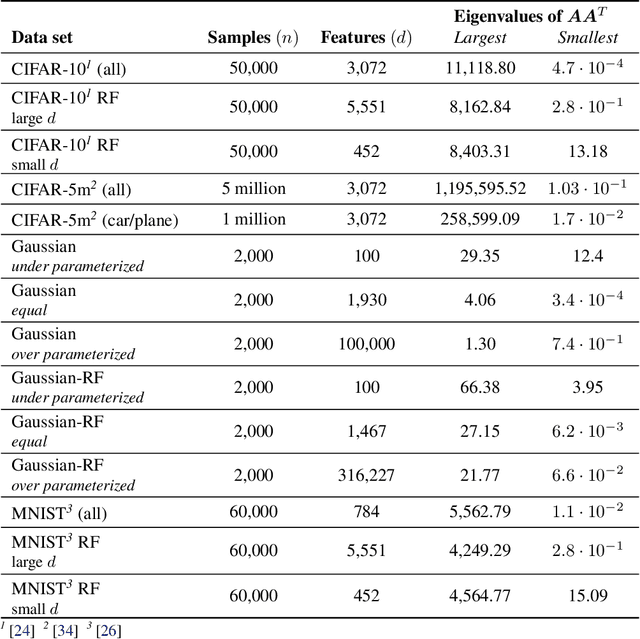
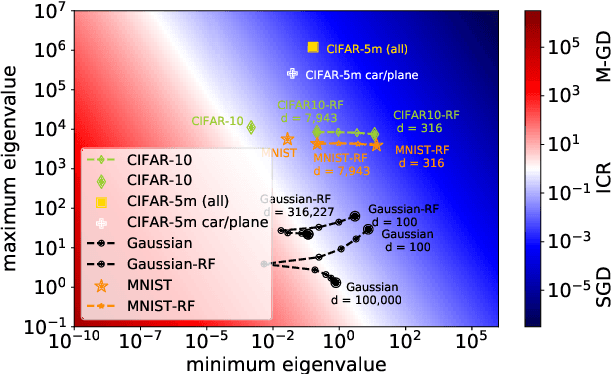
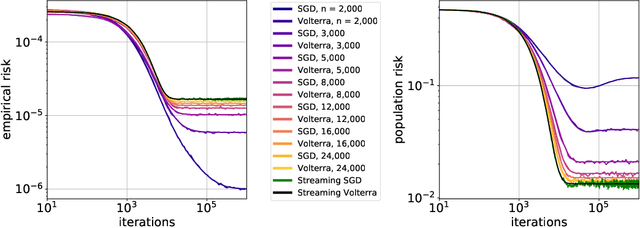
Stochastic gradient descent (SGD) is a pillar of modern machine learning, serving as the go-to optimization algorithm for a diverse array of problems. While the empirical success of SGD is often attributed to its computational efficiency and favorable generalization behavior, neither effect is well understood and disentangling them remains an open problem. Even in the simple setting of convex quadratic problems, worst-case analyses give an asymptotic convergence rate for SGD that is no better than full-batch gradient descent (GD), and the purported implicit regularization effects of SGD lack a precise explanation. In this work, we study the dynamics of multi-pass SGD on high-dimensional convex quadratics and establish an asymptotic equivalence to a stochastic differential equation, which we call homogenized stochastic gradient descent (HSGD), whose solutions we characterize explicitly in terms of a Volterra integral equation. These results yield precise formulas for the learning and risk trajectories, which reveal a mechanism of implicit conditioning that explains the efficiency of SGD relative to GD. We also prove that the noise from SGD negatively impacts generalization performance, ruling out the possibility of any type of implicit regularization in this context. Finally, we show how to adapt the HSGD formalism to include streaming SGD, which allows us to produce an exact prediction for the excess risk of multi-pass SGD relative to that of streaming SGD (bootstrap risk).

Trajectory of Mini-Batch Momentum: Batch Size Saturation and Convergence in High Dimensions

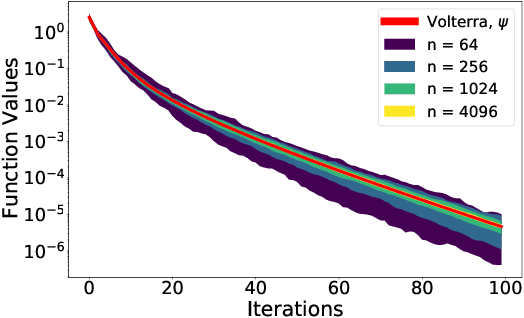
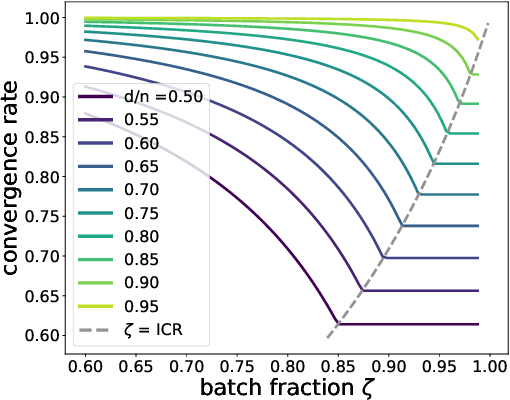
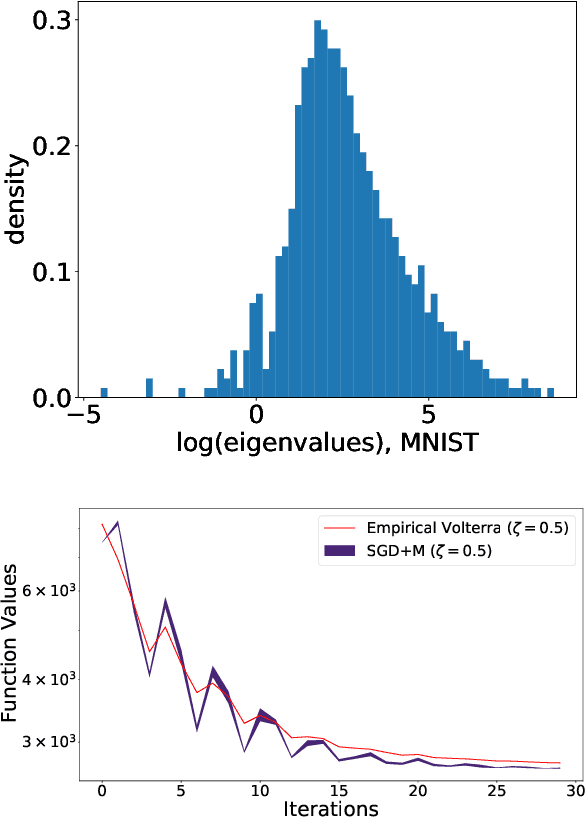
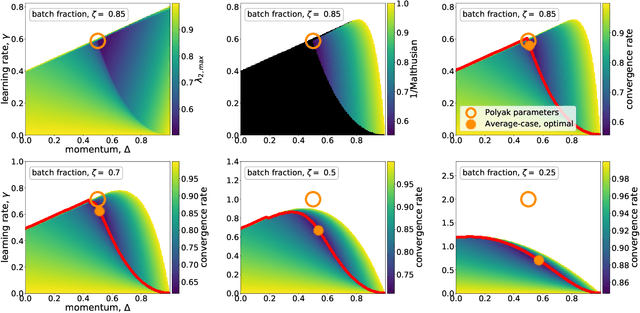
We analyze the dynamics of large batch stochastic gradient descent with momentum (SGD+M) on the least squares problem when both the number of samples and dimensions are large. In this setting, we show that the dynamics of SGD+M converge to a deterministic discrete Volterra equation as dimension increases, which we analyze. We identify a stability measurement, the implicit conditioning ratio (ICR), which regulates the ability of SGD+M to accelerate the algorithm. When the batch size exceeds this ICR, SGD+M converges linearly at a rate of $\mathcal{O}(1/\sqrt{\kappa})$, matching optimal full-batch momentum (in particular performing as well as a full-batch but with a fraction of the size). For batch sizes smaller than the ICR, in contrast, SGD+M has rates that scale like a multiple of the single batch SGD rate. We give explicit choices for the learning rate and momentum parameter in terms of the Hessian spectra that achieve this performance.