Do Transformer World Models Give Better Policy Gradients?

A natural approach for reinforcement learning is to predict future rewards by unrolling a neural network world model, and to backpropagate through the resulting computational graph to learn a policy. However, this method often becomes impractical for long horizons since typical world models induce hard-to-optimize loss landscapes. Transformers are known to efficiently propagate gradients over long horizons: could they be the solution to this problem? Surprisingly, we show that commonly-used transformer world models produce circuitous gradient paths, which can be detrimental to long-range policy gradients. To tackle this challenge, we propose a class of world models called Actions World Models (AWMs), designed to provide more direct routes for gradient propagation. We integrate such AWMs into a policy gradient framework that underscores the relationship between network architectures and the policy gradient updates they inherently represent. We demonstrate that AWMs can generate optimization landscapes that are easier to navigate even when compared to those from the simulator itself. This property allows transformer AWMs to produce better policies than competitive baselines in realistic long-horizon tasks.

Bridging State and History Representations: Understanding Self-Predictive RL

Representations are at the core of all deep reinforcement learning (RL) methods for both Markov decision processes (MDPs) and partially observable Markov decision processes (POMDPs). Many representation learning methods and theoretical frameworks have been developed to understand what constitutes an effective representation. However, the relationships between these methods and the shared properties among them remain unclear. In this paper, we show that many of these seemingly distinct methods and frameworks for state and history abstractions are, in fact, based on a common idea of self-predictive abstraction. Furthermore, we provide theoretical insights into the widely adopted objectives and optimization, such as the stop-gradient technique, in learning self-predictive representations. These findings together yield a minimalist algorithm to learn self-predictive representations for states and histories. We validate our theories by applying our algorithm to standard MDPs, MDPs with distractors, and POMDPs with sparse rewards. These findings culminate in a set of practical guidelines for RL practitioners.

Course Correcting Koopman Representations

Koopman representations aim to learn features of nonlinear dynamical systems (NLDS) which lead to linear dynamics in the latent space. Theoretically, such features can be used to simplify many problems in modeling and control of NLDS. In this work we study autoencoder formulations of this problem, and different ways they can be used to model dynamics, specifically for future state prediction over long horizons. We discover several limitations of predicting future states in the latent space and propose an inference-time mechanism, which we refer to as Periodic Reencoding, for faithfully capturing long term dynamics. We justify this method both analytically and empirically via experiments in low and high dimensional NLDS.

Reinforcement Learning for Classical Planning: Viewing Heuristics as Dense Reward Generators

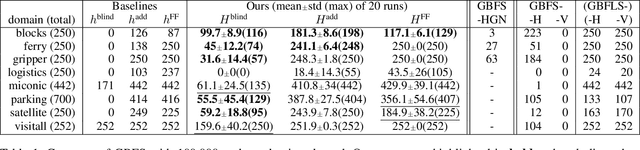
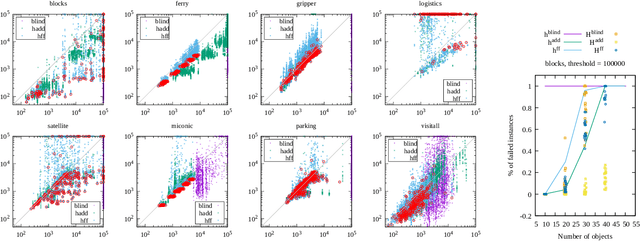
Recent advances in reinforcement learning (RL) have led to a growing interest in applying RL to classical planning domains or applying classical planning methods to some complex RL domains. However, the long-horizon goal-based problems found in classical planning lead to sparse rewards for RL, making direct application inefficient. In this paper, we propose to leverage domain-independent heuristic functions commonly used in the classical planning literature to improve the sample efficiency of RL. These classical heuristics act as dense reward generators to alleviate the sparse-rewards issue and enable our RL agent to learn domain-specific value functions as residuals on these heuristics, making learning easier. Correct application of this technique requires consolidating the discounted metric used in RL and the non-discounted metric used in heuristics. We implement the value functions using Neural Logic Machines, a neural network architecture designed for grounded first-order logic inputs. We demonstrate on several classical planning domains that using classical heuristics for RL allows for good sample efficiency compared to sparse-reward RL. We further show that our learned value functions generalize to novel problem instances in the same domain.

Batched Large-scale Bayesian Optimization in High-dimensional Spaces

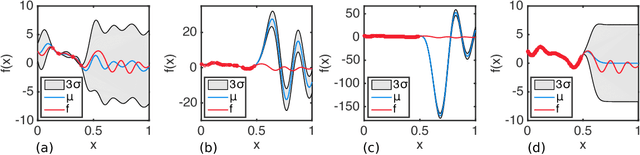
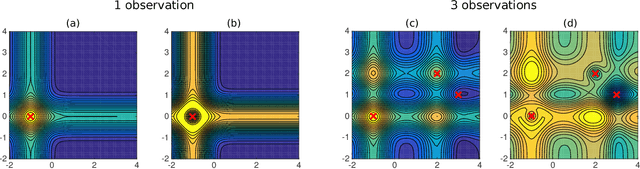
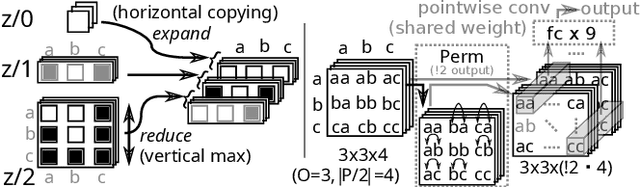
Bayesian optimization (BO) has become an effective approach for black-box function optimization problems when function evaluations are expensive and the optimum can be achieved within a relatively small number of queries. However, many cases, such as the ones with high-dimensional inputs, may require a much larger number of observations for optimization. Despite an abundance of observations thanks to parallel experiments, current BO techniques have been limited to merely a few thousand observations. In this paper, we propose ensemble Bayesian optimization (EBO) to address three current challenges in BO simultaneously: (1) large-scale observations; (2) high dimensional input spaces; and (3) selections of batch queries that balance quality and diversity. The key idea of EBO is to operate on an ensemble of additive Gaussian process models, each of which possesses a randomized strategy to divide and conquer. We show unprecedented, previously impossible results of scaling up BO to tens of thousands of observations within minutes of computation.

Incremental Truncated LSTD

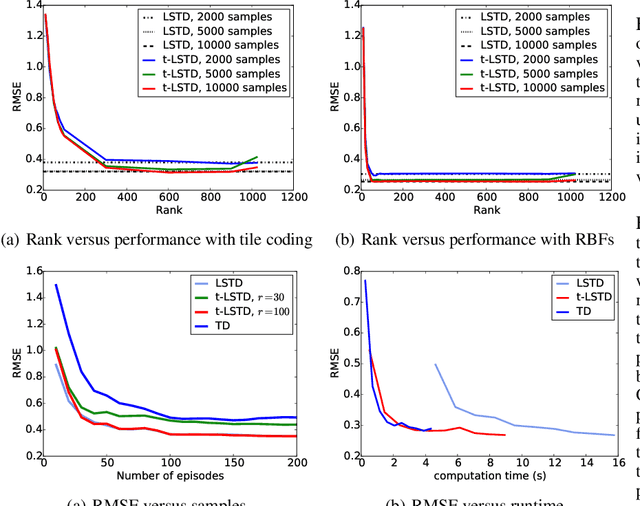
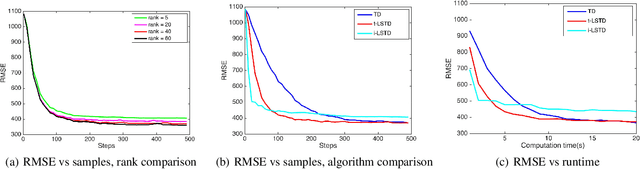
Balancing between computational efficiency and sample efficiency is an important goal in reinforcement learning. Temporal difference (TD) learning algorithms stochastically update the value function, with a linear time complexity in the number of features, whereas least-squares temporal difference (LSTD) algorithms are sample efficient but can be quadratic in the number of features. In this work, we develop an efficient incremental low-rank LSTD({\lambda}) algorithm that progresses towards the goal of better balancing computation and sample efficiency. The algorithm reduces the computation and storage complexity to the number of features times the chosen rank parameter while summarizing past samples efficiently to nearly obtain the sample complexity of LSTD. We derive a simulation bound on the solution given by truncated low-rank approximation, illustrating a bias- variance trade-off dependent on the choice of rank. We demonstrate that the algorithm effectively balances computational complexity and sample efficiency for policy evaluation in a benchmark task and a high-dimensional energy allocation domain.