ParalESN: Enabling parallel information processing in Reservoir Computing

Reservoir Computing (RC) has established itself as an efficient paradigm for temporal processing. However, its scalability remains severely constrained by (i) the necessity of processing temporal data sequentially and (ii) the prohibitive memory footprint of high-dimensional reservoirs. In this work, we revisit RC through the lens of structured operators and state space modeling to address these limitations, introducing Parallel Echo State Network (ParalESN). ParalESN enables the construction of high-dimensional and efficient reservoirs based on diagonal linear recurrence in the complex space, enabling parallel processing of temporal data. We provide a theoretical analysis demonstrating that ParalESN preserves the Echo State Property and the universality guarantees of traditional Echo State Networks while admitting an equivalent representation of arbitrary linear reservoirs in the complex diagonal form. Empirically, ParalESN matches the predictive accuracy of traditional RC on time series benchmarks, while delivering substantial computational savings. On 1-D pixel-level classification tasks, ParalESN achieves competitive accuracy with fully trainable neural networks while reducing computational costs and energy consumption by orders of magnitude. Overall, ParalESN offers a promising, scalable, and principled pathway for integrating RC within the deep learning landscape.

Deep Residual Echo State Networks: exploring residual orthogonal connections in untrained Recurrent Neural Networks

Echo State Networks (ESNs) are a particular type of untrained Recurrent Neural Networks (RNNs) within the Reservoir Computing (RC) framework, popular for their fast and efficient learning. However, traditional ESNs often struggle with long-term information processing. In this paper, we introduce a novel class of deep untrained RNNs based on temporal residual connections, called Deep Residual Echo State Networks (DeepResESNs). We show that leveraging a hierarchy of untrained residual recurrent layers significantly boosts memory capacity and long-term temporal modeling. For the temporal residual connections, we consider different orthogonal configurations, including randomly generated and fixed-structure configurations, and we study their effect on network dynamics. A thorough mathematical analysis outlines necessary and sufficient conditions to ensure stable dynamics within DeepResESN. Our experiments on a variety of time series tasks showcase the advantages of the proposed approach over traditional shallow and deep RC.

Residual Reservoir Memory Networks

We introduce a novel class of untrained Recurrent Neural Networks (RNNs) within the Reservoir Computing (RC) paradigm, called Residual Reservoir Memory Networks (ResRMNs). ResRMN combines a linear memory reservoir with a non-linear reservoir, where the latter is based on residual orthogonal connections along the temporal dimension for enhanced long-term propagation of the input. The resulting reservoir state dynamics are studied through the lens of linear stability analysis, and we investigate diverse configurations for the temporal residual connections. The proposed approach is empirically assessed on time-series and pixel-level 1-D classification tasks. Our experimental results highlight the advantages of the proposed approach over other conventional RC models.

Mixture of Raytraced Experts

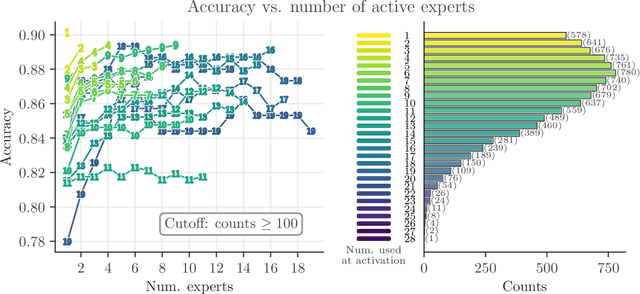
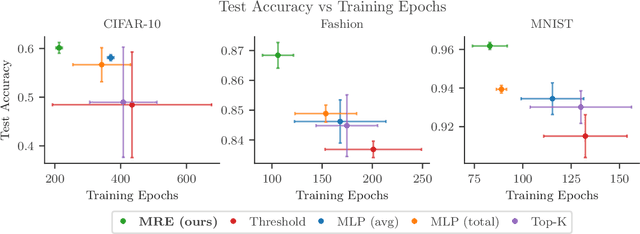
We introduce a Mixture of Raytraced Experts, a stacked Mixture of Experts (MoE) architecture which can dynamically select sequences of experts, producing computational graphs of variable width and depth. Existing MoE architectures generally require a fixed amount of computation for a given sample. Our approach, in contrast, yields predictions with increasing accuracy as the computation cycles through the experts' sequence. We train our model by iteratively sampling from a set of candidate experts, unfolding the sequence akin to how Recurrent Neural Networks are trained. Our method does not require load-balancing mechanisms, and preliminary experiments show a reduction in training epochs of 10\% to 40\% with a comparable/higher accuracy. These results point to new research directions in the field of MoEs, allowing the design of potentially faster and more expressive models. The code is available at https://github.com/nutig/RayTracing

Message-Passing State-Space Models: Improving Graph Learning with Modern Sequence Modeling

The recent success of State-Space Models (SSMs) in sequence modeling has motivated their adaptation to graph learning, giving rise to Graph State-Space Models (GSSMs). However, existing GSSMs operate by applying SSM modules to sequences extracted from graphs, often compromising core properties such as permutation equivariance, message-passing compatibility, and computational efficiency. In this paper, we introduce a new perspective by embedding the key principles of modern SSM computation directly into the Message-Passing Neural Network framework, resulting in a unified methodology for both static and temporal graphs. Our approach, MP-SSM, enables efficient, permutation-equivariant, and long-range information propagation while preserving the architectural simplicity of message passing. Crucially, MP-SSM enables an exact sensitivity analysis, which we use to theoretically characterize information flow and evaluate issues like vanishing gradients and over-squashing in the deep regime. Furthermore, our design choices allow for a highly optimized parallel implementation akin to modern SSMs. We validate MP-SSM across a wide range of tasks, including node classification, graph property prediction, long-range benchmarks, and spatiotemporal forecasting, demonstrating both its versatility and strong empirical performance.

Ray-Tracing for Conditionally Activated Neural Networks

In this paper, we introduce a novel architecture for conditionally activated neural networks combining a hierarchical construction of multiple Mixture of Experts (MoEs) layers with a sampling mechanism that progressively converges to an optimized configuration of expert activation. This methodology enables the dynamic unfolding of the network's architecture, facilitating efficient path-specific training. Experimental results demonstrate that this approach achieves competitive accuracy compared to conventional baselines while significantly reducing the parameter count required for inference. Notably, this parameter reduction correlates with the complexity of the input patterns, a property naturally emerging from the network's operational dynamics without necessitating explicit auxiliary penalty functions.

Long Range Propagation on Continuous-Time Dynamic Graphs

Learning Continuous-Time Dynamic Graphs (C-TDGs) requires accurately modeling spatio-temporal information on streams of irregularly sampled events. While many methods have been proposed recently, we find that most message passing-, recurrent- or self-attention-based methods perform poorly on long-range tasks. These tasks require correlating information that occurred "far" away from the current event, either spatially (higher-order node information) or along the time dimension (events occurred in the past). To address long-range dependencies, we introduce Continuous-Time Graph Anti-Symmetric Network (CTAN). Grounded within the ordinary differential equations framework, our method is designed for efficient propagation of information. In this paper, we show how CTAN's (i) long-range modeling capabilities are substantiated by theoretical findings and how (ii) its empirical performance on synthetic long-range benchmarks and real-world benchmarks is superior to other methods. Our results motivate CTAN's ability to propagate long-range information in C-TDGs as well as the inclusion of long-range tasks as part of temporal graph models evaluation.

Injecting Hamiltonian Architectural Bias into Deep Graph Networks for Long-Range Propagation

The dynamics of information diffusion within graphs is a critical open issue that heavily influences graph representation learning, especially when considering long-range propagation. This calls for principled approaches that control and regulate the degree of propagation and dissipation of information throughout the neural flow. Motivated by this, we introduce (port-)Hamiltonian Deep Graph Networks, a novel framework that models neural information flow in graphs by building on the laws of conservation of Hamiltonian dynamical systems. We reconcile under a single theoretical and practical framework both non-dissipative long-range propagation and non-conservative behaviors, introducing tools from mechanical systems to gauge the equilibrium between the two components. Our approach can be applied to general message-passing architectures, and it provides theoretical guarantees on information conservation in time. Empirical results prove the effectiveness of our port-Hamiltonian scheme in pushing simple graph convolutional architectures to state-of-the-art performance in long-range benchmarks.

Tackling Graph Oversquashing by Global and Local Non-Dissipativity

A common problem in Message-Passing Neural Networks is oversquashing -- the limited ability to facilitate effective information flow between distant nodes. Oversquashing is attributed to the exponential decay in information transmission as node distances increase. This paper introduces a novel perspective to address oversquashing, leveraging properties of global and local non-dissipativity, that enable the maintenance of a constant information flow rate. Namely, we present SWAN, a uniquely parameterized model GNN with antisymmetry both in space and weight domains, as a means to obtain non-dissipativity. Our theoretical analysis asserts that by achieving these properties, SWAN offers an enhanced ability to transmit information over extended distances. Empirical evaluations on synthetic and real-world benchmarks that emphasize long-range interactions validate the theoretical understanding of SWAN, and its ability to mitigate oversquashing.

Awareness in robotics: An early perspective from the viewpoint of the EIC Pathfinder Challenge "Awareness Inside''

Consciousness has been historically a heavily debated topic in engineering, science, and philosophy. On the contrary, awareness had less success in raising the interest of scholars in the past. However, things are changing as more and more researchers are getting interested in answering questions concerning what awareness is and how it can be artificially generated. The landscape is rapidly evolving, with multiple voices and interpretations of the concept being conceived and techniques being developed. The goal of this paper is to summarize and discuss the ones among these voices connected with projects funded by the EIC Pathfinder Challenge called ``Awareness Inside'', a nonrecurring call for proposals within Horizon Europe designed specifically for fostering research on natural and synthetic awareness. In this perspective, we dedicate special attention to challenges and promises of applying synthetic awareness in robotics, as the development of mature techniques in this new field is expected to have a special impact on generating more capable and trustworthy embodied systems.