Combining Optimal Control and Learning for Visual Navigation in Novel Environments

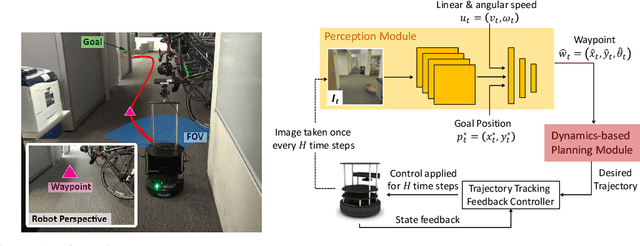
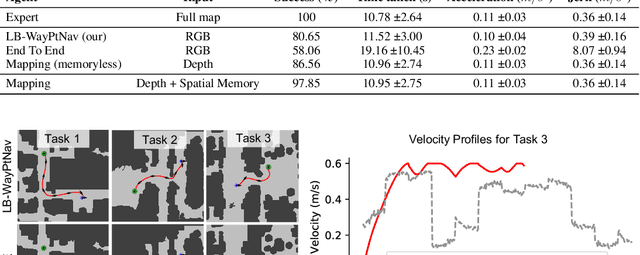
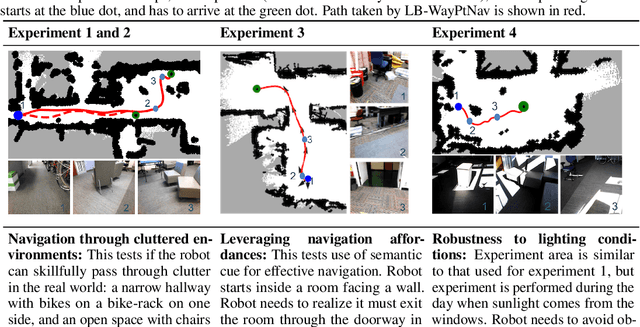
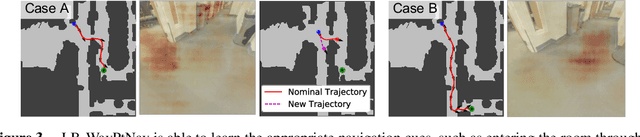
Model-based control is a popular paradigm for robot navigation because it can leverage a known dynamics model to efficiently plan robust robot trajectories. However, it is challenging to use model-based methods in settings where the environment is a priori unknown and can only be observed partially through on-board sensors on the robot. In this work, we address this short-coming by coupling model-based control with learning-based perception. The learning-based perception module produces a series of waypoints that guide the robot to the goal via a collision-free path. These waypoints are used by a model-based planner to generate a smooth and dynamically feasible trajectory that is executed on the physical system using feedback control. Our experiments in simulated real-world cluttered environments and on an actual ground vehicle demonstrate that the proposed approach can reach goal locations more reliably and efficiently in novel, previously-unknown environments as compared to a purely end-to-end learning-based alternative. Our approach is successfully able to exhibit goal-driven behavior without relying on detailed explicit 3D maps of the environment, works well with low frame rates, and generalizes well from simulation to the real world. Videos describing our approach and experiments are available on the project website.

Regression-based Inverter Control for Decentralized Optimal Power Flow and Voltage Regulation

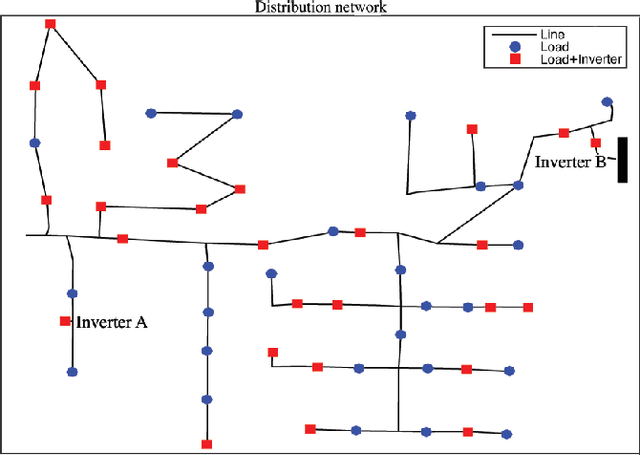
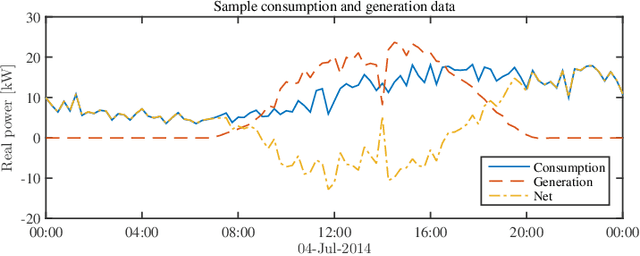
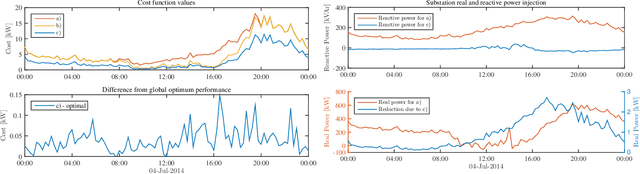
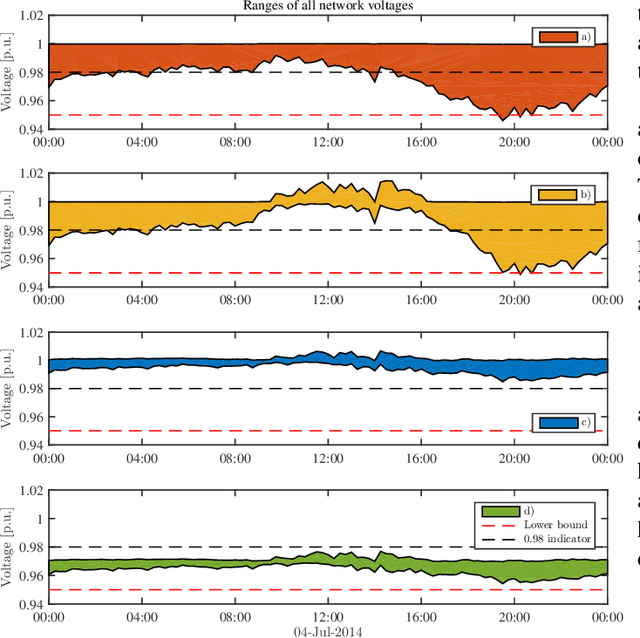
Electronic power inverters are capable of quickly delivering reactive power to maintain customer voltages within operating tolerances and to reduce system losses in distribution grids. This paper proposes a systematic and data-driven approach to determine reactive power inverter output as a function of local measurements in a manner that obtains near optimal results. First, we use a network model and historic load and generation data and do optimal power flow to compute globally optimal reactive power injections for all controllable inverters in the network. Subsequently, we use regression to find a function for each inverter that maps its local historical data to an approximation of its optimal reactive power injection. The resulting functions then serve as decentralized controllers in the participating inverters to predict the optimal injection based on a new local measurements. The method achieves near-optimal results when performing voltage- and capacity-constrained loss minimization and voltage flattening, and allows for an efficient volt-VAR optimization (VVO) scheme in which legacy control equipment collaborates with existing inverters to facilitate safe operation of distribution networks with higher levels of distributed generation.

A Successive-Elimination Approach to Adaptive Robotic Sensing

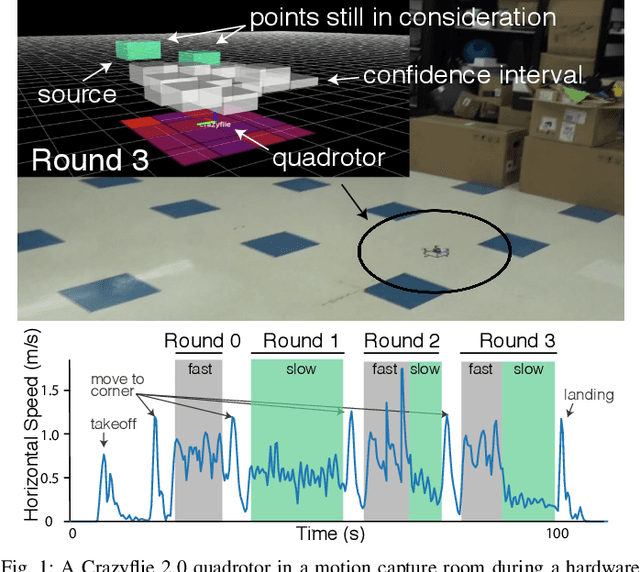
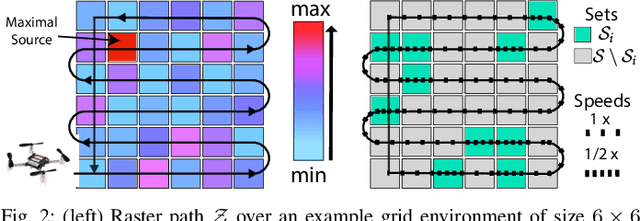
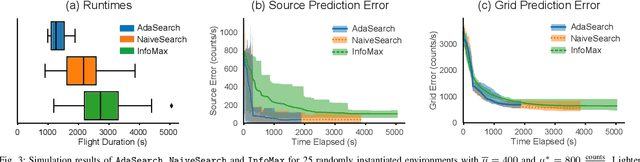
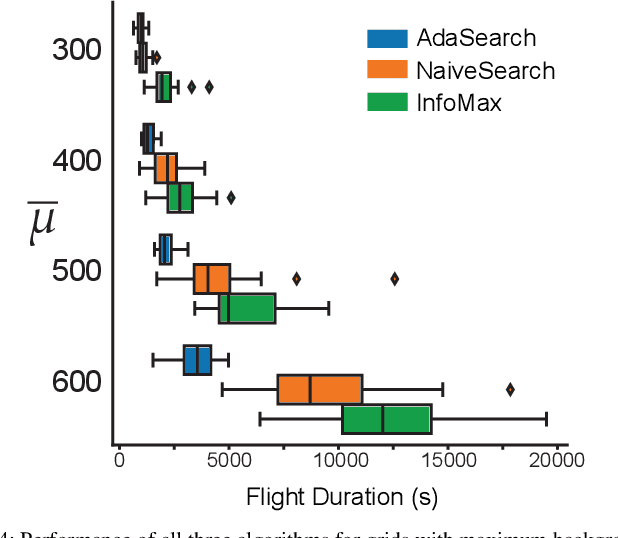
We study the adaptive sensing problem for the multiple source seeking problem, where a mobile robot must identify the strongest emitters in an environment with background emissions. Background signals may be highly heterogeneous, and can mislead algorithms which are based on receding horizon control, greedy heuristics, or smooth background priors. We propose AdaSearch, a general algorithm for adaptive sensing. AdaSearch combines global trajectory planning with principled confidence intervals in order to concentrate measurements in promising regions while still guaranteeing sufficient coverage of the entire area. Theoretical analysis shows that AdaSearch significantly outperforms a uniform sampling strategy when the distribution of background signals is highly variable. Simulation studies demonstrate that when applied to the problem of radioactive source-seeking, AdaSearch outperforms both uniform sampling and a receding time horizon information-maximization approach based on the current literature. We corroborate these findings with a hardware demonstration, using a small quadrotor helicopter in a motion-capture arena.

The Parallelization of Riccati Recursion

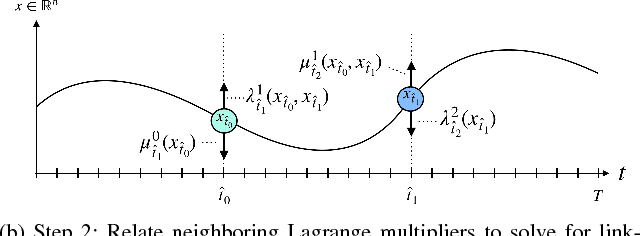
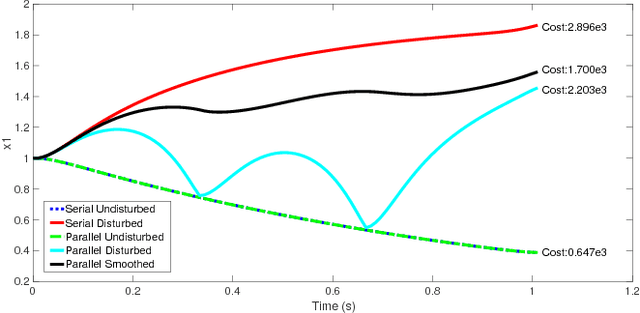
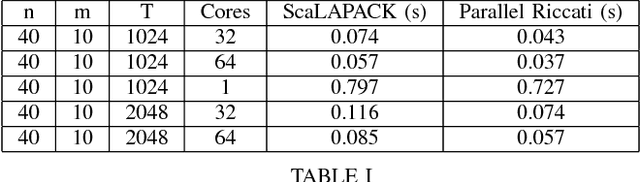
A method is presented for parallelizing the computation of solutions to discrete-time, linear-quadratic, finite-horizon optimal control problems, which we will refer to as LQR problems. This class of problem arises frequently in robotic trajectory optimization. For very complicated robots, the size of these resulting problems can be large enough that computing the solution is prohibitively slow when using a single processor. Fortunately, approaches to solving these type of problems based on numerical solutions to the KKT conditions of optimality offer a parallel solution method and can leverage multiple processors to compute solutions faster. However, these methods do not produce the useful feedback control policies that are generated as a by-product of the dynamic-programming solution method known as Riccati recursion. In this paper we derive a method which is able to parallelize the computation of Riccati recursion, allowing for super-fast solutions to the LQR problem while still generating feedback control policies. We demonstrate empirically that our method is faster than existing parallel methods.

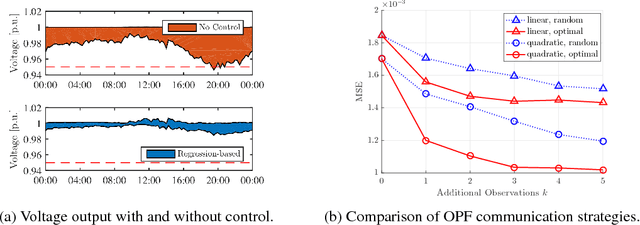
Data-Driven Decentralized Optimal Power Flow

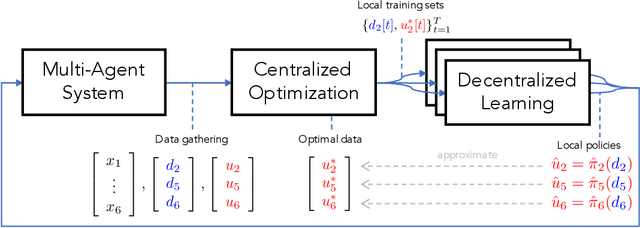
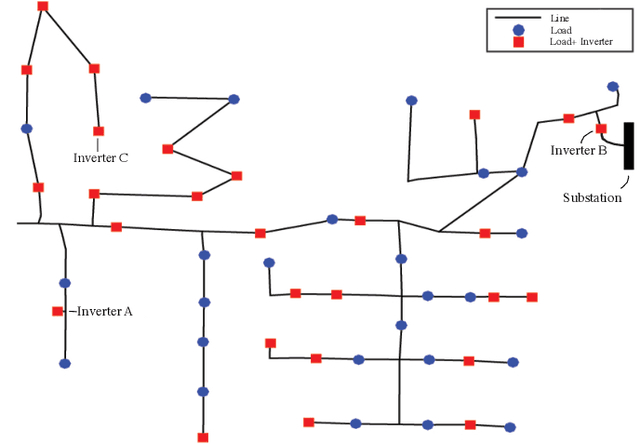
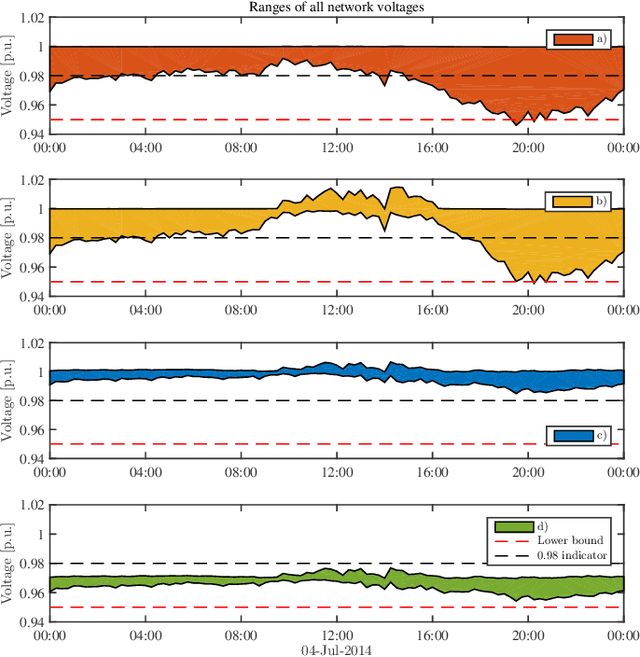
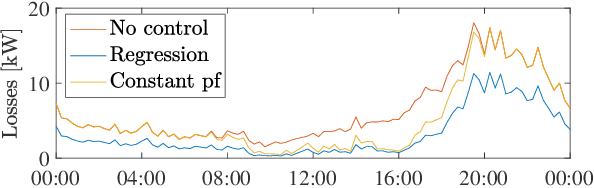
The implementation of optimal power flow (OPF) methods to perform voltage and power flow regulation in electric networks is generally believed to require communication. We consider distribution systems with multiple controllable Distributed Energy Resources (DERs) and present a data-driven approach to learn control policies for each DER to reconstruct and mimic the solution to a centralized OPF problem from solely locally available information. Collectively, all local controllers closely match the centralized OPF solution, providing near-optimal performance and satisfaction of system constraints. A rate distortion framework facilitates the analysis of how well the resulting fully decentralized control policies are able to reconstruct the OPF solution. Our methodology provides a natural extension to decide what buses a DER should communicate with to improve the reconstruction of its individual policy. The method is applied on both single- and three-phase test feeder networks using data from real loads and distributed generators. It provides a framework for Distribution System Operators to efficiently plan and operate the contributions of DERs to active distribution networks.

On Identification of Distribution Grids

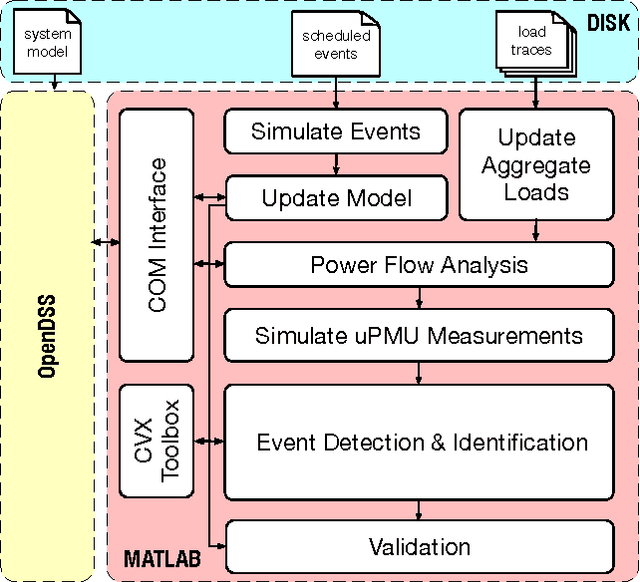
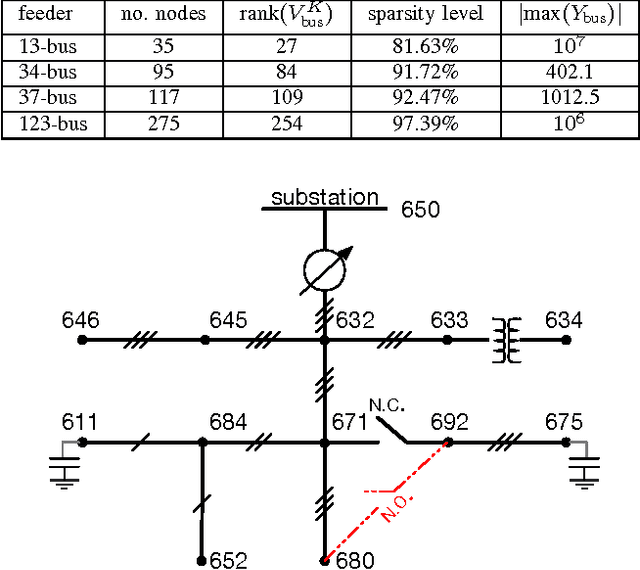
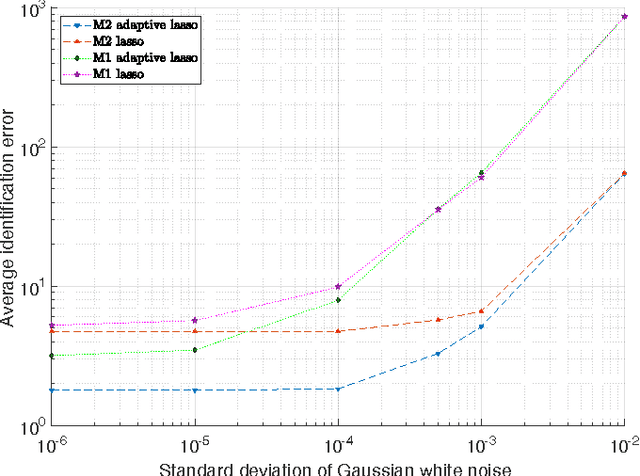
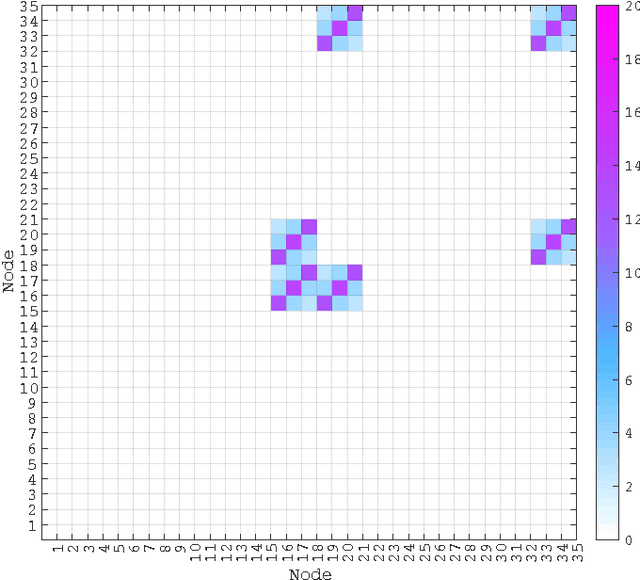
Large-scale integration of distributed energy resources into residential distribution feeders necessitates careful control of their operation through power flow analysis. While the knowledge of the distribution system model is crucial for this type of analysis, it is often unavailable or outdated. The recent introduction of synchrophasor technology in low-voltage distribution grids has created an unprecedented opportunity to learn this model from high-precision, time-synchronized measurements of voltage and current phasors at various locations. This paper focuses on joint estimation of model parameters (admittance values) and operational structure of a poly-phase distribution network from the available telemetry data via the lasso, a method for regression shrinkage and selection. We propose tractable convex programs capable of tackling the low rank structure of the distribution system and develop an online algorithm for early detection and localization of critical events that induce a change in the admittance matrix. The efficacy of these techniques is corroborated through power flow studies on four three-phase radial distribution systems serving real household demands.

A Sequential Approximation Framework for Coded Distributed Optimization

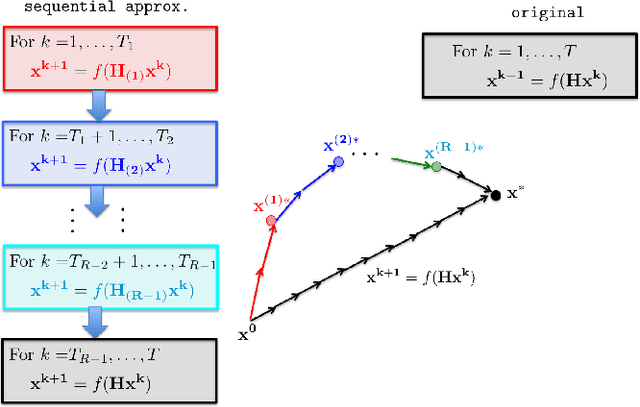
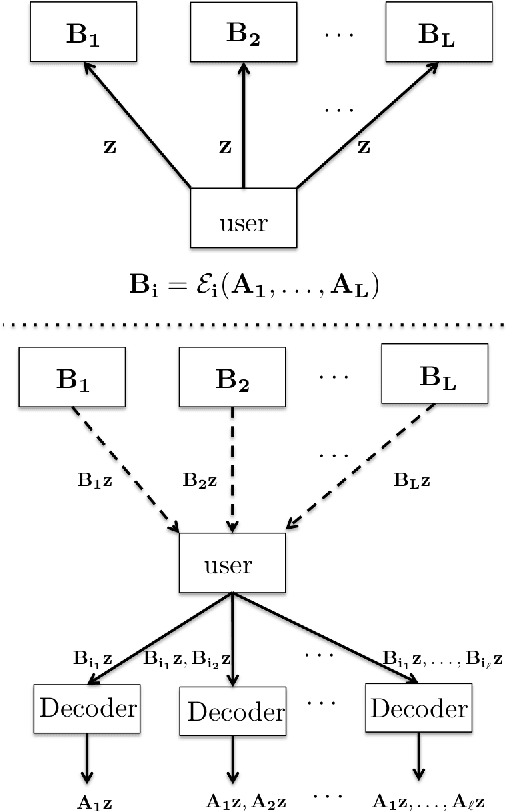
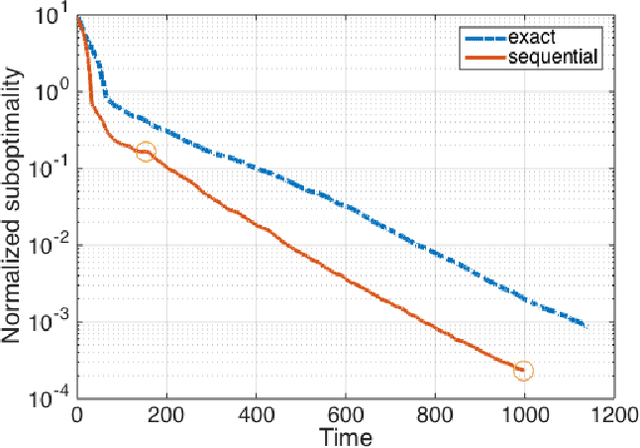
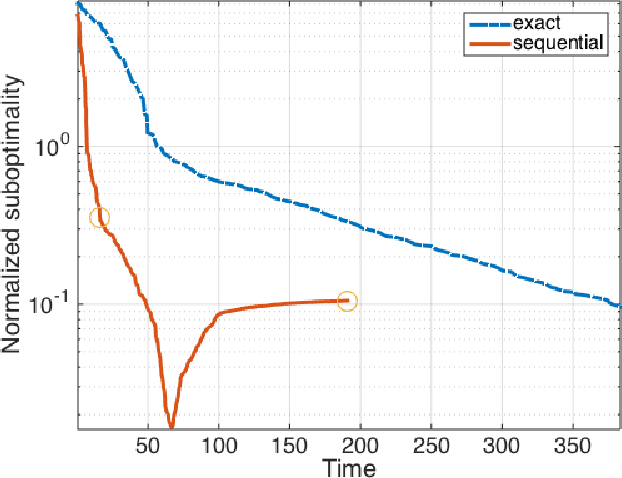
Building on the previous work of Lee et al. and Ferdinand et al. on coded computation, we propose a sequential approximation framework for solving optimization problems in a distributed manner. In a distributed computation system, latency caused by individual processors ("stragglers") usually causes a significant delay in the overall process. The proposed method is powered by a sequential computation scheme, which is designed specifically for systems with stragglers. This scheme has the desirable property that the user is guaranteed to receive useful (approximate) computation results whenever a processor finishes its subtask, even in the presence of uncertain latency. In this paper, we give a coding theorem for sequentially computing matrix-vector multiplications, and the optimality of this coding scheme is also established. As an application of the results, we demonstrate solving optimization problems using a sequential approximation approach, which accelerates the algorithm in a distributed system with stragglers.

MBMF: Model-Based Priors for Model-Free Reinforcement Learning

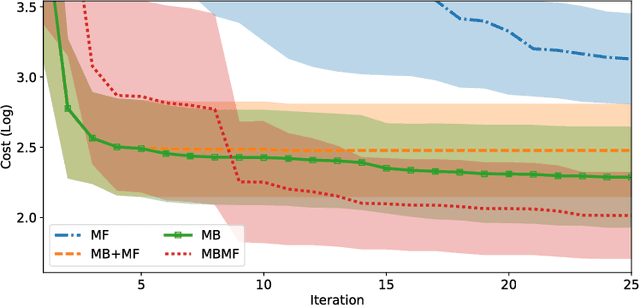
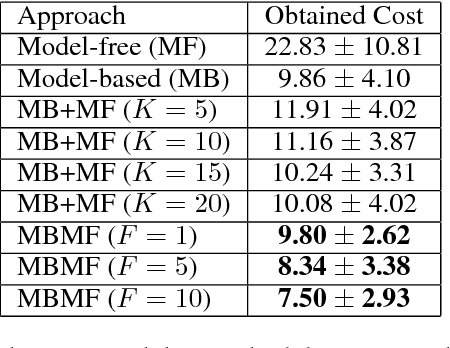
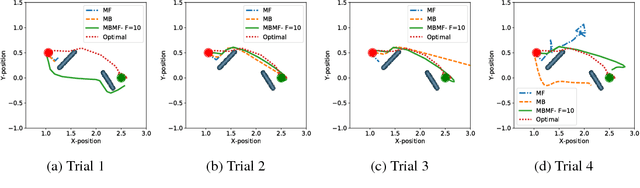
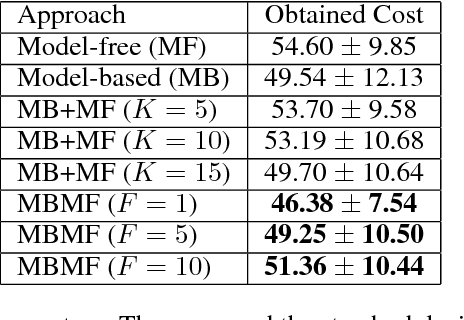
Reinforcement Learning is divided in two main paradigms: model-free and model-based. Each of these two paradigms has strengths and limitations, and has been successfully applied to real world domains that are appropriate to its corresponding strengths. In this paper, we present a new approach aimed at bridging the gap between these two paradigms. We aim to take the best of the two paradigms and combine them in an approach that is at the same time data-efficient and cost-savvy. We do so by learning a probabilistic dynamics model and leveraging it as a prior for the intertwined model-free optimization. As a result, our approach can exploit the generality and structure of the dynamics model, but is also capable of ignoring its inevitable inaccuracies, by directly incorporating the evidence provided by the direct observation of the cost. Preliminary results demonstrate that our approach outperforms purely model-based and model-free approaches, as well as the approach of simply switching from a model-based to a model-free setting.

Fully Decentralized Policies for Multi-Agent Systems: An Information Theoretic Approach

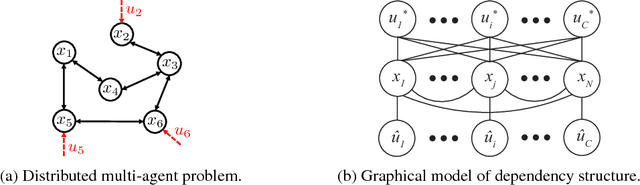
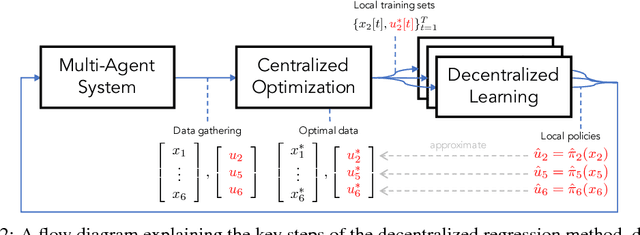
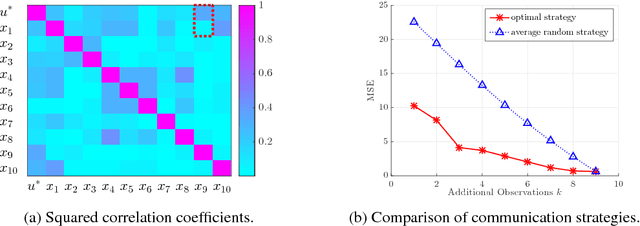
Learning cooperative policies for multi-agent systems is often challenged by partial observability and a lack of coordination. In some settings, the structure of a problem allows a distributed solution with limited communication. Here, we consider a scenario where no communication is available, and instead we learn local policies for all agents that collectively mimic the solution to a centralized multi-agent static optimization problem. Our main contribution is an information theoretic framework based on rate distortion theory which facilitates analysis of how well the resulting fully decentralized policies are able to reconstruct the optimal solution. Moreover, this framework provides a natural extension that addresses which nodes an agent should communicate with to improve the performance of its individual policy.

Recursive Regression with Neural Networks: Approximating the HJI PDE Solution

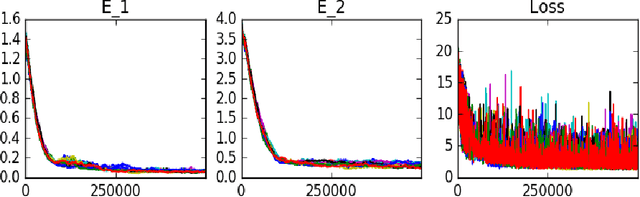
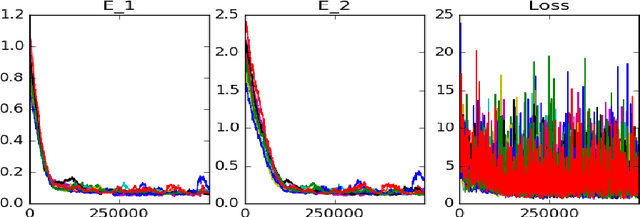
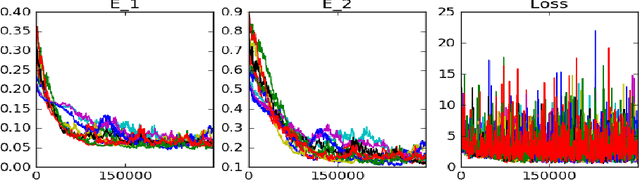
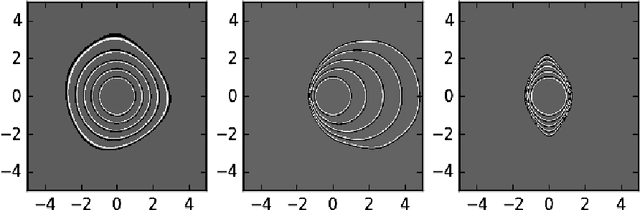
The majority of methods used to compute approximations to the Hamilton-Jacobi-Isaacs partial differential equation (HJI PDE) rely on the discretization of the state space to perform dynamic programming updates. This type of approach is known to suffer from the curse of dimensionality due to the exponential growth in grid points with the state dimension. In this work we present an approximate dynamic programming algorithm that computes an approximation of the solution of the HJI PDE by alternating between solving a regression problem and solving a minimax problem using a feedforward neural network as the function approximator. We find that this method requires less memory to run and to store the approximation than traditional gridding methods, and we test it on a few systems of two, three and six dimensions.