Chenlu Ye
Reinforce-Ada: An Adaptive Sampling Framework for Reinforce-Style LLM Training
Oct 06, 2025Abstract:Reinforcement learning applied to large language models (LLMs) for reasoning tasks is often bottlenecked by unstable gradient estimates due to fixed and uniform sampling of responses across prompts. Prior work such as GVM-RAFT addresses this by dynamically allocating inference budget per prompt to minimize stochastic gradient variance under a budget constraint. Inspired by this insight, we propose Reinforce-Ada, an adaptive sampling framework for online RL post-training of LLMs that continuously reallocates sampling effort to the prompts with the greatest uncertainty or learning potential. Unlike conventional two-stage allocation methods, Reinforce-Ada interleaves estimation and sampling in an online successive elimination process, and automatically stops sampling for a prompt once sufficient signal is collected. To stabilize updates, we form fixed-size groups with enforced reward diversity and compute advantage baselines using global statistics aggregated over the adaptive sampling phase. Empirical results across multiple model architectures and reasoning benchmarks show that Reinforce-Ada accelerates convergence and improves final performance compared to GRPO, especially when using the balanced sampling variant. Our work highlights the central role of variance-aware, adaptive data curation in enabling efficient and reliable reinforcement learning for reasoning-capable LLMs. Code is available at https://github.com/RLHFlow/Reinforce-Ada.
Beyond Correctness: Harmonizing Process and Outcome Rewards through RL Training
Sep 03, 2025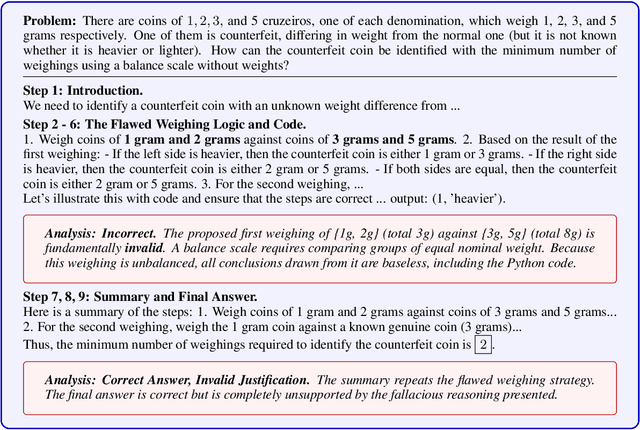

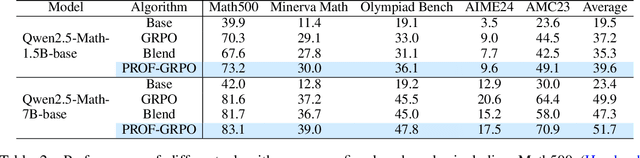
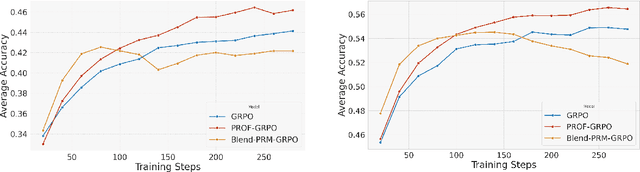
Abstract:Reinforcement learning with verifiable rewards (RLVR) has emerged to be a predominant paradigm for mathematical reasoning tasks, offering stable improvements in reasoning ability. However, Outcome Reward Models (ORMs) in RLVR are too coarse-grained to distinguish flawed reasoning within correct answers or valid reasoning within incorrect answers. This lack of granularity introduces noisy and misleading gradients significantly and hinders further progress in reasoning process quality. While Process Reward Models (PRMs) offer fine-grained guidance for intermediate steps, they frequently suffer from inaccuracies and are susceptible to reward hacking. To resolve this dilemma, we introduce PRocess cOnsistency Filter (PROF), an effective data process curation method that harmonizes noisy, fine-grained process rewards with accurate, coarse-grained outcome rewards. Rather than naively blending PRM and ORM in the objective function (arXiv:archive/2506.18896), PROF leverages their complementary strengths through consistency-driven sample selection. Our approach retains correct responses with higher averaged process values and incorrect responses with lower averaged process values, while maintaining positive/negative training sample balance. Extensive experiments demonstrate that our method not only consistently improves the final accuracy over $4\%$ compared to the blending approaches, but also strengthens the quality of intermediate reasoning steps. Codes and training recipes are available at https://github.com/Chenluye99/PROF.
Daunce: Data Attribution through Uncertainty Estimation
May 29, 2025Abstract:Training data attribution (TDA) methods aim to identify which training examples influence a model's predictions on specific test data most. By quantifying these influences, TDA supports critical applications such as data debugging, curation, and valuation. Gradient-based TDA methods rely on gradients and second-order information, limiting their applicability at scale. While recent random projection-based methods improve scalability, they often suffer from degraded attribution accuracy. Motivated by connections between uncertainty and influence functions, we introduce Daunce - a simple yet effective data attribution approach through uncertainty estimation. Our method operates by fine-tuning a collection of perturbed models and computing the covariance of per-example losses across these models as the attribution score. Daunce is scalable to large language models (LLMs) and achieves more accurate attribution compared to existing TDA methods. We validate Daunce on tasks ranging from vision tasks to LLM fine-tuning, and further demonstrate its compatibility with black-box model access. Applied to OpenAI's GPT models, our method achieves, to our knowledge, the first instance of data attribution on proprietary LLMs.
Self-rewarding correction for mathematical reasoning
Feb 26, 2025Abstract:We study self-rewarding reasoning large language models (LLMs), which can simultaneously generate step-by-step reasoning and evaluate the correctness of their outputs during the inference time-without external feedback. This integrated approach allows a single model to independently guide its reasoning process, offering computational advantages for model deployment. We particularly focus on the representative task of self-correction, where models autonomously detect errors in their responses, revise outputs, and decide when to terminate iterative refinement loops. To enable this, we propose a two-staged algorithmic framework for constructing self-rewarding reasoning models using only self-generated data. In the first stage, we employ sequential rejection sampling to synthesize long chain-of-thought trajectories that incorporate both self-rewarding and self-correction mechanisms. Fine-tuning models on these curated data allows them to learn the patterns of self-rewarding and self-correction. In the second stage, we further enhance the models' ability to assess response accuracy and refine outputs through reinforcement learning with rule-based signals. Experiments with Llama-3 and Qwen-2.5 demonstrate that our approach surpasses intrinsic self-correction capabilities and achieves performance comparable to systems that rely on external reward models.
Logarithmic Regret for Online KL-Regularized Reinforcement Learning
Feb 11, 2025
Abstract:Recent advances in Reinforcement Learning from Human Feedback (RLHF) have shown that KL-regularization plays a pivotal role in improving the efficiency of RL fine-tuning for large language models (LLMs). Despite its empirical advantage, the theoretical difference between KL-regularized RL and standard RL remains largely under-explored. While there is a recent line of work on the theoretical analysis of KL-regularized objective in decision making \citep{xiong2024iterative, xie2024exploratory,zhao2024sharp}, these analyses either reduce to the traditional RL setting or rely on strong coverage assumptions. In this paper, we propose an optimism-based KL-regularized online contextual bandit algorithm, and provide a novel analysis of its regret. By carefully leveraging the benign optimization landscape induced by the KL-regularization and the optimistic reward estimation, our algorithm achieves an $\mathcal{O}\big(\eta\log (N_{\mathcal R} T)\cdot d_{\mathcal R}\big)$ logarithmic regret bound, where $\eta, N_{\mathcal R},T,d_{\mathcal R}$ denote the KL-regularization parameter, the cardinality of the reward function class, number of rounds, and the complexity of the reward function class. Furthermore, we extend our algorithm and analysis to reinforcement learning by developing a novel decomposition over transition steps and also obtain a similar logarithmic regret bound.
Catoni Contextual Bandits are Robust to Heavy-tailed Rewards
Feb 04, 2025Abstract:Typical contextual bandit algorithms assume that the rewards at each round lie in some fixed range $[0, R]$, and their regret scales polynomially with this reward range $R$. However, many practical scenarios naturally involve heavy-tailed rewards or rewards where the worst-case range can be substantially larger than the variance. In this paper, we develop an algorithmic approach building on Catoni's estimator from robust statistics, and apply it to contextual bandits with general function approximation. When the variance of the reward at each round is known, we use a variance-weighted regression approach and establish a regret bound that depends only on the cumulative reward variance and logarithmically on the reward range $R$ as well as the number of rounds $T$. For the unknown-variance case, we further propose a careful peeling-based algorithm and remove the need for cumbersome variance estimation. With additional dependence on the fourth moment, our algorithm also enjoys a variance-based bound with logarithmic reward-range dependence. Moreover, we demonstrate the optimality of the leading-order term in our regret bound through a matching lower bound.
Sharp Analysis for KL-Regularized Contextual Bandits and RLHF
Nov 07, 2024

Abstract:Reverse-Kullback-Leibler (KL) regularization has emerged to be a predominant technique used to enhance policy optimization in reinforcement learning (RL) and reinforcement learning from human feedback (RLHF), which forces the learned policy to stay close to a reference policy. While the effectiveness and necessity of KL-regularization have been empirically demonstrated in various practical scenarios, current theoretical analysis of KL-regularized RLHF still obtains the same $\mathcal{O}(1 / \epsilon^2)$ sample complexity as problems without KL-regularization. To understand the fundamental distinction between policy learning objectives with KL-regularization and ones without KL-regularization, we are the first to theoretically demonstrate the power of KL-regularization by providing a sharp analysis for KL-regularized contextual bandits and RLHF, revealing an $\mathcal{O}(1 / \epsilon)$ sample complexity when $\epsilon$ is sufficiently small. We further explore the role of data coverage in contextual bandits and RLHF. While the coverage assumption is commonly employed in offline RLHF to link the samples from the reference policy to the optimal policy, often at the cost of a multiplicative dependence on the coverage coefficient, its impact on the sample complexity of online RLHF remains unclear. Previous theoretical analyses of online RLHF typically require explicit exploration and additional structural assumptions on the reward function class. In contrast, we show that with sufficient coverage from the reference policy, a simple two-stage mixed sampling strategy can achieve a sample complexity with only an additive dependence on the coverage coefficient. Our results provide a comprehensive understanding of the roles of KL-regularization and data coverage in RLHF, shedding light on the design of more efficient RLHF algorithms.
Towards Robust Model-Based Reinforcement Learning Against Adversarial Corruption
Feb 15, 2024Abstract:This study tackles the challenges of adversarial corruption in model-based reinforcement learning (RL), where the transition dynamics can be corrupted by an adversary. Existing studies on corruption-robust RL mostly focus on the setting of model-free RL, where robust least-square regression is often employed for value function estimation. However, these techniques cannot be directly applied to model-based RL. In this paper, we focus on model-based RL and take the maximum likelihood estimation (MLE) approach to learn transition model. Our work encompasses both online and offline settings. In the online setting, we introduce an algorithm called corruption-robust optimistic MLE (CR-OMLE), which leverages total-variation (TV)-based information ratios as uncertainty weights for MLE. We prove that CR-OMLE achieves a regret of $\tilde{\mathcal{O}}(\sqrt{T} + C)$, where $C$ denotes the cumulative corruption level after $T$ episodes. We also prove a lower bound to show that the additive dependence on $C$ is optimal. We extend our weighting technique to the offline setting, and propose an algorithm named corruption-robust pessimistic MLE (CR-PMLE). Under a uniform coverage condition, CR-PMLE exhibits suboptimality worsened by $\mathcal{O}(C/n)$, nearly matching the lower bound. To the best of our knowledge, this is the first work on corruption-robust model-based RL algorithms with provable guarantees.
A Theoretical Analysis of Nash Learning from Human Feedback under General KL-Regularized Preference
Feb 11, 2024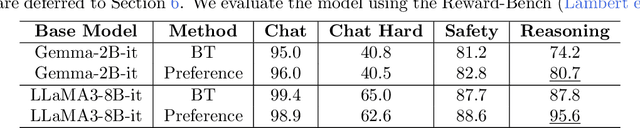
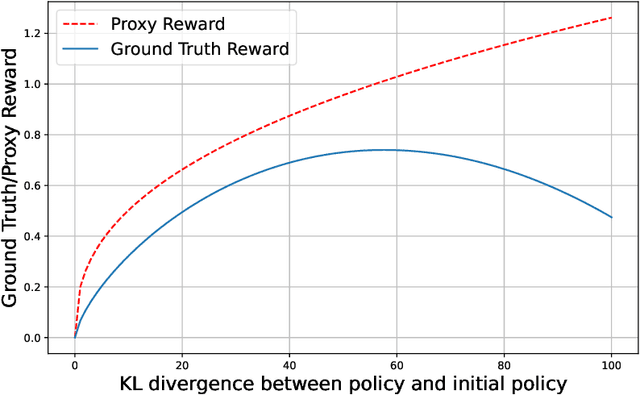

Abstract:Reinforcement Learning from Human Feedback (RLHF) learns from the preference signal provided by a probabilistic preference model, which takes a prompt and two responses as input, and produces a score indicating the preference of one response against another. So far, the most popular RLHF paradigm is reward-based, which starts with an initial step of reward modeling, and the constructed reward is then used to provide a reward signal for the subsequent reward optimization stage. However, the existence of a reward function is a strong assumption and the reward-based RLHF is limited in expressivity and cannot capture the real-world complicated human preference. In this work, we provide theoretical insights for a recently proposed learning paradigm, Nash learning from human feedback (NLHF), which considered a general preference model and formulated the alignment process as a game between two competitive LLMs. The learning objective is to find a policy that consistently generates responses preferred over any competing policy while staying close to the initial model. The objective is defined as the Nash equilibrium (NE) of the KL-regularized preference model. We aim to make the first attempt to study the theoretical learnability of the KL-regularized NLHF by considering both offline and online settings. For the offline learning from a pre-collected dataset, we propose algorithms that are efficient under suitable coverage conditions of the dataset. For batch online learning from iterative interactions with a preference oracle, our proposed algorithm enjoys a finite sample guarantee under the structural condition of the underlying preference model. Our results connect the new NLHF paradigm with traditional RL theory, and validate the potential of reward-model-free learning under general preference.
Gibbs Sampling from Human Feedback: A Provable KL- constrained Framework for RLHF
Dec 18, 2023



Abstract:This paper studies the theoretical framework of the alignment process of generative models with Reinforcement Learning from Human Feedback (RLHF). We consider a standard mathematical formulation, the reverse-KL regularized contextual bandit for RLHF. Despite its widespread practical application, a rigorous theoretical analysis of this formulation remains open. We investigate its theoretical properties both in offline and online settings and propose efficient algorithms with finite-sample theoretical guarantees. Our work bridges the gap between theory and practice by linking our theoretical insights with existing practical alignment algorithms such as Direct Preference Optimization (DPO) and Rejection Sampling Optimization (RSO). Furthermore, these findings and connections also offer both theoretical and practical communities new tools and insights for future algorithmic design of alignment algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge