Cameron Musco
Random Fourier Features for Kernel Ridge Regression: Approximation Bounds and Statistical Guarantees
May 21, 2018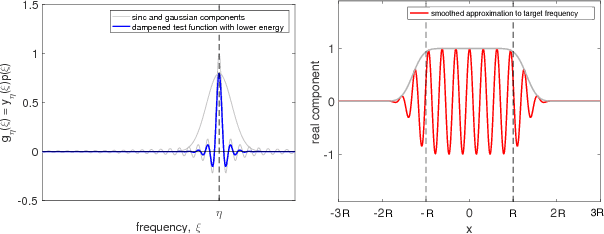
Abstract:Random Fourier features is one of the most popular techniques for scaling up kernel methods, such as kernel ridge regression. However, despite impressive empirical results, the statistical properties of random Fourier features are still not well understood. In this paper we take steps toward filling this gap. Specifically, we approach random Fourier features from a spectral matrix approximation point of view, give tight bounds on the number of Fourier features required to achieve a spectral approximation, and show how spectral matrix approximation bounds imply statistical guarantees for kernel ridge regression. Qualitatively, our results are twofold: on the one hand, we show that random Fourier feature approximation can provably speed up kernel ridge regression under reasonable assumptions. At the same time, we show that the method is suboptimal, and sampling from a modified distribution in Fourier space, given by the leverage function of the kernel, yields provably better performance. We study this optimal sampling distribution for the Gaussian kernel, achieving a nearly complete characterization for the case of low-dimensional bounded datasets. Based on this characterization, we propose an efficient sampling scheme with guarantees superior to random Fourier features in this regime.
Learning Networks from Random Walk-Based Node Similarities
Jan 23, 2018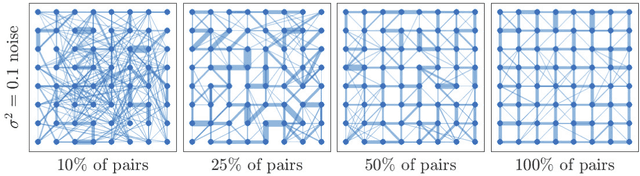
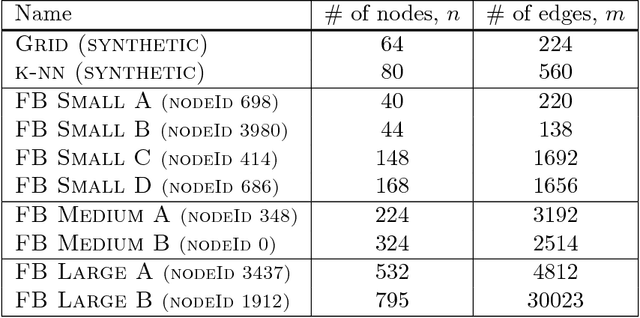
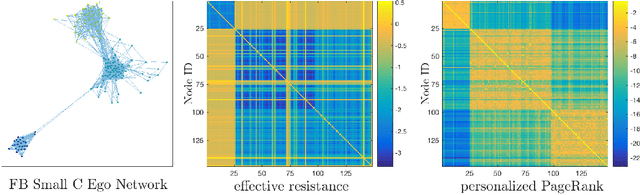
Abstract:Digital presence in the world of online social media entails significant privacy risks. In this work we consider a privacy threat to a social network in which an attacker has access to a subset of random walk-based node similarities, such as effective resistances (i.e., commute times) or personalized PageRank scores. Using these similarities, the attacker's goal is to infer as much information as possible about the underlying network, including any remaining unknown pairwise node similarities and edges. For the effective resistance metric, we show that with just a small subset of measurements, the attacker can learn a large fraction of edges in a social network, even when the measurements are noisy. We also show that it is possible to learn a graph which accurately matches the underlying network on all other effective resistances. This second observation is interesting from a data mining perspective, since it can be expensive to accurately compute all effective resistances. As an alternative, our graphs learned from just a subset of approximate effective resistances can be used as surrogates in a wide range of applications that use effective resistances to probe graph structure, including for graph clustering, node centrality evaluation, and anomaly detection. We obtain our results by formalizing the graph learning objective mathematically, using two optimization problems. One formulation is convex and can be solved provably in polynomial time. The other is not, but we solve it efficiently with projected gradient and coordinate descent. We demonstrate the effectiveness of these methods on a number of social networks obtained from Facebook. We also discuss how our methods can be generalized to other random walk-based similarities, such as personalized PageRank. Our code is available at https://github.com/cnmusco/graph-similarity-learning.
Minimizing Polarization and Disagreement in Social Networks
Dec 28, 2017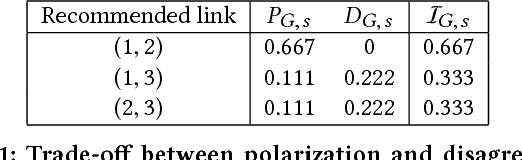
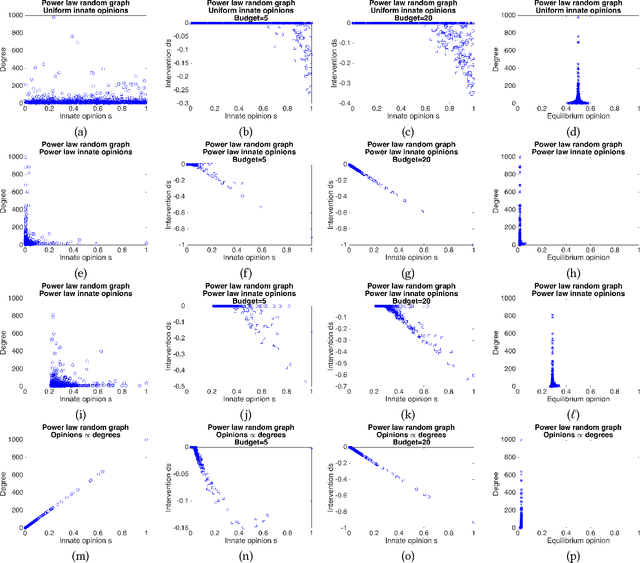
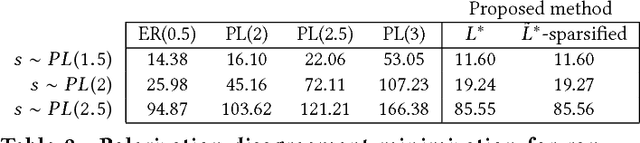
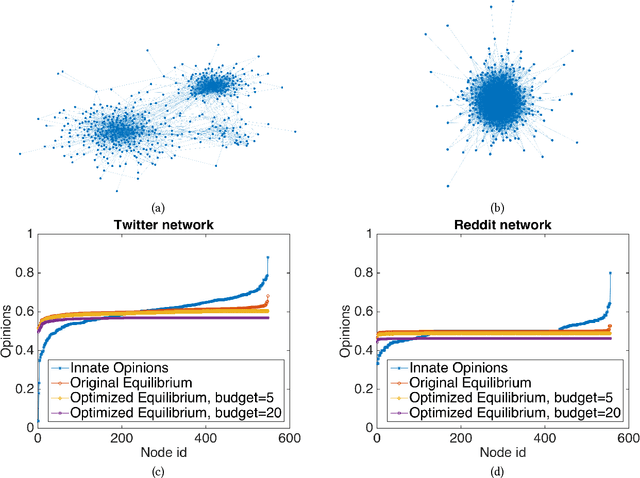
Abstract:The rise of social media and online social networks has been a disruptive force in society. Opinions are increasingly shaped by interactions on online social media, and social phenomena including disagreement and polarization are now tightly woven into everyday life. In this work we initiate the study of the following question: given $n$ agents, each with its own initial opinion that reflects its core value on a topic, and an opinion dynamics model, what is the structure of a social network that minimizes {\em polarization} and {\em disagreement} simultaneously? This question is central to recommender systems: should a recommender system prefer a link suggestion between two online users with similar mindsets in order to keep disagreement low, or between two users with different opinions in order to expose each to the other's viewpoint of the world, and decrease overall levels of polarization? Our contributions include a mathematical formalization of this question as an optimization problem and an exact, time-efficient algorithm. We also prove that there always exists a network with $O(n/\epsilon^2)$ edges that is a $(1+\epsilon)$ approximation to the optimum. For a fixed graph, we additionally show how to optimize our objective function over the agents' innate opinions in polynomial time. We perform an empirical study of our proposed methods on synthetic and real-world data that verify their value as mining tools to better understand the trade-off between of disagreement and polarization. We find that there is a lot of space to reduce both polarization and disagreement in real-world networks; for instance, on a Reddit network where users exchange comments on politics, our methods achieve a $\sim 60\,000$-fold reduction in polarization and disagreement.
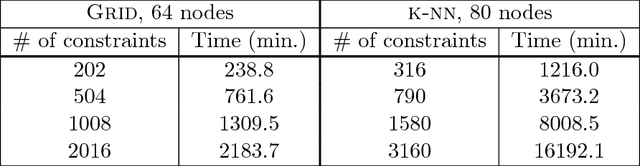
Spectrum Approximation Beyond Fast Matrix Multiplication: Algorithms and Hardness
Nov 20, 2017
Abstract:Understanding the singular value spectrum of a matrix $A \in \mathbb{R}^{n \times n}$ is a fundamental task in countless applications. In matrix multiplication time, it is possible to perform a full SVD and directly compute the singular values $\sigma_1,...,\sigma_n$. However, little is known about algorithms that break this runtime barrier. Using tools from stochastic trace estimation, polynomial approximation, and fast system solvers, we show how to efficiently isolate different ranges of $A$'s spectrum and approximate the number of singular values in these ranges. We thus effectively compute a histogram of the spectrum, which can stand in for the true singular values in many applications. We use this primitive to give the first algorithms for approximating a wide class of symmetric matrix norms in faster than matrix multiplication time. For example, we give a $(1 + \epsilon)$ approximation algorithm for the Schatten-$1$ norm (the nuclear norm) running in just $\tilde O((nnz(A)n^{1/3} + n^2)\epsilon^{-3})$ time for $A$ with uniform row sparsity or $\tilde O(n^{2.18} \epsilon^{-3})$ time for dense matrices. The runtime scales smoothly for general Schatten-$p$ norms, notably becoming $\tilde O (p \cdot nnz(A) \epsilon^{-3})$ for any $p \ge 2$. At the same time, we show that the complexity of spectrum approximation is inherently tied to fast matrix multiplication in the small $\epsilon$ regime. We prove that achieving milder $\epsilon$ dependencies in our algorithms would imply faster than matrix multiplication time triangle detection for general graphs. This further implies that highly accurate algorithms running in subcubic time yield subcubic time matrix multiplication. As an application of our bounds, we show that precisely computing all effective resistances in a graph in less than matrix multiplication time is likely difficult, barring a major algorithmic breakthrough.
Is Input Sparsity Time Possible for Kernel Low-Rank Approximation?
Nov 05, 2017Abstract:Low-rank approximation is a common tool used to accelerate kernel methods: the $n \times n$ kernel matrix $K$ is approximated via a rank-$k$ matrix $\tilde K$ which can be stored in much less space and processed more quickly. In this work we study the limits of computationally efficient low-rank kernel approximation. We show that for a broad class of kernels, including the popular Gaussian and polynomial kernels, computing a relative error $k$-rank approximation to $K$ is at least as difficult as multiplying the input data matrix $A \in \mathbb{R}^{n \times d}$ by an arbitrary matrix $C \in \mathbb{R}^{d \times k}$. Barring a breakthrough in fast matrix multiplication, when $k$ is not too large, this requires $\Omega(nnz(A)k)$ time where $nnz(A)$ is the number of non-zeros in $A$. This lower bound matches, in many parameter regimes, recent work on subquadratic time algorithms for low-rank approximation of general kernels [MM16,MW17], demonstrating that these algorithms are unlikely to be significantly improved, in particular to $O(nnz(A))$ input sparsity runtimes. At the same time there is hope: we show for the first time that $O(nnz(A))$ time approximation is possible for general radial basis function kernels (e.g., the Gaussian kernel) for the closely related problem of low-rank approximation of the kernelized dataset.
Recursive Sampling for the Nyström Method
Nov 03, 2017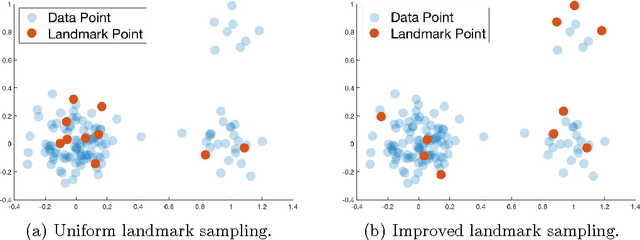
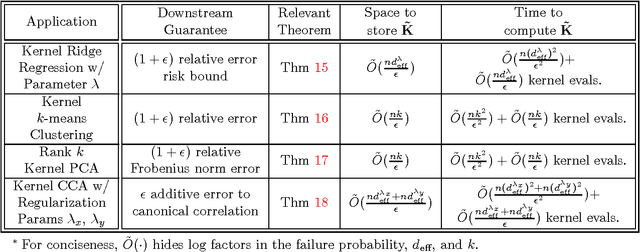
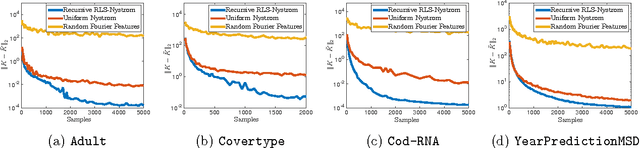
Abstract:We give the first algorithm for kernel Nystr\"om approximation that runs in *linear time in the number of training points* and is provably accurate for all kernel matrices, without dependence on regularity or incoherence conditions. The algorithm projects the kernel onto a set of $s$ landmark points sampled by their *ridge leverage scores*, requiring just $O(ns)$ kernel evaluations and $O(ns^2)$ additional runtime. While leverage score sampling has long been known to give strong theoretical guarantees for Nystr\"om approximation, by employing a fast recursive sampling scheme, our algorithm is the first to make the approach scalable. Empirically we show that it finds more accurate, lower rank kernel approximations in less time than popular techniques such as uniformly sampled Nystr\"om approximation and the random Fourier features method.
Neuro-RAM Unit with Applications to Similarity Testing and Compression in Spiking Neural Networks
Aug 21, 2017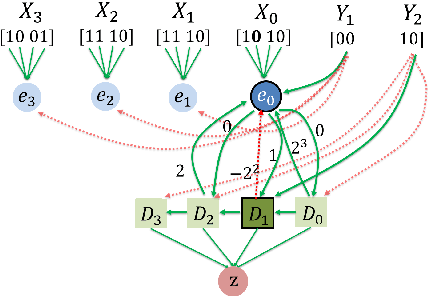
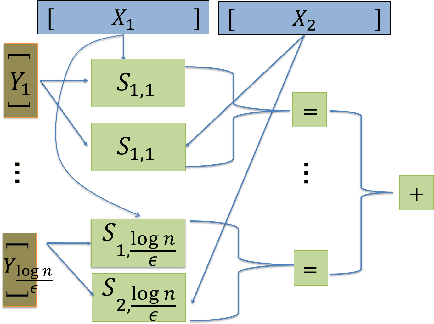
Abstract:We study distributed algorithms implemented in a simplified biologically inspired model for stochastic spiking neural networks. We focus on tradeoffs between computation time and network complexity, along with the role of randomness in efficient neural computation. It is widely accepted that neural computation is inherently stochastic. In recent work, we explored how this stochasticity could be leveraged to solve the `winner-take-all' leader election task. Here, we focus on using randomness in neural algorithms for similarity testing and compression. In the most basic setting, given two $n$-length patterns of firing neurons, we wish to distinguish if the patterns are equal or $\epsilon$-far from equal. Randomization allows us to solve this task with a very compact network, using $O \left (\frac{\sqrt{n}\log n}{\epsilon}\right)$ auxiliary neurons, which is sublinear in the input size. At the heart of our solution is the design of a $t$-round neural random access memory, or indexing network, which we call a neuro-RAM. This module can be implemented with $O(n/t)$ auxiliary neurons and is useful in many applications beyond similarity testing. Using a VC dimension-based argument, we show that the tradeoff between runtime and network size in our neuro-RAM is nearly optimal. Our result has several implications -- since our neuro-RAM can be implemented with deterministic threshold gates, it shows that, in contrast to similarity testing, randomness does not provide significant computational advantages for this problem. It also establishes a separation between feedforward networks whose gates spike with sigmoidal probability functions, and well-studied deterministic sigmoidal networks, whose gates output real number sigmoidal values, and which can implement a neuro-RAM much more efficiently.
Sublinear Time Low-Rank Approximation of Positive Semidefinite Matrices
Aug 16, 2017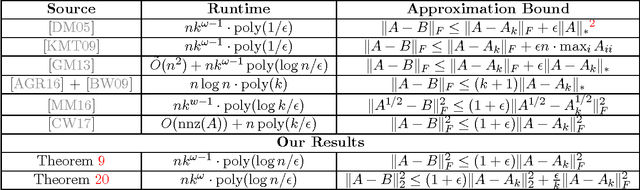
Abstract:We show how to compute a relative-error low-rank approximation to any positive semidefinite (PSD) matrix in sublinear time, i.e., for any $n \times n$ PSD matrix $A$, in $\tilde O(n \cdot poly(k/\epsilon))$ time we output a rank-$k$ matrix $B$, in factored form, for which $\|A-B\|_F^2 \leq (1+\epsilon)\|A-A_k\|_F^2$, where $A_k$ is the best rank-$k$ approximation to $A$. When $k$ and $1/\epsilon$ are not too large compared to the sparsity of $A$, our algorithm does not need to read all entries of the matrix. Hence, we significantly improve upon previous $nnz(A)$ time algorithms based on oblivious subspace embeddings, and bypass an $nnz(A)$ time lower bound for general matrices (where $nnz(A)$ denotes the number of non-zero entries in the matrix). We prove time lower bounds for low-rank approximation of PSD matrices, showing that our algorithm is close to optimal. Finally, we extend our techniques to give sublinear time algorithms for low-rank approximation of $A$ in the (often stronger) spectral norm metric $\|A-B\|_2^2$ and for ridge regression on PSD matrices.
Input Sparsity Time Low-Rank Approximation via Ridge Leverage Score Sampling
Oct 06, 2016Abstract:We present a new algorithm for finding a near optimal low-rank approximation of a matrix $A$ in $O(nnz(A))$ time. Our method is based on a recursive sampling scheme for computing a representative subset of $A$'s columns, which is then used to find a low-rank approximation. This approach differs substantially from prior $O(nnz(A))$ time algorithms, which are all based on fast Johnson-Lindenstrauss random projections. It matches the guarantees of these methods while offering a number of advantages. Not only are sampling algorithms faster for sparse and structured data, but they can also be applied in settings where random projections cannot. For example, we give new single-pass streaming algorithms for the column subset selection and projection-cost preserving sample problems. Our method has also been used to give the fastest algorithms for provably approximating kernel matrices [MM16].
Computational Tradeoffs in Biological Neural Networks: Self-Stabilizing Winner-Take-All Networks
Oct 06, 2016
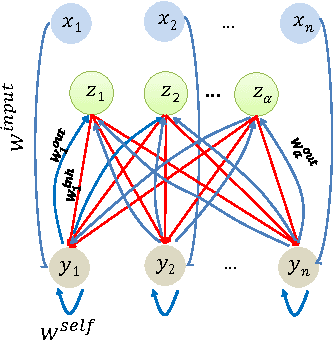
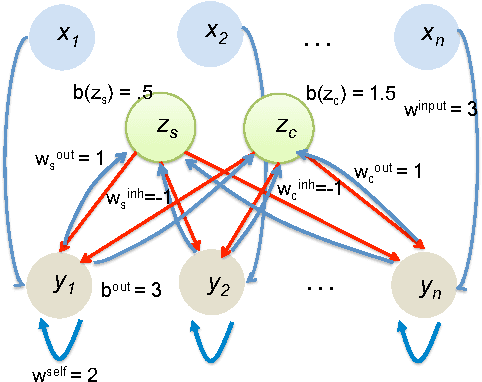
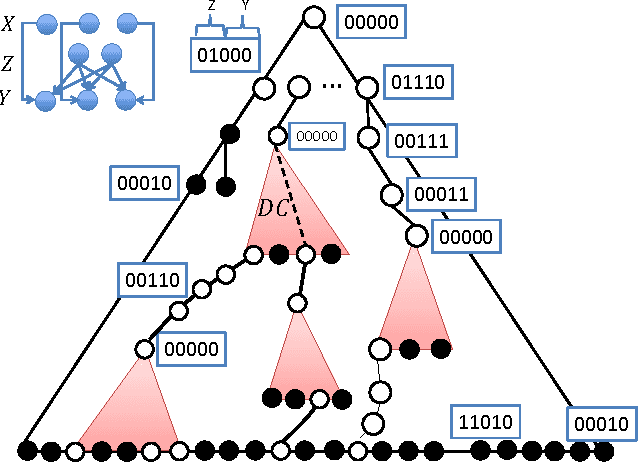
Abstract:We initiate a line of investigation into biological neural networks from an algorithmic perspective. We develop a simplified but biologically plausible model for distributed computation in stochastic spiking neural networks and study tradeoffs between computation time and network complexity in this model. Our aim is to abstract real neural networks in a way that, while not capturing all interesting features, preserves high-level behavior and allows us to make biologically relevant conclusions. In this paper, we focus on the important `winner-take-all' (WTA) problem, which is analogous to a neural leader election unit: a network consisting of $n$ input neurons and $n$ corresponding output neurons must converge to a state in which a single output corresponding to a firing input (the `winner') fires, while all other outputs remain silent. Neural circuits for WTA rely on inhibitory neurons, which suppress the activity of competing outputs and drive the network towards a converged state with a single firing winner. We attempt to understand how the number of inhibitors used affects network convergence time. We show that it is possible to significantly outperform naive WTA constructions through a more refined use of inhibition, solving the problem in $O(\theta)$ rounds in expectation with just $O(\log^{1/\theta} n)$ inhibitors for any $\theta$. An alternative construction gives convergence in $O(\log^{1/\theta} n)$ rounds with $O(\theta)$ inhibitors. We compliment these upper bounds with our main technical contribution, a nearly matching lower bound for networks using $\ge \log\log n$ inhibitors. Our lower bound uses familiar indistinguishability and locality arguments from distributed computing theory. It lets us derive a number of interesting conclusions about the structure of any network solving WTA with good probability, and the use of randomness and inhibition within such a network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge