Nanobot Algorithms for Treatment of Diffuse Cancer

Motile nanosized particles, or "nanobots", promise more effective and less toxic targeted drug delivery because of their unique scale and precision. We consider the case in which the cancer is "diffuse", dispersed such that there are multiple distinct cancer sites. We investigate the problem of a swarm of nanobots locating these sites and treating them by dropping drug payloads at the sites. To improve the success of the treatment, the drug payloads must be allocated between sites according to their "demands"; this requires extra nanobot coordination. We present a mathematical model of the behavior of the nanobot agents and of their colloidal environment. This includes a movement model for agents based upon experimental findings from actual nanoparticles in which bots noisily ascend and descend chemical gradients. We present three algorithms: The first algorithm, called KM, is the most representative of reality, with agents simply following naturally existing chemical signals that surround each cancer site. The second algorithm, KMA, includes an additional chemical payload which amplifies the existing natural signals. The third algorithm, KMAR, includes another additional chemical payload which counteracts the other signals, instead inducing negative chemotaxis in agents such that they are repelled from sites that are already sufficiently treated. We present simulation results for all algorithms across different types of cancer arrangements. For KM, we show that the treatment is generally successful unless the natural chemical signals are weak, in which case the treatment progresses too slowly. For KMA, we demonstrate a significant improvement in treatment speed but a drop in eventual success, except for concentrated cancer patterns. For KMAR, our results show great performance across all types of cancer patterns, demonstrating robustness and adaptability.

Swarm Algorithms for Dynamic Task Allocation in Unknown Environments

Robot swarms, systems of many robots that operate in a distributed fashion, have many applications in areas such as search-and-rescue, natural disaster response, and self-assembly. Several of these applications can be abstracted to the general problem of task allocation in an environment, in which robots must assign themselves to and complete tasks. While several algorithms for task allocation have been proposed, most of them assume either prior knowledge of task locations or a static set of tasks. Operating under a discrete general model where tasks dynamically appear in unknown locations, we present three new swarm algorithms for task allocation. We demonstrate that when tasks appear slowly, our variant of a distributed algorithm based on propagating task information completes tasks more efficiently than a Levy random walk algorithm, which is a strategy used by many organisms in nature to efficiently search an environment. We also propose a division of labor algorithm where some agents are using our algorithm based on propagating task information while the remaining agents are using the Levy random walk algorithm. Finally, we introduce a hybrid algorithm where each agent dynamically switches between using propagated task information and following a Levy random walk. We show that our division of labor and hybrid algorithms can perform better than both our algorithm based on propagated task information and the Levy walk algorithm, especially at low and medium task rates. When tasks appear fast, we observe the Levy random walk strategy performs as well or better when compared to these novel approaches. Our work demonstrates the relative performance of these algorithms on a variety of task rates and also provide insight into optimizing our algorithms based on environment parameters.

Abstraction in Neural Networks

We show how brain networks, modeled as Spiking Neural Networks, can be viewed at different levels of abstraction. Lower levels include complications such as failures of neurons and edges. Higher levels are more abstract, making simplifying assumptions to avoid these complications. We show precise relationships between executions of networks at different levels, which enables us to understand the behavior of lower-level networks in terms of the behavior of higher-level networks. We express our results using two abstract networks, A1 and A2, one to express firing guarantees and the other to express non-firing guarantees, and one detailed network D. The abstract networks contain reliable neurons and edges, whereas the detailed network has neurons and edges that may fail, subject to some constraints. Here we consider just initial stopping failures. To define these networks, we begin with abstract network A1 and modify it systematically to obtain the other two networks. To obtain A2, we simply lower the firing thresholds of the neurons. To obtain D, we introduce failures of neurons and edges, and incorporate redundancy in the neurons and edges in order to compensate for the failures. We also define corresponding inputs for the networks, and corresponding executions of the networks. We prove two main theorems, one relating corresponding executions of A1 and D and the other relating corresponding executions of A2 and D. Together, these give both firing and non-firing guarantees for the detailed network D. We also give a third theorem, relating the effects of D on an external reliable actuator neuron to the effects of the abstract networks on the same actuator neuron.

Learning Hierarchically-Structured Concepts II: Overlapping Concepts, and Networks With Feedback

We continue our study from Lynch and Mallmann-Trenn (Neural Networks, 2021), of how concepts that have hierarchical structure might be represented in brain-like neural networks, how these representations might be used to recognize the concepts, and how these representations might be learned. In Lynch and Mallmann-Trenn (Neural Networks, 2021), we considered simple tree-structured concepts and feed-forward layered networks. Here we extend the model in two ways: we allow limited overlap between children of different concepts, and we allow networks to include feedback edges. For these more general cases, we describe and analyze algorithms for recognition and algorithms for learning.

A Comparison of New Swarm Task Allocation Algorithms in Unknown Environments with Varying Task Density

Task allocation is an important problem for robot swarms to solve, allowing agents to reduce task completion time by performing tasks in a distributed fashion. Existing task allocation algorithms often assume prior knowledge of task location and demand or fail to consider the effects of the geometric distribution of tasks on the completion time and communication cost of the algorithms. In this paper, we examine an environment where agents must explore and discover tasks with positive demand and successfully assign themselves to complete all such tasks. We propose two new task allocation algorithms for initially unknown environments -- one based on N-site selection and the other on virtual pheromones. We analyze each algorithm separately and also evaluate the effectiveness of the two algorithms in dense vs. sparse task distributions. Compared to the Levy walk, which has been theorized to be optimal for foraging, our virtual pheromone inspired algorithm is much faster in sparse to medium task densities but is communication and agent intensive. Our site selection inspired algorithm also outperforms Levy walk in sparse task densities and is a less resource-intensive option than our virtual pheromone algorithm for this case. Because the performance of both algorithms relative to random walk is dependent on task density, our results shed light on how task density is important in choosing a task allocation algorithm in initially unknown environments.

A superconducting nanowire spiking element for neural networks

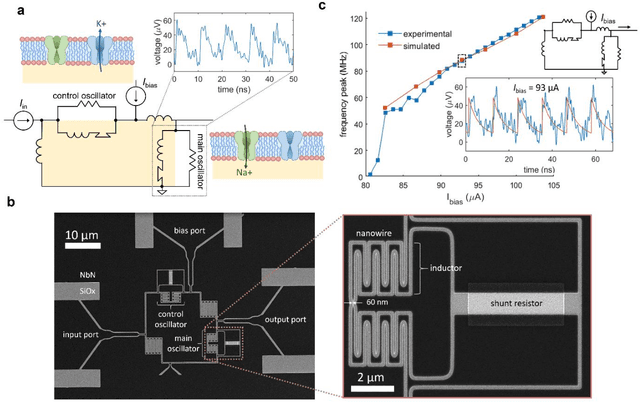
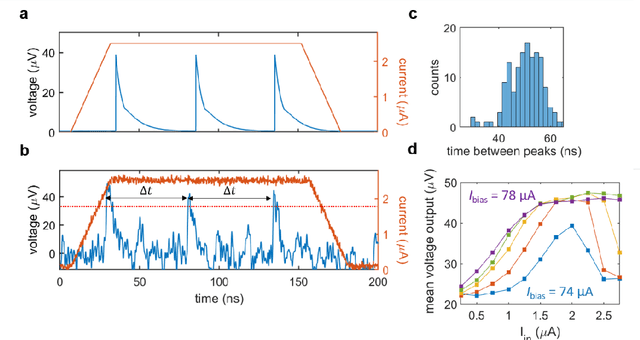
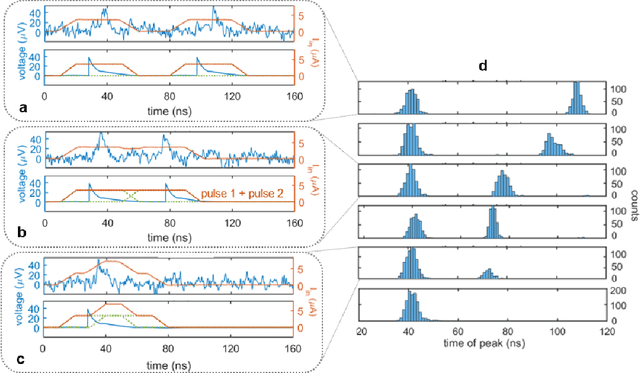
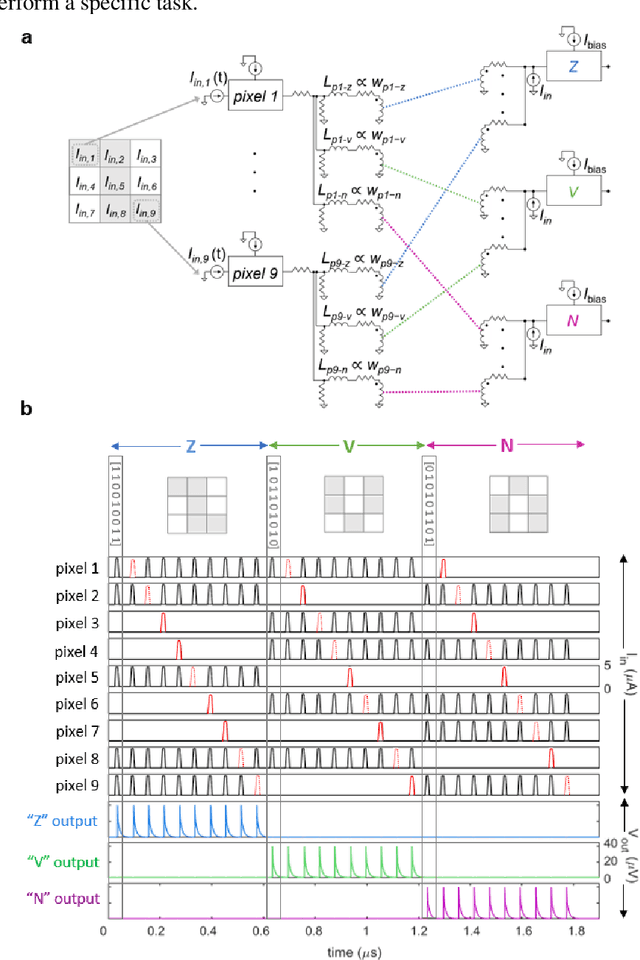
As the limits of traditional von Neumann computing come into view, the brain's ability to communicate vast quantities of information using low-power spikes has become an increasing source of inspiration for alternative architectures. Key to the success of these largescale neural networks is a power-efficient spiking element that is scalable and easily interfaced with traditional control electronics. In this work, we present a spiking element fabricated from superconducting nanowires that has pulse energies on the order of ~10 aJ. We demonstrate that the device reproduces essential characteristics of biological neurons, such as a refractory period and a firing threshold. Through simulations using experimentally measured device parameters, we show how nanowire-based networks may be used for inference in image recognition, and that the probabilistic nature of nanowire switching may be exploited for modeling biological processes and for applications that rely on stochasticity.

Learning Hierarchically Structured Concepts

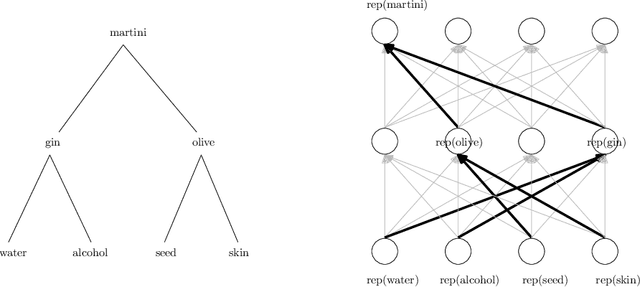
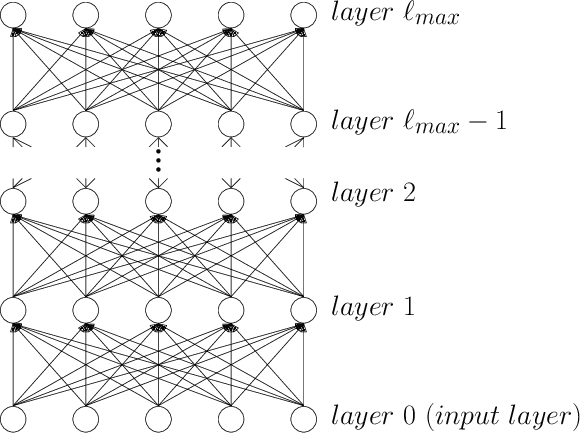
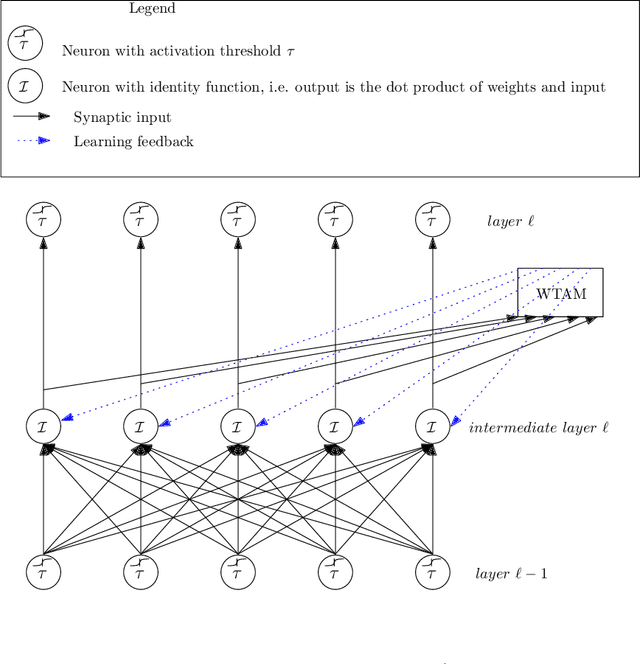
We study the question of how concepts that have structure get represented in the brain. Specifically, we introduce a model for hierarchically structured concepts and we show how a biologically plausible neural network can recognize these concepts, and how it can learn them in the first place. Our main goal is to introduce a general framework for these tasks and prove formally how both (recognition and learning) can be achieved. We show that both tasks can be accomplished even in presence of noise. For learning, we analyze Oja's rule formally, a well-known biologically-plausible rule for adjusting the weights of synapses. We complement the learning results with lower bounds asserting that, in order to recognize concepts of a certain hierarchical depth, neural networks must have a corresponding number of layers.

Winner-Take-All Computation in Spiking Neural Networks

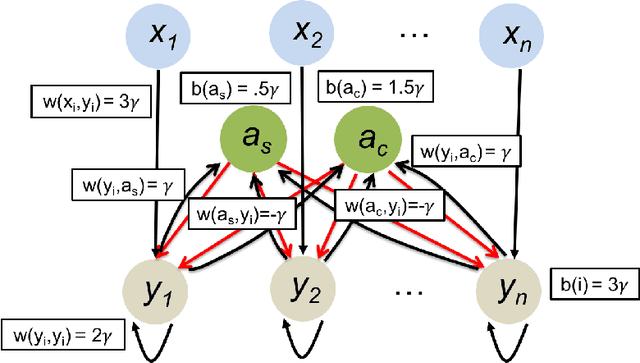
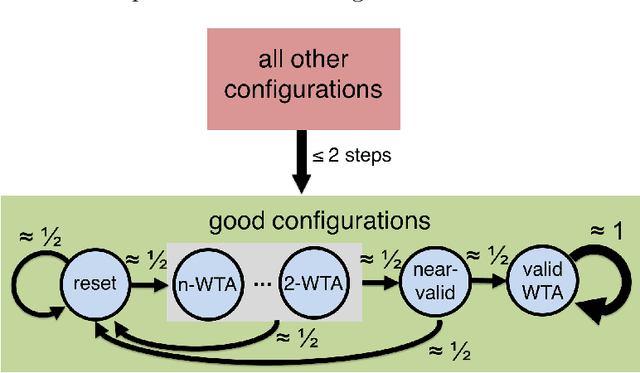
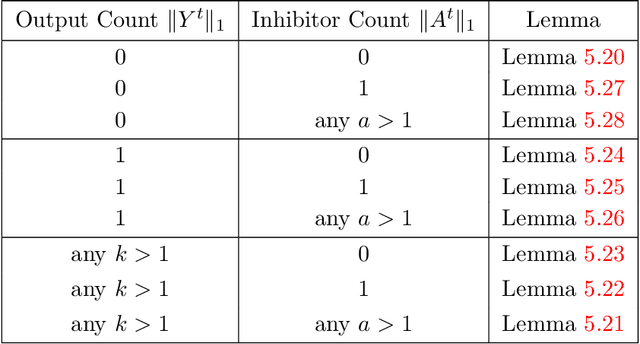
In this work we study biological neural networks from an algorithmic perspective, focusing on understanding tradeoffs between computation time and network complexity. Our goal is to abstract real neural networks in a way that, while not capturing all interesting features, preserves high-level behavior and allows us to make biologically relevant conclusions. Towards this goal, we consider the implementation of algorithmic primitives in a simple yet biologically plausible model of $stochastic\ spiking\ neural\ networks$. In particular, we show how the stochastic behavior of neurons in this model can be leveraged to solve a basic $symmetry-breaking\ task$ in which we are given neurons with identical firing rates and want to select a distinguished one. In computational neuroscience, this is known as the winner-take-all (WTA) problem, and it is believed to serve as a basic building block in many tasks, e.g., learning, pattern recognition, and clustering. We provide efficient constructions of WTA circuits in our stochastic spiking neural network model, as well as lower bounds in terms of the number of auxiliary neurons required to drive convergence to WTA in a given number of steps. These lower bounds demonstrate that our constructions are near-optimal in some cases. This work covers and gives more in-depth proofs of a subset of results originally published in [LMP17a]. It is adapted from the last chapter of C. Musco's Ph.D. thesis [Mus18].

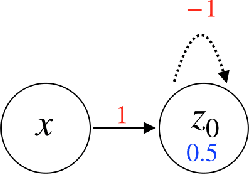
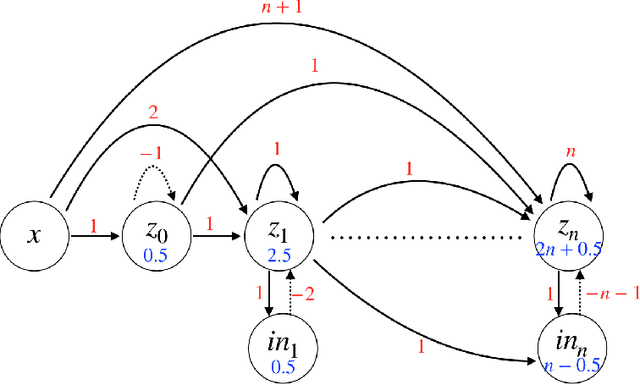
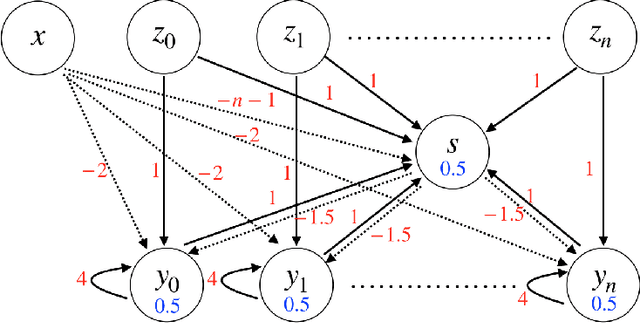
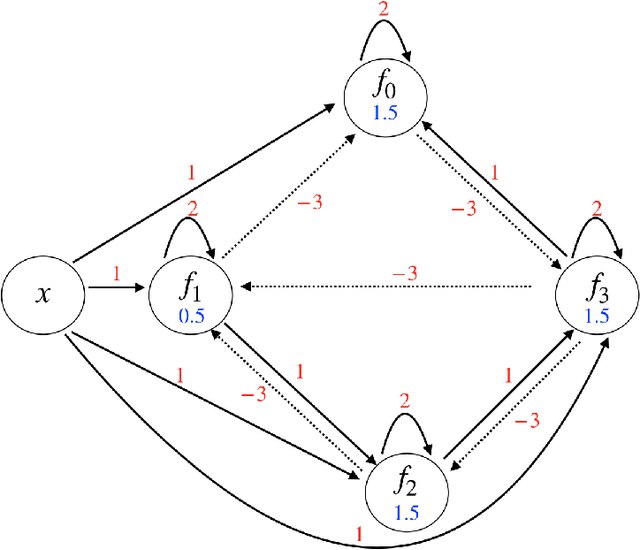
Integrating Temporal Information to Spatial Information in a Neural Circuit

In this paper, we consider a network of spiking neurons with a deterministic synchronous firing rule at discrete time. We propose three problems -- "first consecutive spikes counting", "total spikes counting" and "$k$-spikes temporal to spatial encoding" -- to model how brains extract temporal information into spatial information from different neural codings. For a max input length $T$, we design three networks that solve these three problems with matching lower bounds in both time $O(T)$ and number of neurons $O(\log T)$ in all three questions.

A Basic Compositional Model for Spiking Neural Networks

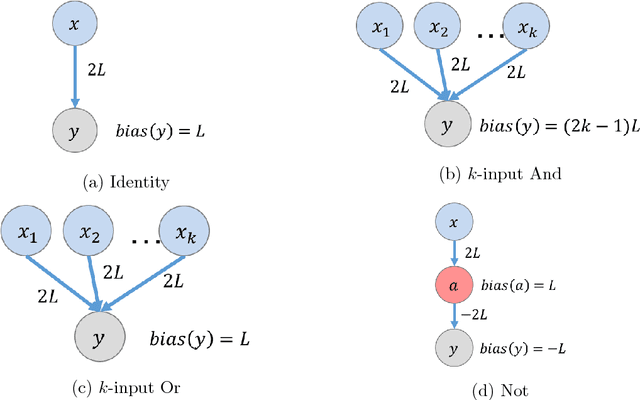
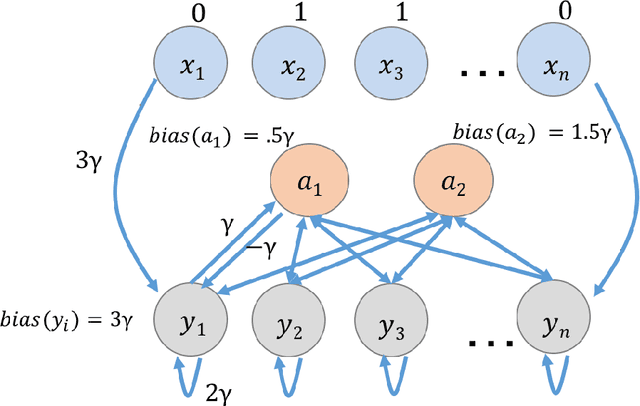
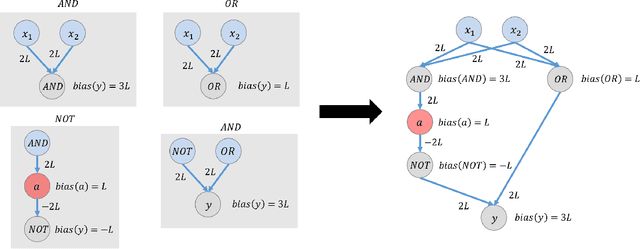
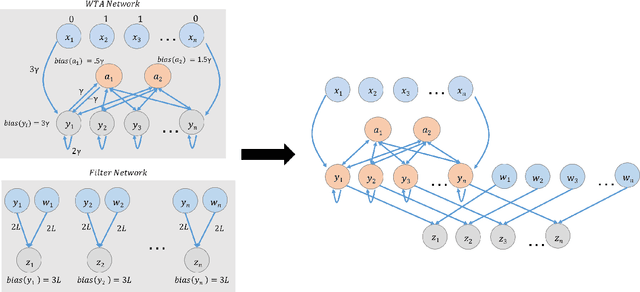
This paper is part of a project on developing an algorithmic theory of brain networks, based on stochastic Spiking Neural Network (SNN) models. Inspired by tasks that seem to be solved in actual brains, we are defining abstract problems to be solved by these networks. In our work so far, we have developed models and algorithms for the Winner-Take-All problem from computational neuroscience [LMP17a,Mus18], and problems of similarity detection and neural coding [LMP17b]. We plan to consider many other problems and networks, including both static networks and networks that learn. This paper is about basic theory for the stochastic SNN model. In particular, we define a simple version of the model. This version assumes that the neurons' only state is a Boolean, indicating whether the neuron is firing or not. In later work, we plan to develop variants of the model with more elaborate state. We also define an external behavior notion for SNNs, which can be used for stating requirements to be satisfied by the networks. We then define a composition operator for SNNs. We prove that our external behavior notion is "compositional", in the sense that the external behavior of a composed network depends only on the external behaviors of the component networks. We also define a hiding operator that reclassifies some output behavior of an SNN as internal. We give basic results for hiding. Finally, we give a formal definition of a problem to be solved by an SNN, and give basic results showing how composition and hiding of networks affect the problems that they solve. We illustrate our definitions with three examples: building a circuit out of gates, building an "Attention" network out of a "Winner-Take-All" network and a "Filter" network, and a toy example involving combining two networks in a cyclic fashion.