ULTRA-MC: A Unified Approach to Learning Mixtures of Markov Chains via Hitting Times

This study introduces a novel approach for learning mixtures of Markov chains, a critical process applicable to various fields, including healthcare and the analysis of web users. Existing research has identified a clear divide in methodologies for learning mixtures of discrete and continuous-time Markov chains, while the latter presents additional complexities for recovery accuracy and efficiency. We introduce a unifying strategy for learning mixtures of discrete and continuous-time Markov chains, focusing on hitting times, which are well defined for both types. Specifically, we design a reconstruction algorithm that outputs a mixture which accurately reflects the estimated hitting times and demonstrates resilience to noise. We introduce an efficient gradient-descent approach, specifically tailored to manage the computational complexity and non-symmetric characteristics inherent in the calculation of hitting time derivatives. Our approach is also of significant interest when applied to a single Markov chain, thus extending the methodologies previously established by Hoskins et al. and Wittmann et al. We complement our theoretical work with experiments conducted on synthetic and real-world datasets, providing a comprehensive evaluation of our methodology.

Markovletics: Methods and A Novel Application for Learning Continuous-Time Markov Chain Mixtures

Sequential data naturally arises from user engagement on digital platforms like social media, music streaming services, and web navigation, encapsulating evolving user preferences and behaviors through continuous information streams. A notable unresolved query in stochastic processes is learning mixtures of continuous-time Markov chains (CTMCs). While there is progress in learning mixtures of discrete-time Markov chains with recovery guarantees [GKV16,ST23,KTT2023], the continuous scenario uncovers unique unexplored challenges. The intrigue in CTMC mixtures stems from their potential to model intricate continuous-time stochastic processes prevalent in various fields including social media, finance, and biology. In this study, we introduce a novel framework for exploring CTMCs, emphasizing the influence of observed trails' length and mixture parameters on problem regimes, which demands specific algorithms. Through thorough experimentation, we examine the impact of discretizing continuous-time trails on the learnability of the continuous-time mixture, given that these processes are often observed via discrete, resource-demanding observations. Our comparative analysis with leading methods explores sample complexity and the trade-off between the number of trails and their lengths, offering crucial insights for method selection in different problem instances. We apply our algorithms on an extensive collection of Lastfm's user-generated trails spanning three years, demonstrating the capability of our algorithms to differentiate diverse user preferences. We pioneer the use of CTMC mixtures on a basketball passing dataset to unveil intricate offensive tactics of NBA teams. This underscores the pragmatic utility and versatility of our proposed framework. All results presented in this study are replicable, and we provide the implementations to facilitate reproducibility.

Learning Mixtures of Markov Chains with Quality Guarantees

A large number of modern applications ranging from listening songs online and browsing the Web to using a navigation app on a smartphone generate a plethora of user trails. Clustering such trails into groups with a common sequence pattern can reveal significant structure in human behavior that can lead to improving user experience through better recommendations, and even prevent suicides [LMCR14]. One approach to modeling this problem mathematically is as a mixture of Markov chains. Recently, Gupta, Kumar and Vassilvitski [GKV16] introduced an algorithm (GKV-SVD) based on the singular value decomposition (SVD) that under certain conditions can perfectly recover a mixture of L chains on n states, given only the distribution of trails of length 3 (3-trail). In this work we contribute to the problem of unmixing Markov chains by highlighting and addressing two important constraints of the GKV-SVD algorithm [GKV16]: some chains in the mixture may not even be weakly connected, and secondly in practice one does not know beforehand the true number of chains. We resolve these issues in the Gupta et al. paper [GKV16]. Specifically, we propose an algebraic criterion that enables us to choose a value of L efficiently that avoids overfitting. Furthermore, we design a reconstruction algorithm that outputs the true mixture in the presence of disconnected chains and is robust to noise. We complement our theoretical results with experiments on both synthetic and real data, where we observe that our method outperforms the GKV-SVD algorithm. Finally, we empirically observe that combining an EM-algorithm with our method performs best in practice, both in terms of reconstruction error with respect to the distribution of 3-trails and the mixture of Markov Chains.

On the Power of Edge Independent Graph Models

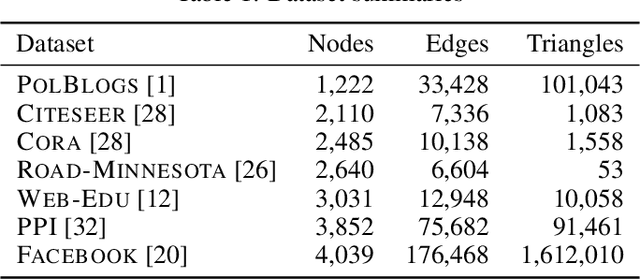
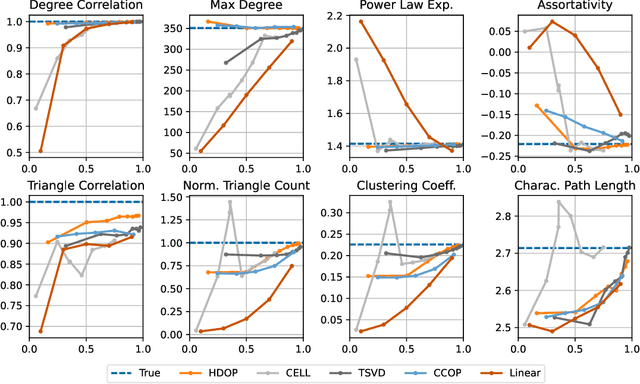
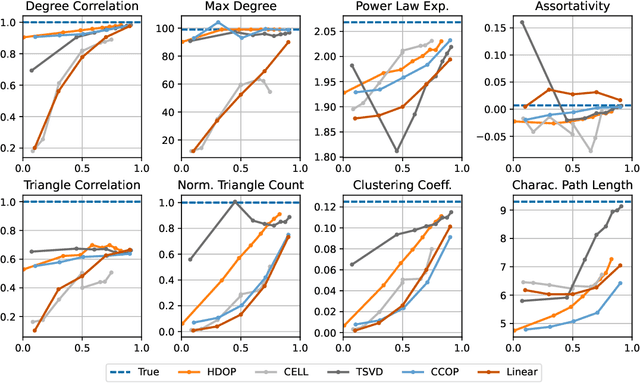
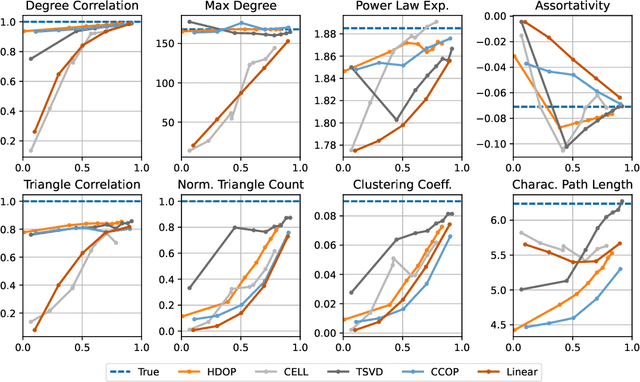
Why do many modern neural-network-based graph generative models fail to reproduce typical real-world network characteristics, such as high triangle density? In this work we study the limitations of edge independent random graph models, in which each edge is added to the graph independently with some probability. Such models include both the classic Erd\"{o}s-R\'{e}nyi and stochastic block models, as well as modern generative models such as NetGAN, variational graph autoencoders, and CELL. We prove that subject to a bounded overlap condition, which ensures that the model does not simply memorize a single graph, edge independent models are inherently limited in their ability to generate graphs with high triangle and other subgraph densities. Notably, such high densities are known to appear in real-world social networks and other graphs. We complement our negative results with a simple generative model that balances overlap and accuracy, performing comparably to more complex models in reconstructing many graph statistics.

DeepWalking Backwards: From Embeddings Back to Graphs

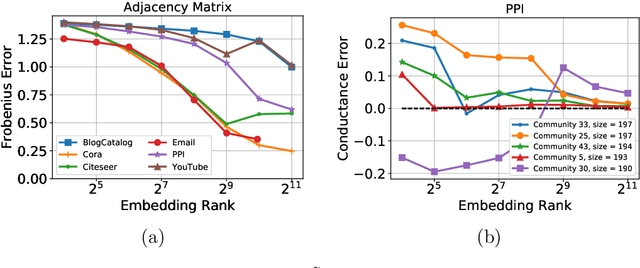
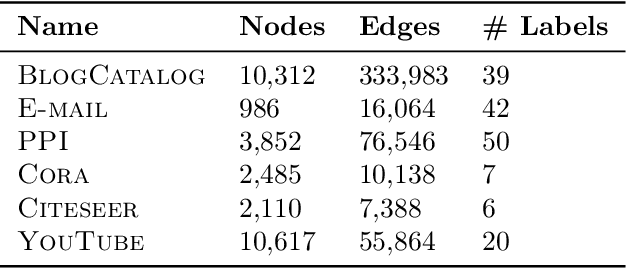
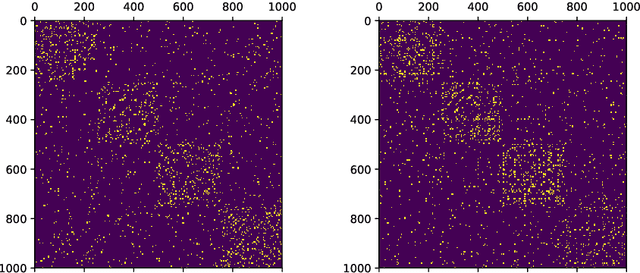
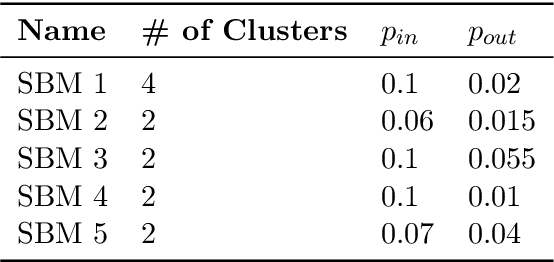
Low-dimensional node embeddings play a key role in analyzing graph datasets. However, little work studies exactly what information is encoded by popular embedding methods, and how this information correlates with performance in downstream machine learning tasks. We tackle this question by studying whether embeddings can be inverted to (approximately) recover the graph used to generate them. Focusing on a variant of the popular DeepWalk method (Perozzi et al., 2014; Qiu et al., 2018), we present algorithms for accurate embedding inversion - i.e., from the low-dimensional embedding of a graph G, we can find a graph H with a very similar embedding. We perform numerous experiments on real-world networks, observing that significant information about G, such as specific edges and bulk properties like triangle density, is often lost in H. However, community structure is often preserved or even enhanced. Our findings are a step towards a more rigorous understanding of exactly what information embeddings encode about the input graph, and why this information is useful for learning tasks.

Node Embeddings and Exact Low-Rank Representations of Complex Networks

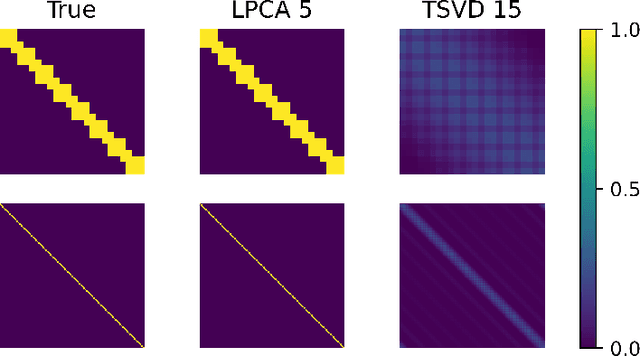
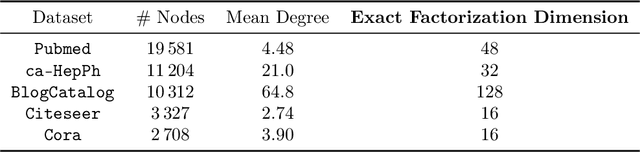
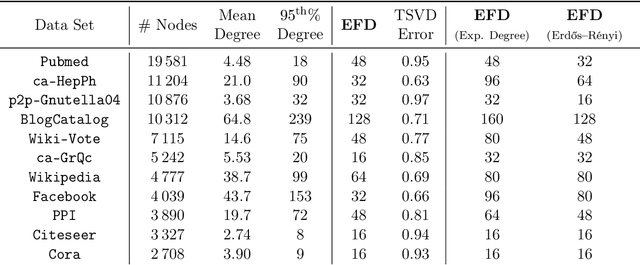
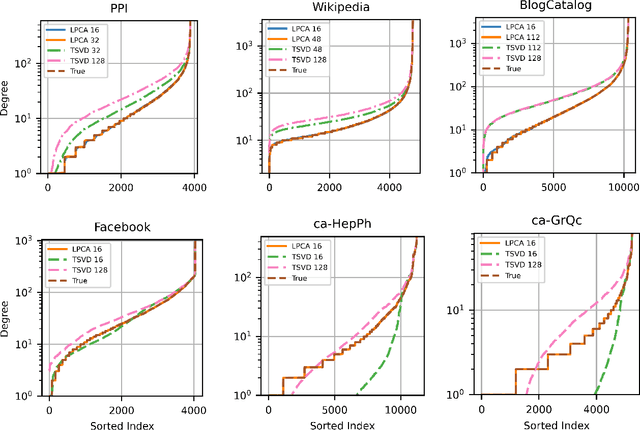
Low-dimensional embeddings, from classical spectral embeddings to modern neural-net-inspired methods, are a cornerstone in the modeling and analysis of complex networks. Recent work by Seshadhri et al. (PNAS 2020) suggests that such embeddings cannot capture local structure arising in complex networks. In particular, they show that any network generated from a natural low-dimensional model cannot be both sparse and have high triangle density (high clustering coefficient), two hallmark properties of many real-world networks. In this work we show that the results of Seshadhri et al. are intimately connected to the model they use rather than the low-dimensional structure of complex networks. Specifically, we prove that a minor relaxation of their model can generate sparse graphs with high triangle density. Surprisingly, we show that this same model leads to exact low-dimensional factorizations of many real-world networks. We give a simple algorithm based on logistic principal component analysis (LPCA) that succeeds in finding such exact embeddings. Finally, we perform a large number of experiments that verify the ability of very low-dimensional embeddings to capture local structure in real-world networks.

Optimal Learning of Joint Alignments with a Faulty Oracle

We consider the following problem, which is useful in applications such as joint image and shape alignment. The goal is to recover $n$ discrete variables $g_i \in \{0, \ldots, k-1\}$ (up to some global offset) given noisy observations of a set of their pairwise differences $\{(g_i - g_j) \bmod k\}$; specifically, with probability $\frac{1}{k}+\delta$ for some $\delta > 0$ one obtains the correct answer, and with the remaining probability one obtains a uniformly random incorrect answer. We consider a learning-based formulation where one can perform a query to observe a pairwise difference, and the goal is to perform as few queries as possible while obtaining the exact joint alignment. We provide an easy-to-implement, time efficient algorithm that performs $O\big(\frac{n \lg n}{k \delta^2}\big)$ queries, and recovers the joint alignment with high probability. We also show that our algorithm is optimal by proving a general lower bound that holds for all non-adaptive algorithms. Our work improves significantly recent work by Chen and Cand\'{e}s \cite{chen2016projected}, who view the problem as a constrained principal components analysis problem that can be solved using the power method. Specifically, our approach is simpler both in the algorithm and the analysis, and provides additional insights into the problem structure.

TwitterMancer: Predicting Interactions on Twitter Accurately

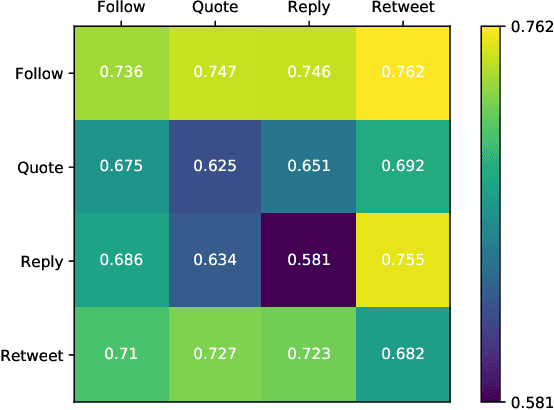
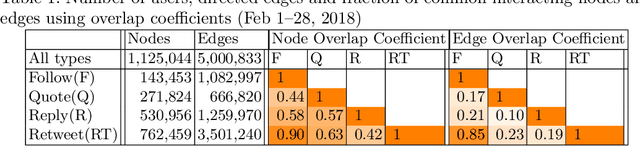
This paper investigates the interplay between different types of user interactions on Twitter, with respect to predicting missing or unseen interactions. For example, given a set of retweet interactions between Twitter users, how accurately can we predict reply interactions? Is it more difficult to predict retweet or quote interactions between a pair of accounts? Also, how important is time locality, and which features of interaction patterns are most important to enable accurate prediction of specific Twitter interactions? Our empirical study of Twitter interactions contributes initial answers to these questions. We have crawled an extensive dataset of Greek-speaking Twitter accounts and their follow, quote, retweet, reply interactions over a period of a month. We find we can accurately predict many interactions of Twitter users. Interestingly, the most predictive features vary with the user profiles, and are not the same across all users. For example, for a pair of users that interact with a large number of other Twitter users, we find that certain "higher-dimensional" triads, i.e., triads that involve multiple types of interactions, are very informative, whereas for less active Twitter users, certain in-degrees and out-degrees play a major role. Finally, we provide various other insights on Twitter user behavior. Our code and data are available at https://github.com/twittermancer/. Keywords: Graph mining, machine learning, social media, social networks

Predicting Positive and Negative Links with Noisy Queries: Theory & Practice

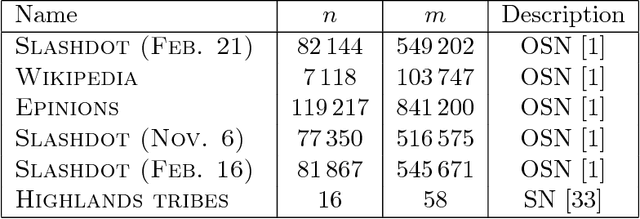
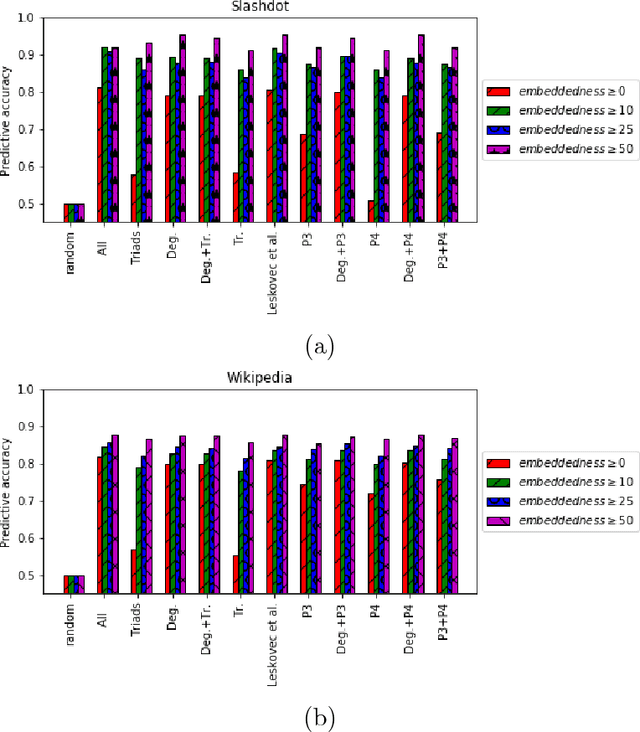
Social networks involve both positive and negative relationships, which can be captured in signed graphs. The {\em edge sign prediction problem} aims to predict whether an interaction between a pair of nodes will be positive or negative. We provide theoretical results for this problem that motivate natural improvements to recent heuristics. The edge sign prediction problem is related to correlation clustering; a positive relationship means being in the same cluster. We consider the following model for two clusters: we are allowed to query any pair of nodes whether they belong to the same cluster or not, but the answer to the query is corrupted with some probability $0<q<\frac{1}{2}$. Let $\delta=1-2q$ be the bias. We provide an algorithm that recovers all signs correctly with high probability in the presence of noise with $O(\frac{n\log n}{\delta^2}+\frac{\log^2 n}{\delta^6})$ queries. This is the best known result for this problem for all but tiny $\delta$, improving on the recent work of Mazumdar and Saha \cite{mazumdar2017clustering}. We also provide an algorithm that performs $O(\frac{n\log n}{\delta^4})$ queries, and uses breadth first search as its main algorithmic primitive. While both the running time and the number of queries for this algorithm are sub-optimal, our result relies on novel theoretical techniques, and naturally suggests the use of edge-disjoint paths as a feature for predicting signs in online social networks. Correspondingly, we experiment with using edge disjoint $s-t$ paths of short length as a feature for predicting the sign of edge $(s,t)$ in real-world signed networks. Empirical findings suggest that the use of such paths improves the classification accuracy, especially for pairs of nodes with no common neighbors.

Opinion Dynamics with Varying Susceptibility to Persuasion

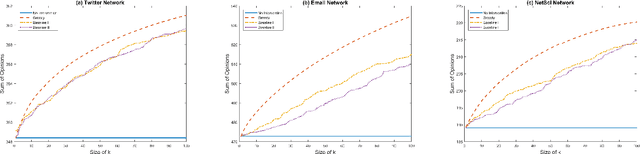
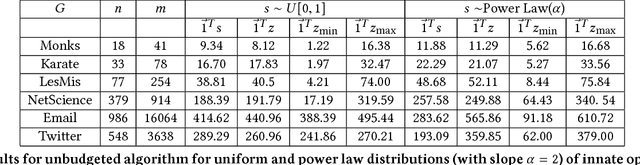
A long line of work in social psychology has studied variations in people's susceptibility to persuasion -- the extent to which they are willing to modify their opinions on a topic. This body of literature suggests an interesting perspective on theoretical models of opinion formation by interacting parties in a network: in addition to considering interventions that directly modify people's intrinsic opinions, it is also natural to consider interventions that modify people's susceptibility to persuasion. In this work, we adopt a popular model for social opinion dynamics, and we formalize the opinion maximization and minimization problems where interventions happen at the level of susceptibility. We show that modeling interventions at the level of susceptibility lead to an interesting family of new questions in network opinion dynamics. We find that the questions are quite different depending on whether there is an overall budget constraining the number of agents we can target or not. We give a polynomial-time algorithm for finding the optimal target-set to optimize the sum of opinions when there are no budget constraints on the size of the target-set. We show that this problem is NP-hard when there is a budget, and that the objective function is neither submodular nor supermodular. Finally, we propose a heuristic for the budgeted opinion optimization and show its efficacy at finding target-sets that optimize the sum of opinions compared on real world networks, including a Twitter network with real opinion estimates.