Learning Networks from Random Walk-Based Node Similarities

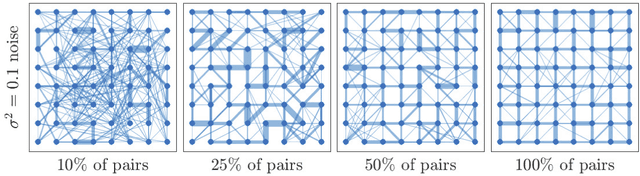
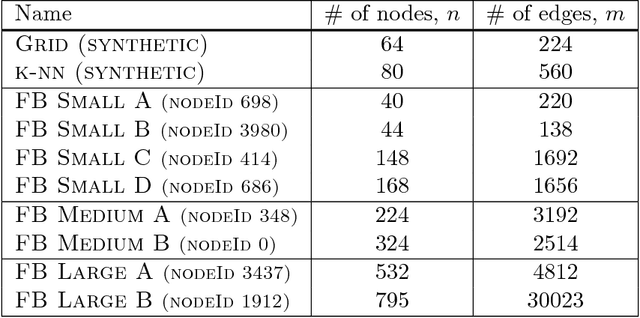
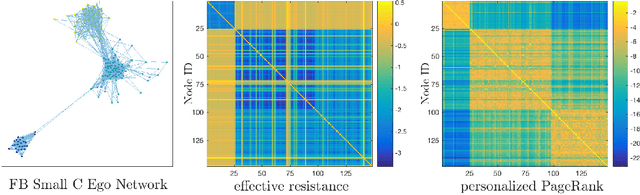
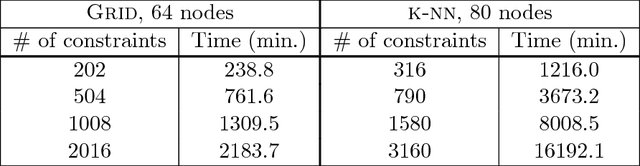
Digital presence in the world of online social media entails significant privacy risks. In this work we consider a privacy threat to a social network in which an attacker has access to a subset of random walk-based node similarities, such as effective resistances (i.e., commute times) or personalized PageRank scores. Using these similarities, the attacker's goal is to infer as much information as possible about the underlying network, including any remaining unknown pairwise node similarities and edges. For the effective resistance metric, we show that with just a small subset of measurements, the attacker can learn a large fraction of edges in a social network, even when the measurements are noisy. We also show that it is possible to learn a graph which accurately matches the underlying network on all other effective resistances. This second observation is interesting from a data mining perspective, since it can be expensive to accurately compute all effective resistances. As an alternative, our graphs learned from just a subset of approximate effective resistances can be used as surrogates in a wide range of applications that use effective resistances to probe graph structure, including for graph clustering, node centrality evaluation, and anomaly detection. We obtain our results by formalizing the graph learning objective mathematically, using two optimization problems. One formulation is convex and can be solved provably in polynomial time. The other is not, but we solve it efficiently with projected gradient and coordinate descent. We demonstrate the effectiveness of these methods on a number of social networks obtained from Facebook. We also discuss how our methods can be generalized to other random walk-based similarities, such as personalized PageRank. Our code is available at https://github.com/cnmusco/graph-similarity-learning.

Efficient Algorithms for t-distributed Stochastic Neighborhood Embedding

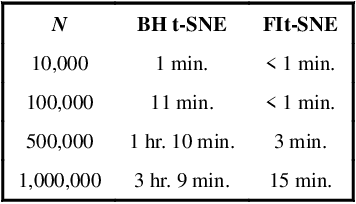
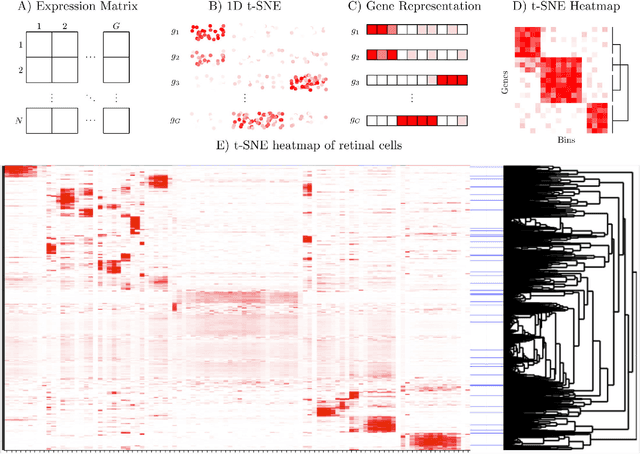
t-distributed Stochastic Neighborhood Embedding (t-SNE) is a method for dimensionality reduction and visualization that has become widely popular in recent years. Efficient implementations of t-SNE are available, but they scale poorly to datasets with hundreds of thousands to millions of high dimensional data-points. We present Fast Fourier Transform-accelerated Interpolation-based t-SNE (FIt-SNE), which dramatically accelerates the computation of t-SNE. The most time-consuming step of t-SNE is a convolution that we accelerate by interpolating onto an equispaced grid and subsequently using the fast Fourier transform to perform the convolution. We also optimize the computation of input similarities in high dimensions using multi-threaded approximate nearest neighbors. We further present a modification to t-SNE called "late exaggeration," which allows for easier identification of clusters in t-SNE embeddings. Finally, for datasets that cannot be loaded into the memory, we present out-of-core randomized principal component analysis (oocPCA), so that the top principal components of a dataset can be computed without ever fully loading the matrix, hence allowing for t-SNE of large datasets to be computed on resource-limited machines.