FLamby: Datasets and Benchmarks for Cross-Silo Federated Learning in Realistic Healthcare Settings

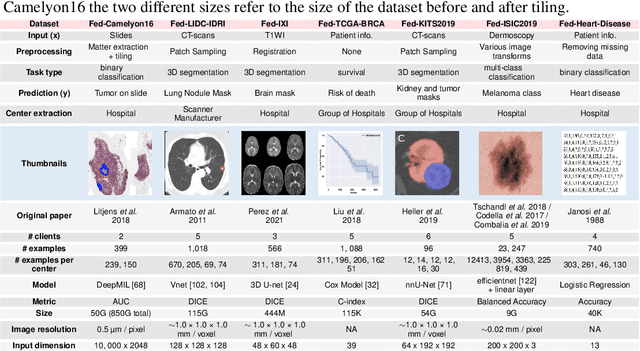
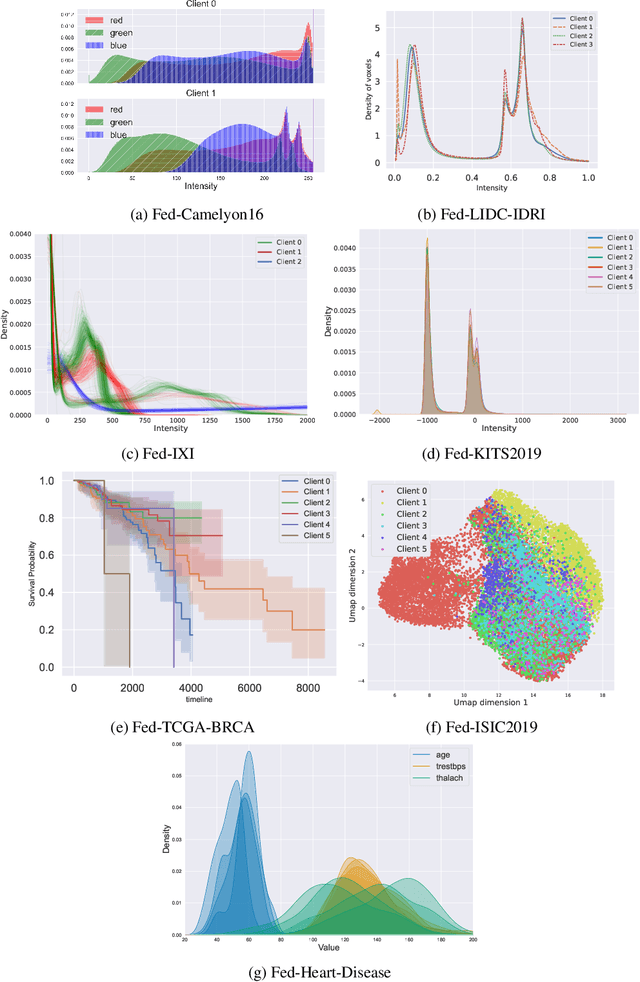
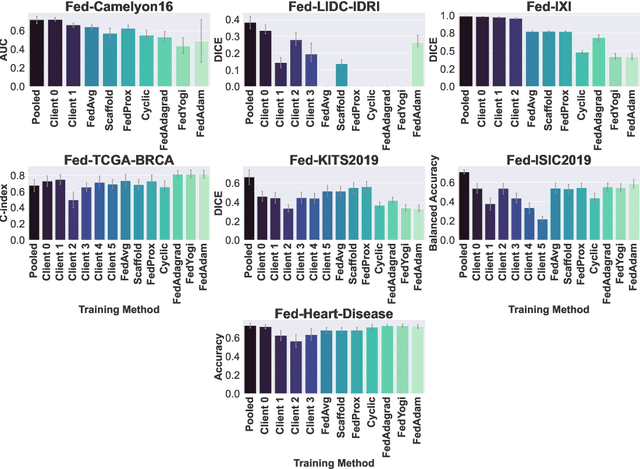
Federated Learning (FL) is a novel approach enabling several clients holding sensitive data to collaboratively train machine learning models, without centralizing data. The cross-silo FL setting corresponds to the case of few ($2$--$50$) reliable clients, each holding medium to large datasets, and is typically found in applications such as healthcare, finance, or industry. While previous works have proposed representative datasets for cross-device FL, few realistic healthcare cross-silo FL datasets exist, thereby slowing algorithmic research in this critical application. In this work, we propose a novel cross-silo dataset suite focused on healthcare, FLamby (Federated Learning AMple Benchmark of Your cross-silo strategies), to bridge the gap between theory and practice of cross-silo FL. FLamby encompasses 7 healthcare datasets with natural splits, covering multiple tasks, modalities, and data volumes, each accompanied with baseline training code. As an illustration, we additionally benchmark standard FL algorithms on all datasets. Our flexible and modular suite allows researchers to easily download datasets, reproduce results and re-use the different components for their research. FLamby is available at~\url{www.github.com/owkin/flamby}.

SecureFedYJ: a safe feature Gaussianization protocol for Federated Learning

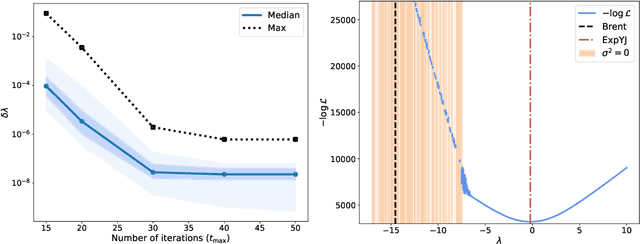
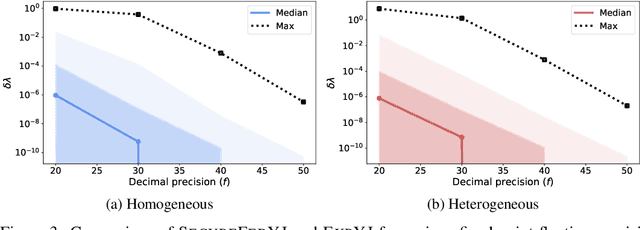
The Yeo-Johnson (YJ) transformation is a standard parametrized per-feature unidimensional transformation often used to Gaussianize features in machine learning. In this paper, we investigate the problem of applying the YJ transformation in a cross-silo Federated Learning setting under privacy constraints. For the first time, we prove that the YJ negative log-likelihood is in fact convex, which allows us to optimize it with exponential search. We numerically show that the resulting algorithm is more stable than the state-of-the-art approach based on the Brent minimization method. Building on this simple algorithm and Secure Multiparty Computation routines, we propose SecureFedYJ, a federated algorithm that performs a pooled-equivalent YJ transformation without leaking more information than the final fitted parameters do. Quantitative experiments on real data demonstrate that, in addition to being secure, our approach reliably normalizes features across silos as well as if data were pooled, making it a viable approach for safe federated feature Gaussianization.

Near-optimal estimation of smooth transport maps with kernel sums-of-squares

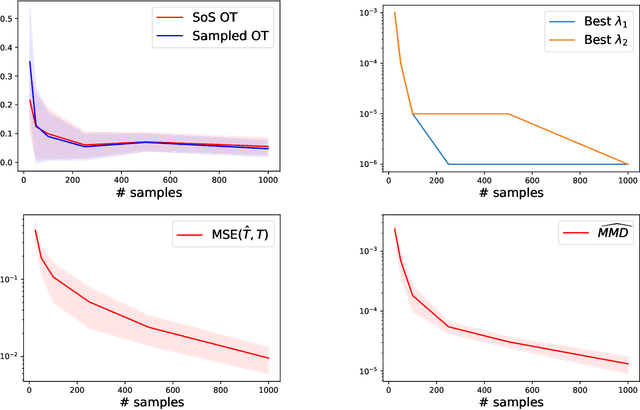
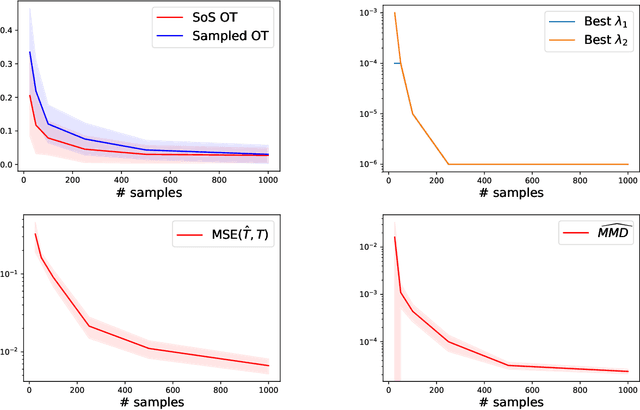
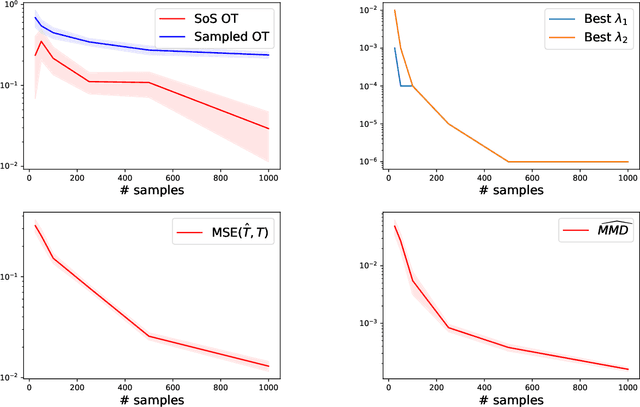
It was recently shown that under smoothness conditions, the squared Wasserstein distance between two distributions could be efficiently computed with appealing statistical error upper bounds. However, rather than the distance itself, the object of interest for applications such as generative modeling is the underlying optimal transport map. Hence, computational and statistical guarantees need to be obtained for the estimated maps themselves. In this paper, we propose the first tractable algorithm for which the statistical $L^2$ error on the maps nearly matches the existing minimax lower-bounds for smooth map estimation. Our method is based on solving the semi-dual formulation of optimal transport with an infinite-dimensional sum-of-squares reformulation, and leads to an algorithm which has dimension-free polynomial rates in the number of samples, with potentially exponentially dimension-dependent constants.

Learning PSD-valued functions using kernel sums-of-squares

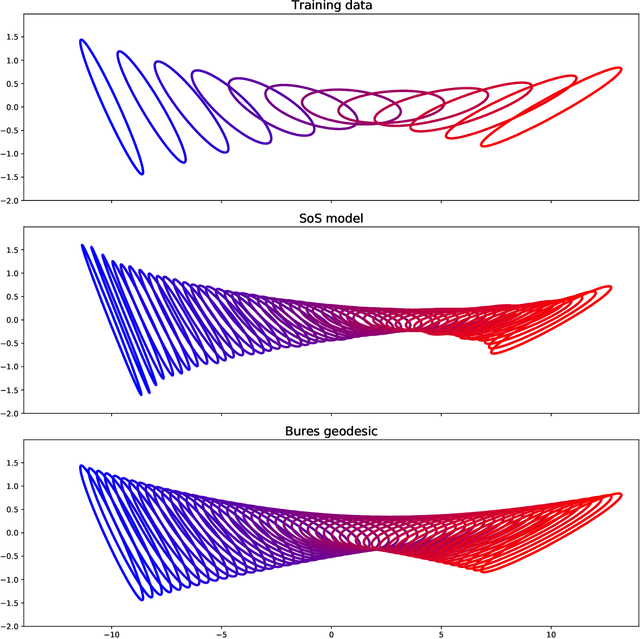
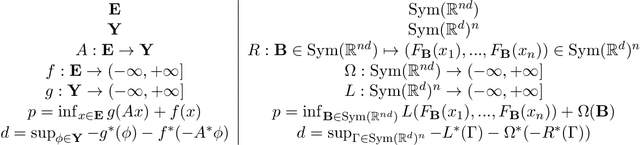
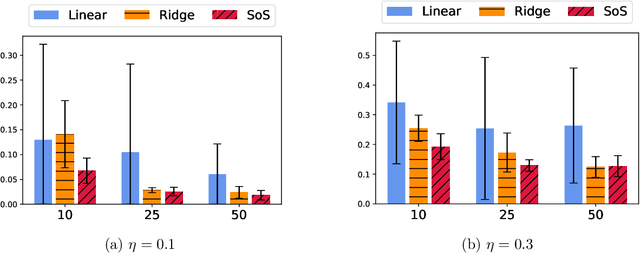
Shape constraints such as positive semi-definiteness (PSD) for matrices or convexity for functions play a central role in many applications in machine learning and sciences, including metric learning, optimal transport, and economics. Yet, very few function models exist that enforce PSD-ness or convexity with good empirical performance and theoretical guarantees. In this paper, we introduce a kernel sum-of-squares model for functions that take values in the PSD cone, which extends kernel sums-of-squares models that were recently proposed to encode non-negative scalar functions. We provide a representer theorem for this class of PSD functions, show that it constitutes a universal approximator of PSD functions, and derive eigenvalue bounds in the case of subsampled equality constraints. We then apply our results to modeling convex functions, by enforcing a kernel sum-of-squares representation of their Hessian, and show that any smooth and strongly convex function may be thus represented. Finally, we illustrate our methods on a PSD matrix-valued regression task, and on scalar-valued convex regression.

A Note on Optimizing Distributions using Kernel Mean Embeddings

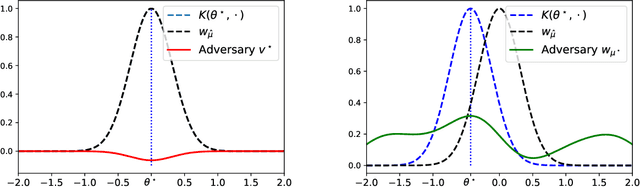
Kernel mean embeddings are a popular tool that consists in representing probability measures by their infinite-dimensional mean embeddings in a reproducing kernel Hilbert space. When the kernel is characteristic, mean embeddings can be used to define a distance between probability measures, known as the maximum mean discrepancy (MMD). A well-known advantage of mean embeddings and MMD is their low computational cost and low sample complexity. However, kernel mean embeddings have had limited applications to problems that consist in optimizing distributions, due to the difficulty of characterizing which Hilbert space vectors correspond to a probability distribution. In this note, we propose to leverage the kernel sums-of-squares parameterization of positive functions of Marteau-Ferey et al. [2020] to fit distributions in the MMD geometry. First, we show that when the kernel is characteristic, distributions with a kernel sum-of-squares density are dense. Then, we provide algorithms to optimize such distributions in the finite-sample setting, which we illustrate in a density fitting numerical experiment.

Dimension-free convergence rates for gradient Langevin dynamics in RKHS

Gradient Langevin dynamics (GLD) and stochastic GLD (SGLD) have attracted considerable attention lately, as a way to provide convergence guarantees in a non-convex setting. However, the known rates grow exponentially with the dimension of the space. In this work, we provide a convergence analysis of GLD and SGLD when the optimization space is an infinite dimensional Hilbert space. More precisely, we derive non-asymptotic, dimension-free convergence rates for GLD/SGLD when performing regularized non-convex optimization in a reproducing kernel Hilbert space. Amongst others, the convergence analysis relies on the properties of a stochastic differential equation, its discrete time Galerkin approximation and the geometric ergodicity of the associated Markov chains.

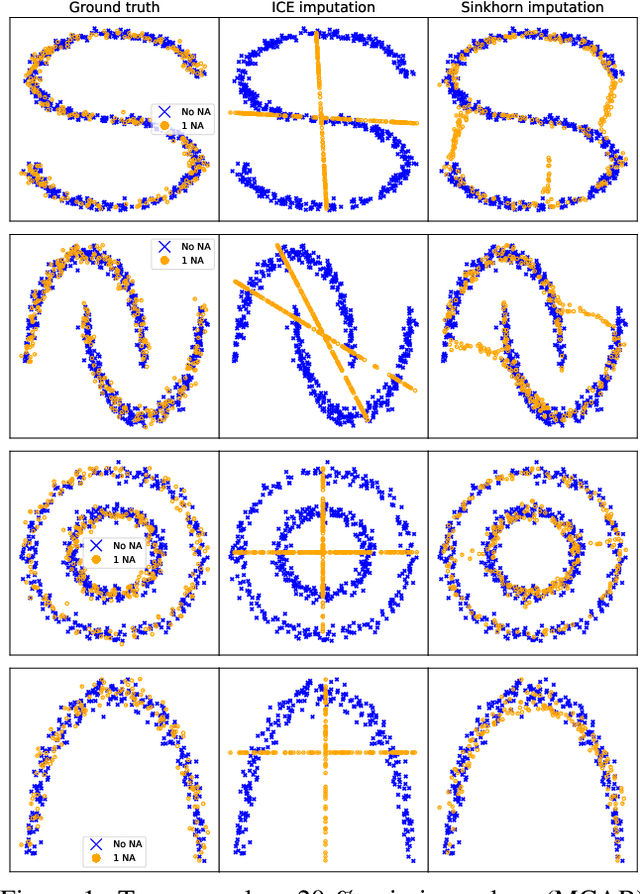
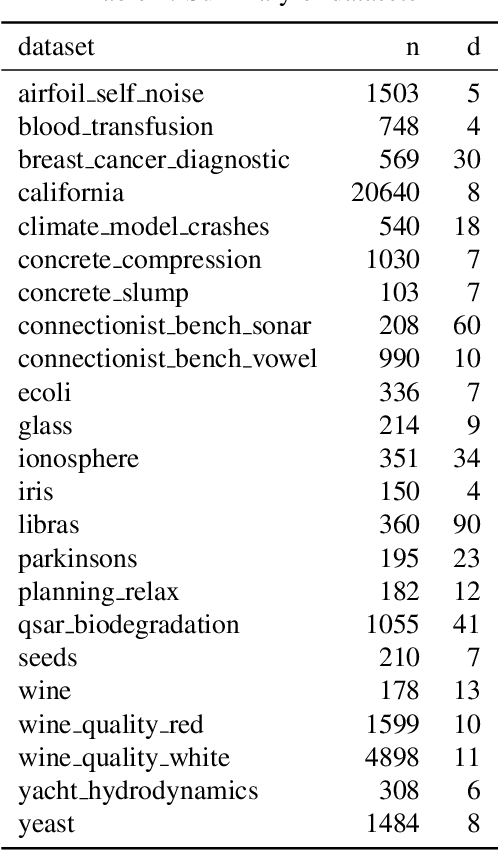
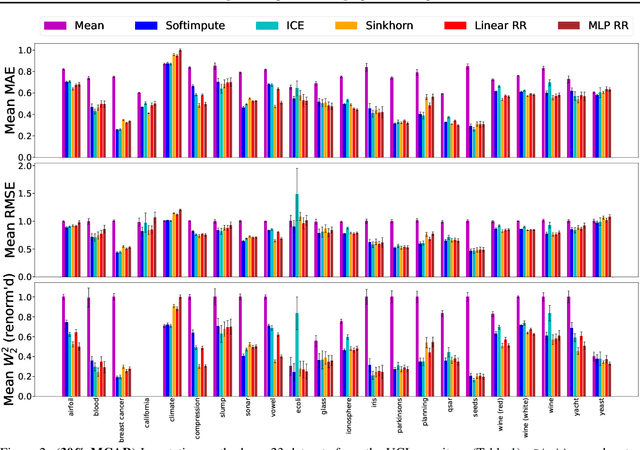
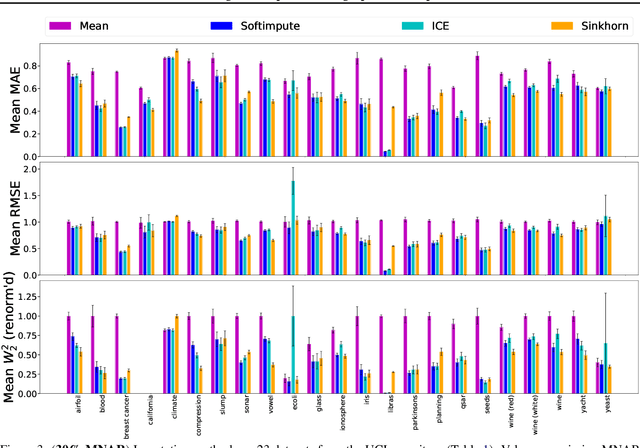
Missing Data Imputation using Optimal Transport

Missing data is a crucial issue when applying machine learning algorithms to real-world datasets. Starting from the simple assumption that two batches extracted randomly from the same dataset should share the same distribution, we leverage optimal transport distances to quantify that criterion and turn it into a loss function to impute missing data values. We propose practical methods to minimize these losses using end-to-end learning, that can exploit or not parametric assumptions on the underlying distributions of values. We evaluate our methods on datasets from the UCI repository, in MCAR, MAR and MNAR settings. These experiments show that OT-based methods match or out-perform state-of-the-art imputation methods, even for high percentages of missing values.

Subspace Detours: Building Transport Plans that are Optimal on Subspace Projections

Sliced Wasserstein metrics between probability measures solve the optimal transport (OT) problem on univariate projections, and average such maps across projections. The recent interest for the SW distance shows that much can be gained by looking at optimal maps between measures in smaller subspaces, as opposed to the curse-of-dimensionality price one has to pay in higher dimensions. Any transport estimated in a subspace remains, however, an object that can only be used in that subspace. We propose in this work two methods to extrapolate, from an transport map that is optimal on a subspace, one that is nearly optimal in the entire space. We prove that the best optimal transport plan that takes such "subspace detours" is a generalization of the Knothe-Rosenblatt transport. We show that these plans can be explicitly formulated when comparing Gaussians measures (between which the Wasserstein distance is usually referred to as the Bures or Fr\'echet distance). Building from there, we provide an algorithm to select optimal subspaces given pairs of Gaussian measures, and study scenarios in which that mediating subspace can be selected using prior information. We consider applications to NLP and evaluation of image quality (FID scores).

Generalizing Point Embeddings using the Wasserstein Space of Elliptical Distributions

Embedding complex objects as vectors in low dimensional spaces is a longstanding problem in machine learning. We propose in this work an extension of that approach, which consists in embedding objects as elliptical probability distributions, namely distributions whose densities have elliptical level sets. We endow these measures with the 2-Wasserstein metric, with two important benefits: (i) For such measures, the squared 2-Wasserstein metric has a closed form, equal to a weighted sum of the squared Euclidean distance between means and the squared Bures metric between covariance matrices. The latter is a Riemannian metric between positive semi-definite matrices, which turns out to be Euclidean on a suitable factor representation of such matrices, which is valid on the entire geodesic between these matrices. (ii) The 2-Wasserstein distance boils down to the usual Euclidean metric when comparing Diracs, and therefore provides a natural framework to extend point embeddings. We show that for these reasons Wasserstein elliptical embeddings are more intuitive and yield tools that are better behaved numerically than the alternative choice of Gaussian embeddings with the Kullback-Leibler divergence. In particular, and unlike previous work based on the KL geometry, we learn elliptical distributions that are not necessarily diagonal. We demonstrate the advantages of elliptical embeddings by using them for visualization, to compute embeddings of words, and to reflect entailment or hypernymy.

Large Margin Nearest Neighbor Classification using Curved Mahalanobis Distances

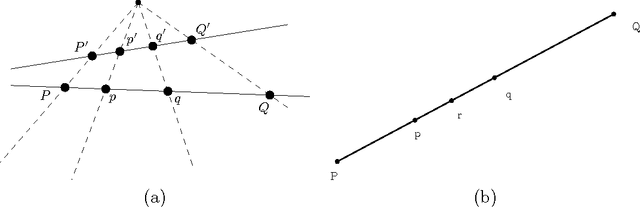
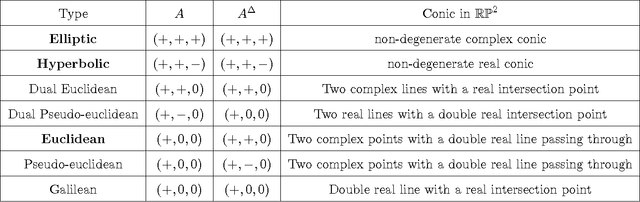
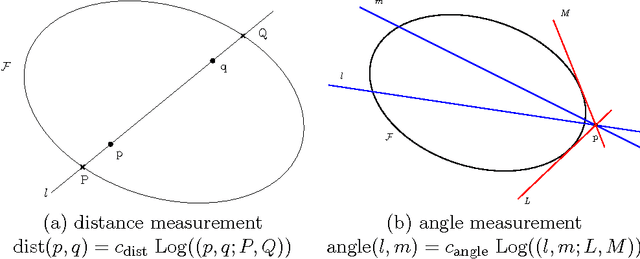
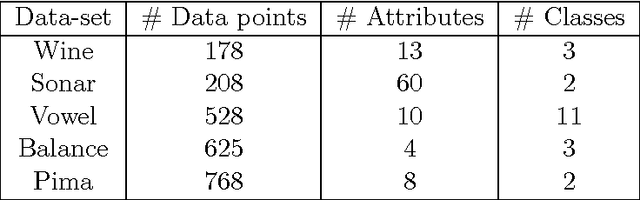
We consider the supervised classification problem of machine learning in Cayley-Klein projective geometries: We show how to learn a curved Mahalanobis metric distance corresponding to either the hyperbolic geometry or the elliptic geometry using the Large Margin Nearest Neighbor (LMNN) framework. We report on our experimental results, and further consider the case of learning a mixed curved Mahalanobis distance. Besides, we show that the Cayley-Klein Voronoi diagrams are affine, and can be built from an equivalent (clipped) power diagrams, and that Cayley-Klein balls have Mahalanobis shapes with displaced centers.