Learning Vortex Dynamics for Fluid Inference and Prediction

We propose a novel differentiable vortex particle (DVP) method to infer and predict fluid dynamics from a single video. Lying at its core is a particle-based latent space to encapsulate the hidden, Lagrangian vortical evolution underpinning the observable, Eulerian flow phenomena. Our differentiable vortex particles are coupled with a learnable, vortex-to-velocity dynamics mapping to effectively capture the complex flow features in a physically-constrained, low-dimensional space. This representation facilitates the learning of a fluid simulator tailored to the input video that can deliver robust, long-term future predictions. The value of our method is twofold: first, our learned simulator enables the inference of hidden physics quantities (e.g., velocity field) purely from visual observation; secondly, it also supports future prediction, constructing the input video's sequel along with its future dynamics evolution. We compare our method with a range of existing methods on both synthetic and real-world videos, demonstrating improved reconstruction quality, visual plausibility, and physical integrity.

Policy Transfer via Enhanced Action Space

Though transfer learning is promising to increase the learning efficiency, the existing methods are still subject to the challenges from long-horizon tasks, especially when expert policies are sub-optimal and partially useful. Hence, a novel algorithm named EASpace (Enhanced Action Space) is proposed in this paper to transfer the knowledge of multiple sub-optimal expert policies. EASpace formulates each expert policy into multiple macro actions with different execution time period, then integrates all macro actions into the primitive action space directly. Through this formulation, the proposed EASpace could learn when to execute which expert policy and how long it lasts. An intra-macro-action learning rule is proposed by adjusting the temporal difference target of macro actions to improve the data efficiency and alleviate the non-stationarity issue in multi-agent settings. Furthermore, an additional reward proportional to the execution time of macro actions is introduced to encourage the environment exploration via macro actions, which is significant to learn a long-horizon task. Theoretical analysis is presented to show the convergence of the proposed algorithm. The efficiency of the proposed algorithm is illustrated by a grid-based game and a multi-agent pursuit problem. The proposed algorithm is also implemented to real physical systems to justify its effectiveness.

FSID: Fully Synthetic Image Denoising via Procedural Scene Generation

For low-level computer vision and image processing ML tasks, training on large datasets is critical for generalization. However, the standard practice of relying on real-world images primarily from the Internet comes with image quality, scalability, and privacy issues, especially in commercial contexts. To address this, we have developed a procedural synthetic data generation pipeline and dataset tailored to low-level vision tasks. Our Unreal engine-based synthetic data pipeline populates large scenes algorithmically with a combination of random 3D objects, materials, and geometric transformations. Then, we calibrate the camera noise profiles to synthesize the noisy images. From this pipeline, we generated a fully synthetic image denoising dataset (FSID) which consists of 175,000 noisy/clean image pairs. We then trained and validated a CNN-based denoising model, and demonstrated that the model trained on this synthetic data alone can achieve competitive denoising results when evaluated on real-world noisy images captured with smartphone cameras.

Symplectically Integrated Symbolic Regression of Hamiltonian Dynamical Systems

Here we present Symplectically Integrated Symbolic Regression (SISR), a novel technique for learning physical governing equations from data. SISR employs a deep symbolic regression approach, using a multi-layer LSTM-RNN with mutation to probabilistically sample Hamiltonian symbolic expressions. Using symplectic neural networks, we develop a model-agnostic approach for extracting meaningful physical priors from the data that can be imposed on-the-fly into the RNN output, limiting its search space. Hamiltonians generated by the RNN are optimized and assessed using a fourth-order symplectic integration scheme; prediction performance is used to train the LSTM-RNN to generate increasingly better functions via a risk-seeking policy gradients approach. Employing these techniques, we extract correct governing equations from oscillator, pendulum, two-body, and three-body gravitational systems with noisy and extremely small datasets.

Learning Spatio-Temporal Downsampling for Effective Video Upscaling

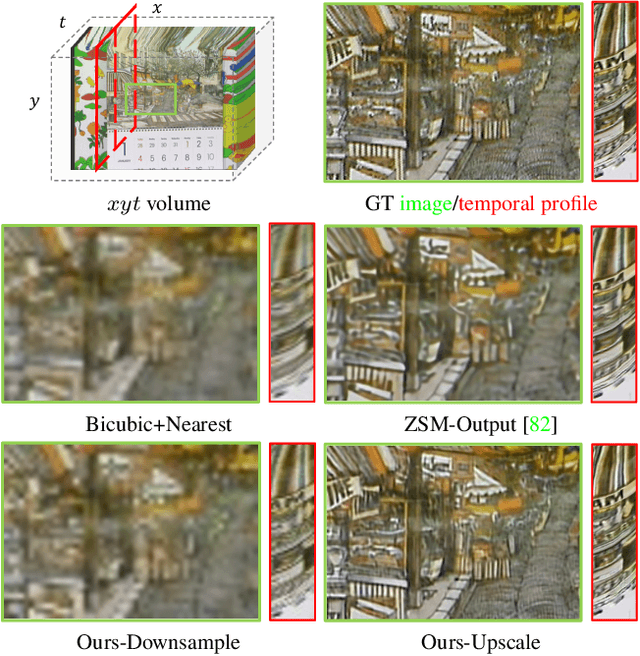
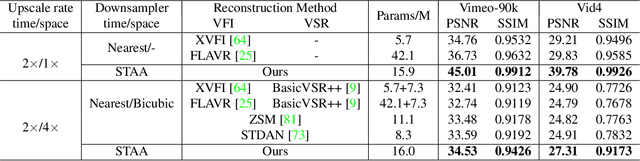
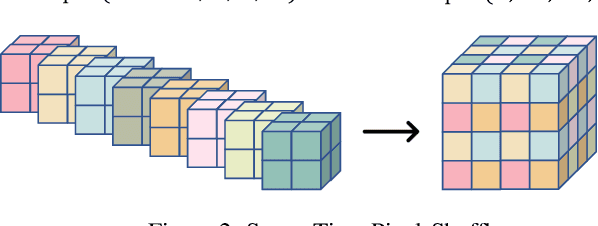
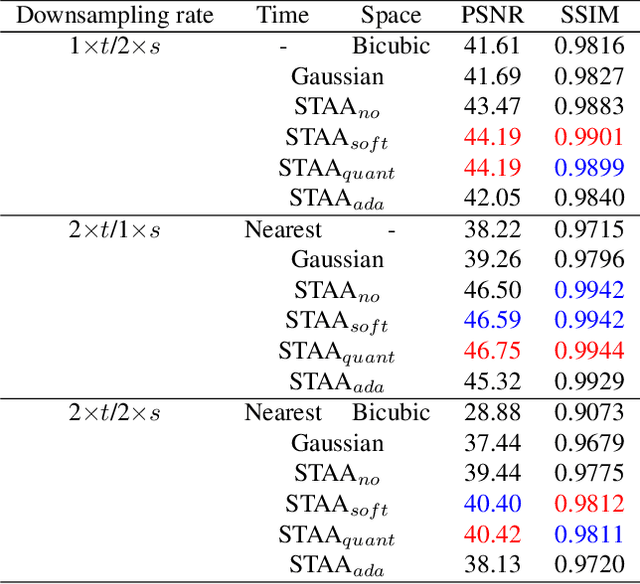
Downsampling is one of the most basic image processing operations. Improper spatio-temporal downsampling applied on videos can cause aliasing issues such as moir\'e patterns in space and the wagon-wheel effect in time. Consequently, the inverse task of upscaling a low-resolution, low frame-rate video in space and time becomes a challenging ill-posed problem due to information loss and aliasing artifacts. In this paper, we aim to solve the space-time aliasing problem by learning a spatio-temporal downsampler. Towards this goal, we propose a neural network framework that jointly learns spatio-temporal downsampling and upsampling. It enables the downsampler to retain the key patterns of the original video and maximizes the reconstruction performance of the upsampler. To make the downsamping results compatible with popular image and video storage formats, the downsampling results are encoded to uint8 with a differentiable quantization layer. To fully utilize the space-time correspondences, we propose two novel modules for explicit temporal propagation and space-time feature rearrangement. Experimental results show that our proposed method significantly boosts the space-time reconstruction quality by preserving spatial textures and motion patterns in both downsampling and upscaling. Moreover, our framework enables a variety of applications, including arbitrary video resampling, blurry frame reconstruction, and efficient video storage.

On Real-time Image Reconstruction with Neural Networks for MRI-guided Radiotherapy

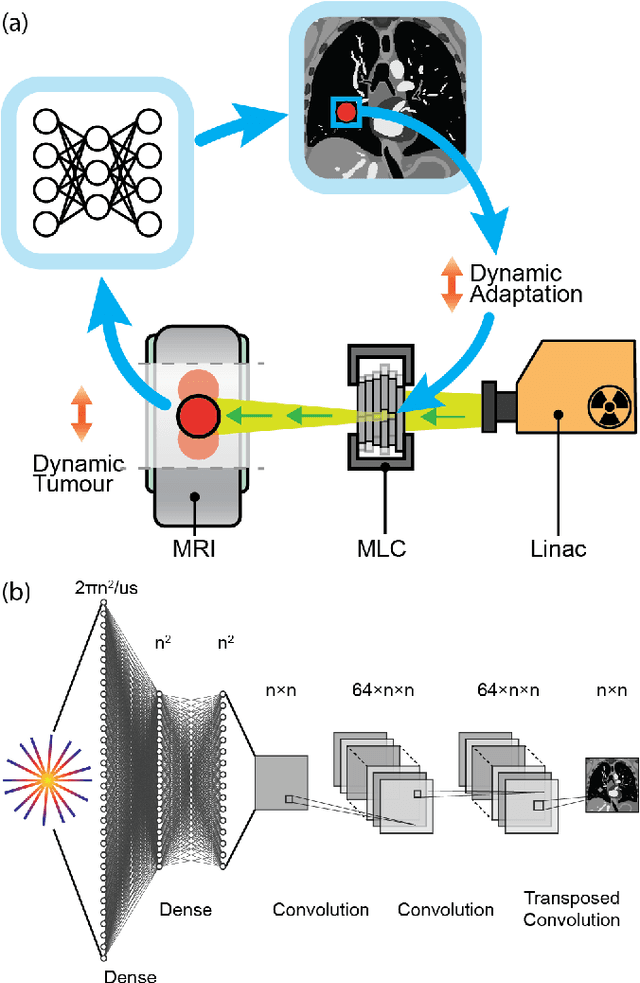
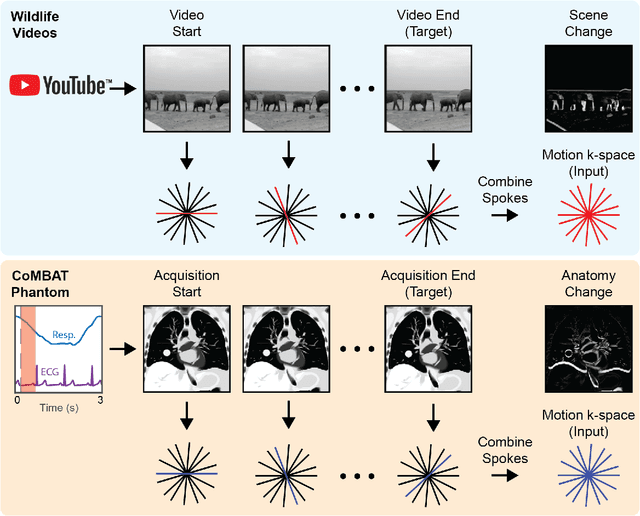
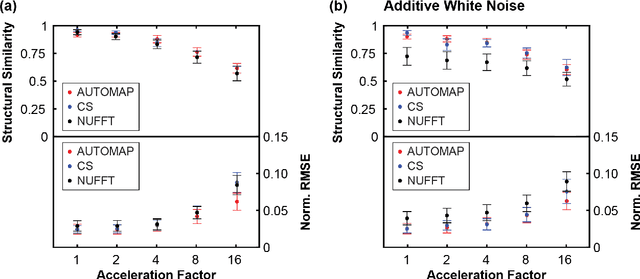
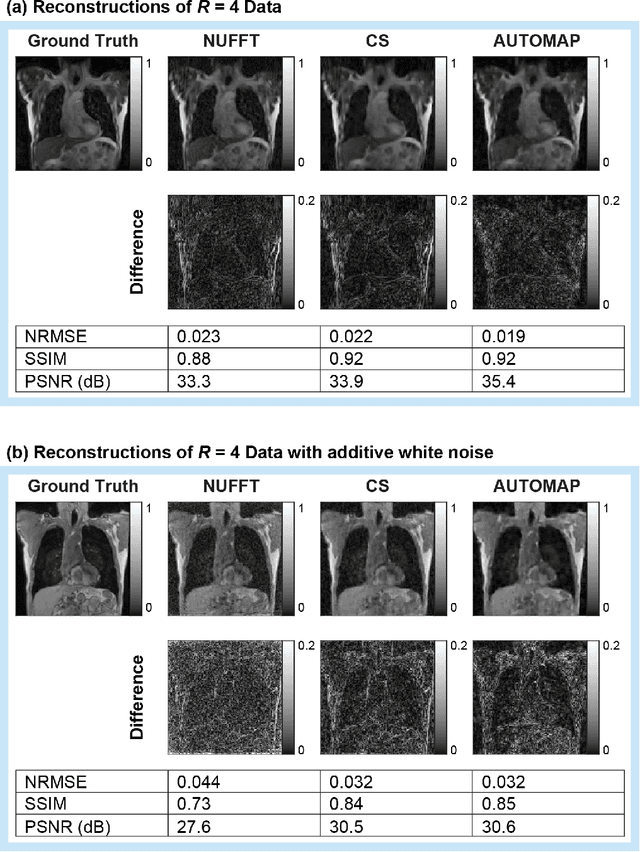
MRI-guidance techniques that dynamically adapt radiation beams to follow tumor motion in real-time will lead to more accurate cancer treatments and reduced collateral healthy tissue damage. The gold-standard for reconstruction of undersampled MR data is compressed sensing (CS) which is computationally slow and limits the rate that images can be available for real-time adaptation. Here, we demonstrate the use of automated transform by manifold approximation (AUTOMAP), a generalized framework that maps raw MR signal to the target image domain, to rapidly reconstruct images from undersampled radial k-space data. The AUTOMAP neural network was trained to reconstruct images from a golden-angle radial acquisition, a benchmark for motion-sensitive imaging, on lung cancer patient data and generic images from ImageNet. Model training was subsequently augmented with motion-encoded k-space data derived from videos in the YouTube-8M dataset to encourage motion robust reconstruction. We find that AUTOMAP-reconstructed radial k-space has equivalent accuracy to CS but with much shorter processing times after initial fine-tuning on retrospectively acquired lung cancer patient data. Validation of motion-trained models with a virtual dynamic lung tumor phantom showed that the generalized motion properties learned from YouTube lead to improved target tracking accuracy. Our work shows that AUTOMAP can achieve real-time, accurate reconstruction of radial data. These findings imply that neural-network-based reconstruction is potentially superior to existing approaches for real-time image guidance applications.

Nonseparable Symplectic Neural Networks

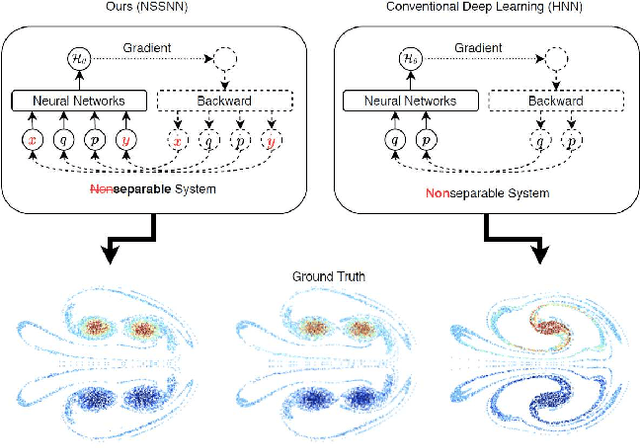
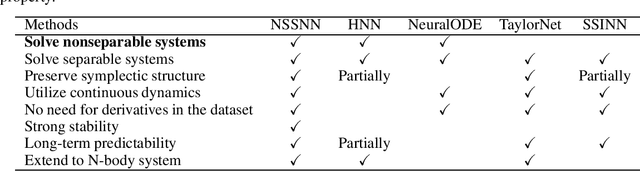
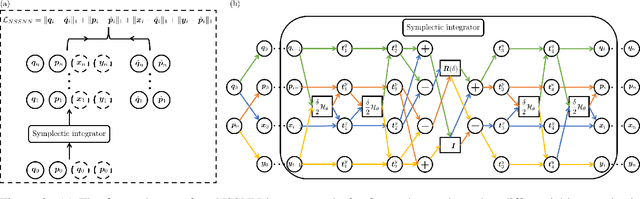
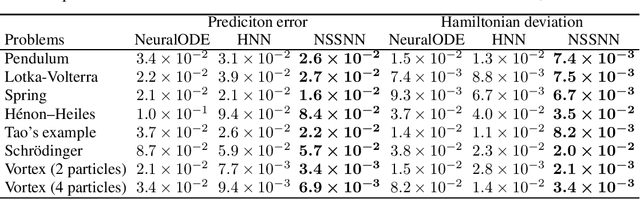
Predicting the behaviors of Hamiltonian systems has been drawing increasing attention in scientific machine learning. However, the vast majority of the literature was focused on predicting separable Hamiltonian systems with their kinematic and potential energy terms being explicitly decoupled, while building data-driven paradigms to predict nonseparable Hamiltonian systems that are ubiquitous in fluid dynamics and quantum mechanics were rarely explored. The main computational challenge lies in the effective embedding of symplectic priors to describe the inherently coupled evolution of position and momentum, which typically exhibits intricate dynamics with many degrees of freedom. To solve the problem, we propose a novel neural network architecture, Nonseparable Symplectic Neural Networks (NSSNNs), to uncover and embed the symplectic structure of a nonseparable Hamiltonian system from limited observation data. The enabling mechanics of our approach is an augmented symplectic time integrator to decouple the position and momentum energy terms and facilitate their evolution. We demonstrated the efficacy and versatility of our method by predicting a wide range of Hamiltonian systems, both separable and nonseparable, including vortical flow and quantum system. We showed the unique computational merits of our approach to yield long-term, accurate, and robust predictions for large-scale Hamiltonian systems by rigorously enforcing symplectomorphism.

Soft Multicopter Control using Neural Dynamics Identification

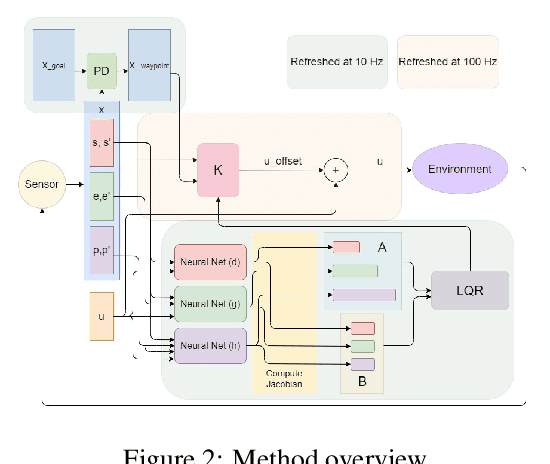
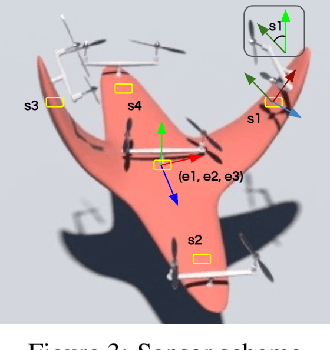
Dynamic control of a soft-body robot to deliver complex behaviors with low-dimensional actuation inputs is challenging. In this paper, we present a computational approach to automatically generate versatile, underactuated control policies that drives soft-bodied machines with complicated structures and nonlinear dynamics. Our target application is focused on the autonomous control of a soft multicopter, featured by its elastic material components, non-conventional shapes, and asymmetric rotor layouts, to precisely deliver compliant deformation and agile locomotion. The central piece of our approach lies in a lightweight neural surrogate model to identify and predict the temporal evolution of a set of geometric variables characterizing an elastic soft body. This physics-based learning model is further integrated into a Linear Quadratic Regulator (LQR) control loop enhanced by a novel online fixed-point relinearization scheme to accommodate the dynamic body balance, allowing an aggressive reduction of the computational overhead caused by the conventional full-scale sensing-simulation-control workflow. We demonstrate the efficacy of our approach by generating controllers for a broad spectrum of customized soft multicopter designs and testing them in a high-fidelity physics simulation environment. The control algorithm enables the multicopters to perform a variety of tasks, including hovering, trajectory tracking, cruising and active deforming.

Learning Physical Constraints with Neural Projections

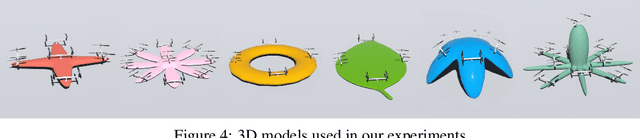
We propose a new family of neural networks to predict the behaviors of physical systems by learning their underpinning constraints. A neural projection operator liesat the heart of our approach, composed of a lightweight network with an embedded recursive architecture that interactively enforces learned underpinning constraints and predicts the various governed behaviors of different physical systems. Our neural projection operator is motivated by the position-based dynamics model that has been used widely in game and visual effects industries to unify the various fast physics simulators. Our method can automatically and effectively uncover a broad range of constraints from observation point data, such as length, angle, bending, collision, boundary effects, and their arbitrary combinations, without any connectivity priors. We provide a multi-group point representation in conjunction with a configurable network connection mechanism to incorporate prior inputs for processing complex physical systems. We demonstrated the efficacy of our approach by learning a set of challenging physical systems all in a unified and simple fashion including: rigid bodies with complex geometries, ropes with varying length and bending, articulated soft and rigid bodies, and multi-object collisions with complex boundaries.

Sparse Symplectically Integrated Neural Networks

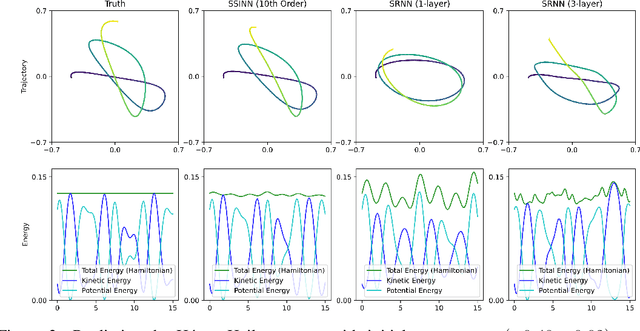
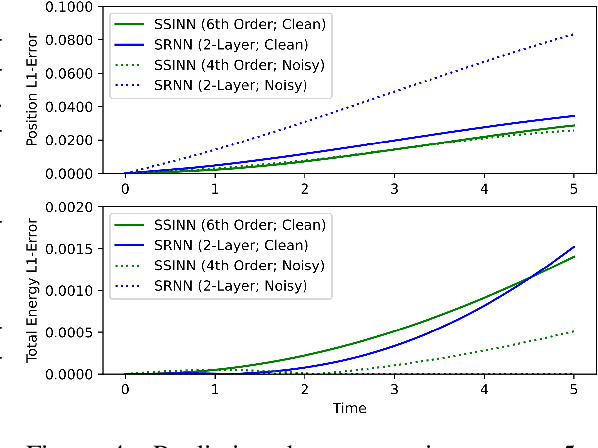
We introduce Sparse Symplectically Integrated Neural Networks (SSINNs), a novel model for learning Hamiltonian dynamical systems from data. SSINNs combine fourth-order symplectic integration with a learned parameterization of the Hamiltonian obtained using sparse regression through a mathematically elegant function space. This allows for interpretable models that incorporate symplectic inductive biases and have low memory requirements. We evaluate SSINNs on four classical Hamiltonian dynamical problems: the H\'enon-Heiles system, nonlinearly coupled oscillators, a multi-particle mass-spring system, and a pendulum system. Our results demonstrate promise in both system prediction and conservation of energy, outperforming the current state-of-the-art black-box prediction techniques by an order of magnitude. Further, SSINNs successfully converge to true governing equations from highly limited and noisy data, demonstrating potential applicability in the discovery of new physical governing equations.