W4S4: WaLRUS Meets S4 for Long-Range Sequence Modeling

State Space Models (SSMs) have emerged as powerful components for sequence modeling, enabling efficient handling of long-range dependencies via linear recurrence and convolutional computation. However, their effectiveness depends heavily on the choice and initialization of the state matrix. In this work, we build on the SaFARi framework and existing WaLRUS SSMs to introduce a new variant, W4S4 (WaLRUS for S4), a new class of SSMs constructed from redundant wavelet frames. WaLRUS admits a stable diagonalization and supports fast kernel computation without requiring low-rank approximations, making it both theoretically grounded and computationally efficient. We show that WaLRUS retains information over long horizons significantly better than HiPPO-based SSMs, both in isolation and when integrated into deep architectures such as S4. Our experiments demonstrate consistent improvements across delay reconstruction tasks, classification benchmarks, and long-range sequence modeling, confirming that high-quality, structured initialization enabled by wavelet-based state dynamic offers substantial advantages over existing alternatives. WaLRUS provides a scalable and versatile foundation for the next generation of deep SSM-based models.

WaLRUS: Wavelets for Long-range Representation Using SSMs

State-Space Models (SSMs) have proven to be powerful tools for modeling long-range dependencies in sequential data. While the recent method known as HiPPO has demonstrated strong performance, and formed the basis for machine learning models S4 and Mamba, it remains limited by its reliance on closed-form solutions for a few specific, well-behaved bases. The SaFARi framework generalized this approach, enabling the construction of SSMs from arbitrary frames, including non-orthogonal and redundant ones, thus allowing an infinite diversity of possible "species" within the SSM family. In this paper, we introduce WaLRUS (Wavelets for Long-range Representation Using SSMs), a new implementation of SaFARi built from Daubechies wavelets.

SaFARi: State-Space Models for Frame-Agnostic Representation

State-Space Models (SSMs) have re-emerged as a powerful tool for online function approximation, and as the backbone of machine learning models for long-range dependent data. However, to date, only a few polynomial bases have been explored for this purpose, and the state-of-the-art implementations were built upon the best of a few limited options. In this paper, we present a generalized method for building an SSM with any frame or basis, rather than being restricted to polynomials. This framework encompasses the approach known as HiPPO, but also permits an infinite diversity of other possible "species" within the SSM architecture. We dub this approach SaFARi: SSMs for Frame-Agnostic Representation.

Self-Consuming Generative Models Go MAD

Seismic advances in generative AI algorithms for imagery, text, and other data types has led to the temptation to use synthetic data to train next-generation models. Repeating this process creates an autophagous (self-consuming) loop whose properties are poorly understood. We conduct a thorough analytical and empirical analysis using state-of-the-art generative image models of three families of autophagous loops that differ in how fixed or fresh real training data is available through the generations of training and in whether the samples from previous generation models have been biased to trade off data quality versus diversity. Our primary conclusion across all scenarios is that without enough fresh real data in each generation of an autophagous loop, future generative models are doomed to have their quality (precision) or diversity (recall) progressively decrease. We term this condition Model Autophagy Disorder (MAD), making analogy to mad cow disease.

TITAN: Bringing The Deep Image Prior to Implicit Representations

We study the interpolation capabilities of implicit neural representations (INRs) of images. In principle, INRs promise a number of advantages, such as continuous derivatives and arbitrary sampling, being freed from the restrictions of a raster grid. However, empirically, INRs have been observed to poorly interpolate between the pixels of the fit image; in other words, they do not inherently possess a suitable prior for natural images. In this paper, we propose to address and improve INRs' interpolation capabilities by explicitly integrating image prior information into the INR architecture via deep decoder, a specific implementation of the deep image prior (DIP). Our method, which we call TITAN, leverages a residual connection from the input which enables integrating the principles of the grid-based DIP into the grid-free INR. Through super-resolution and computed tomography experiments, we demonstrate that our method significantly improves upon classic INRs, thanks to the induced natural image bias. We also find that by constraining the weights to be sparse, image quality and sharpness are enhanced, increasing the Lipschitz constant.

NFT-K: Non-Fungible Tangent Kernels

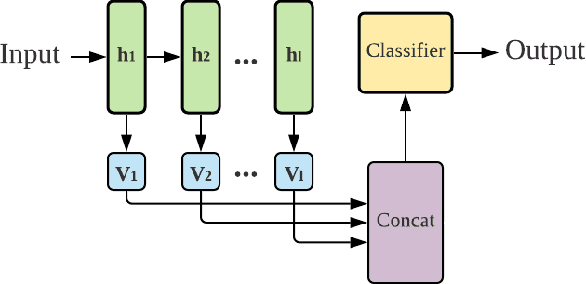
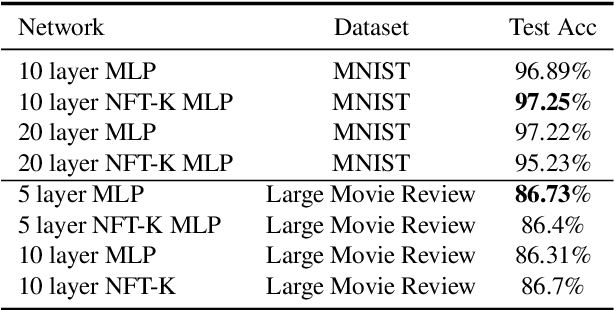
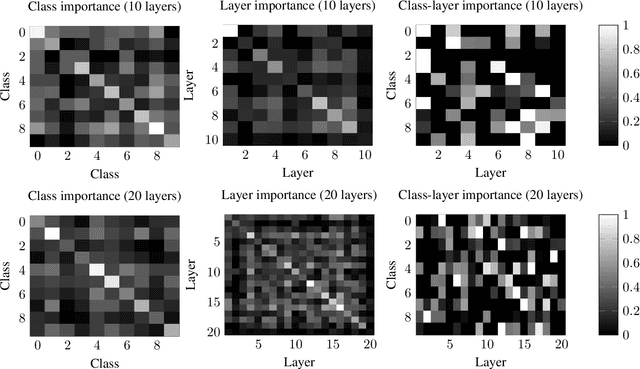
Deep neural networks have become essential for numerous applications due to their strong empirical performance such as vision, RL, and classification. Unfortunately, these networks are quite difficult to interpret, and this limits their applicability in settings where interpretability is important for safety, such as medical imaging. One type of deep neural network is neural tangent kernel that is similar to a kernel machine that provides some aspect of interpretability. To further contribute interpretability with respect to classification and the layers, we develop a new network as a combination of multiple neural tangent kernels, one to model each layer of the deep neural network individually as opposed to past work which attempts to represent the entire network via a single neural tangent kernel. We demonstrate the interpretability of this model on two datasets, showing that the multiple kernels model elucidates the interplay between the layers and predictions.

Wearing a MASK: Compressed Representations of Variable-Length Sequences Using Recurrent Neural Tangent Kernels

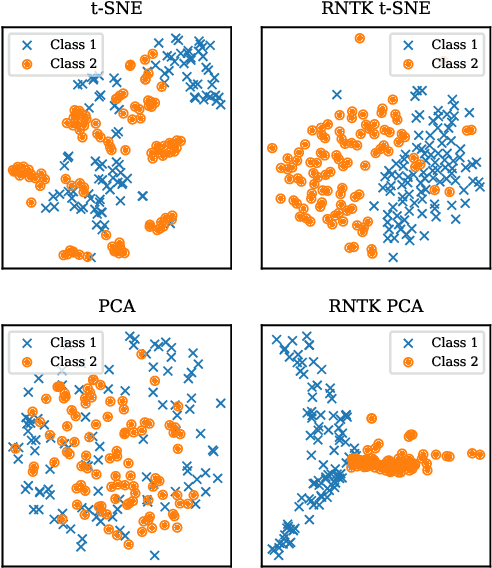
High dimensionality poses many challenges to the use of data, from visualization and interpretation, to prediction and storage for historical preservation. Techniques abound to reduce the dimensionality of fixed-length sequences, yet these methods rarely generalize to variable-length sequences. To address this gap, we extend existing methods that rely on the use of kernels to variable-length sequences via use of the Recurrent Neural Tangent Kernel (RNTK). Since a deep neural network with ReLu activation is a Max-Affine Spline Operator (MASO), we dub our approach Max-Affine Spline Kernel (MASK). We demonstrate how MASK can be used to extend principal components analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE) and apply these new algorithms to separate synthetic time series data sampled from second-order differential equations.