LPLgrad: Optimizing Active Learning Through Gradient Norm Sample Selection and Auxiliary Model Training

Machine learning models are increasingly being utilized across various fields and tasks due to their outstanding performance and strong generalization capabilities. Nonetheless, their success hinges on the availability of large volumes of annotated data, the creation of which is often labor-intensive, time-consuming, and expensive. Many active learning (AL) approaches have been proposed to address these challenges, but they often fail to fully leverage the information from the core phases of AL, such as training on the labeled set and querying new unlabeled samples. To bridge this gap, we propose a novel AL approach, Loss Prediction Loss with Gradient Norm (LPLgrad), designed to quantify model uncertainty effectively and improve the accuracy of image classification tasks. LPLgrad operates in two distinct phases: (i) {\em Training Phase} aims to predict the loss for input features by jointly training a main model and an auxiliary model. Both models are trained on the labeled data to maximize the efficiency of the learning process, an aspect often overlooked in previous AL methods. This dual-model approach enhances the ability to extract complex input features and learn intrinsic patterns from the data effectively; (ii) {\em Querying Phase} that quantifies the uncertainty of the main model to guide sample selection. This is achieved by calculating the gradient norm of the entropy values for samples in the unlabeled dataset. Samples with the highest gradient norms are prioritized for labeling and subsequently added to the labeled set, improving the model's performance with minimal labeling effort. Extensive evaluations on real-world datasets demonstrate that the LPLgrad approach outperforms state-of-the-art methods by order of magnitude in terms of accuracy on a small number of labeled images, yet achieving comparable training and querying times in multiple image classification tasks.

FisherMask: Enhancing Neural Network Labeling Efficiency in Image Classification Using Fisher Information

Deep learning (DL) models are popular across various domains due to their remarkable performance and efficiency. However, their effectiveness relies heavily on large amounts of labeled data, which are often time-consuming and labor-intensive to generate manually. To overcome this challenge, it is essential to develop strategies that reduce reliance on extensive labeled data while preserving model performance. In this paper, we propose FisherMask, a Fisher information-based active learning (AL) approach that identifies key network parameters by masking them based on their Fisher information values. FisherMask enhances batch AL by using Fisher information to select the most critical parameters, allowing the identification of the most impactful samples during AL training. Moreover, Fisher information possesses favorable statistical properties, offering valuable insights into model behavior and providing a better understanding of the performance characteristics within the AL pipeline. Our extensive experiments demonstrate that FisherMask significantly outperforms state-of-the-art methods on diverse datasets, including CIFAR-10 and FashionMNIST, especially under imbalanced settings. These improvements lead to substantial gains in labeling efficiency. Hence serving as an effective tool to measure the sensitivity of model parameters to data samples. Our code is available on \url{https://github.com/sgchr273/FisherMask}.

Addressing Data Heterogeneity in Federated Learning of Cox Proportional Hazards Models

The diversity in disease profiles and therapeutic approaches between hospitals and health professionals underscores the need for patient-centric personalized strategies in healthcare. Alongside this, similarities in disease progression across patients can be utilized to improve prediction models in survival analysis. The need for patient privacy and the utility of prediction models can be simultaneously addressed in the framework of Federated Learning (FL). This paper outlines an approach in the domain of federated survival analysis, specifically the Cox Proportional Hazards (CoxPH) model, with a specific focus on mitigating data heterogeneity and elevating model performance. We present an FL approach that employs feature-based clustering to enhance model accuracy across synthetic datasets and real-world applications, including the Surveillance, Epidemiology, and End Results (SEER) database. Furthermore, we consider an event-based reporting strategy that provides a dynamic approach to model adaptation by responding to local data changes. Our experiments show the efficacy of our approach and discuss future directions for a practical application of FL in healthcare.

Using Geographic Location-based Public Health Features in Survival Analysis

Time elapsed till an event of interest is often modeled using the survival analysis methodology, which estimates a survival score based on the input features. There is a resurgence of interest in developing more accurate prediction models for time-to-event prediction in personalized healthcare using modern tools such as neural networks. Higher quality features and more frequent observations improve the predictions for a patient, however, the impact of including a patient's geographic location-based public health statistics on individual predictions has not been studied. This paper proposes a complementary improvement to survival analysis models by incorporating public health statistics in the input features. We show that including geographic location-based public health information results in a statistically significant improvement in the concordance index evaluated on the Surveillance, Epidemiology, and End Results (SEER) dataset containing nationwide cancer incidence data. The improvement holds for both the standard Cox proportional hazards model and the state-of-the-art Deep Survival Machines model. Our results indicate the utility of geographic location-based public health features in survival analysis.

Nearest Neighbor Search Under Uncertainty

Nearest Neighbor Search (NNS) is a central task in knowledge representation, learning, and reasoning. There is vast literature on efficient algorithms for constructing data structures and performing exact and approximate NNS. This paper studies NNS under Uncertainty (NNSU). Specifically, consider the setting in which an NNS algorithm has access only to a stochastic distance oracle that provides a noisy, unbiased estimate of the distance between any pair of points, rather than the exact distance. This models many situations of practical importance, including NNS based on human similarity judgements, physical measurements, or fast, randomized approximations to exact distances. A naive approach to NNSU could employ any standard NNS algorithm and repeatedly query and average results from the stochastic oracle (to reduce noise) whenever it needs a pairwise distance. The problem is that a sufficient number of repeated queries is unknown in advance; e.g., a point maybe distant from all but one other point (crude distance estimates suffice) or it may be close to a large number of other points (accurate estimates are necessary). This paper shows how ideas from cover trees and multi-armed bandits can be leveraged to develop an NNSU algorithm that has optimal dependence on the dataset size and the (unknown)geometry of the dataset.

Generalized Chernoff Sampling for Active Learning and Structured Bandit Algorithms

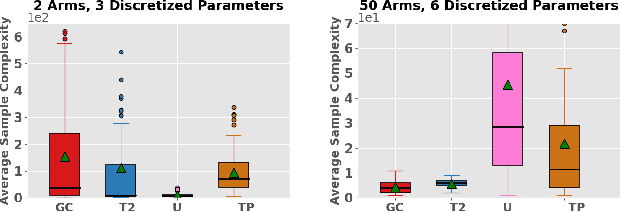
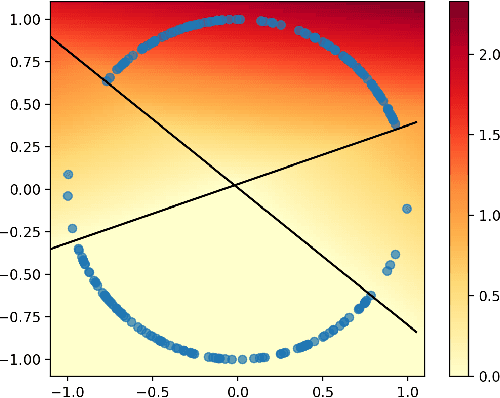
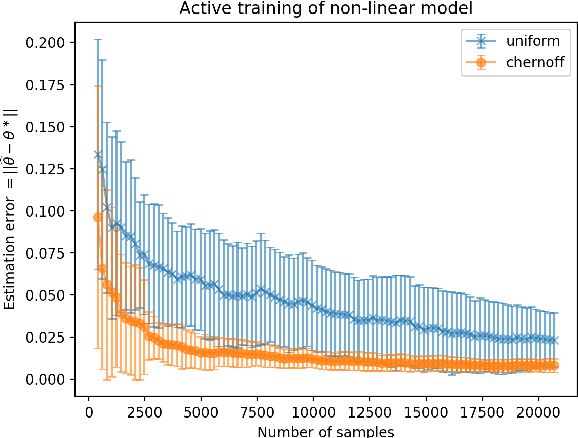
Active learning and structured stochastic bandit problems are intimately related to the classical problem of sequential experimental design. This paper studies active learning and best-arm identification in structured bandit settings from the viewpoint of active sequential hypothesis testing, a framework initiated by Chernoff (1959). We first characterize the sample complexity of Chernoff's original procedure by uncovering terms that reduce in significance as the allowed error probability $\delta \rightarrow 0$, but are nevertheless relevant at any fixed value of $\delta > 0$. While initially proposed for testing among finitely many hypotheses, we obtain the analogue of Chernoff sampling for the case when the hypotheses belong to a compact space. This makes it applicable to active learning and structured bandit problems, where the unknown parameter specifying the arm means is often assumed to be an element of Euclidean space. Empirically, we demonstrate the potential of our proposed approach for active learning of neural network models and in the linear bandit setting, where we observe that our general-purpose approach compares favorably to state-of-the-art methods.

Finding All ε-Good Arms in Stochastic Bandits

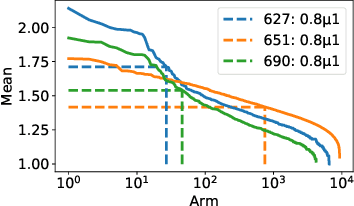
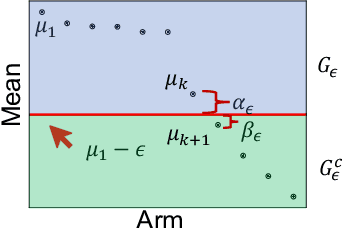
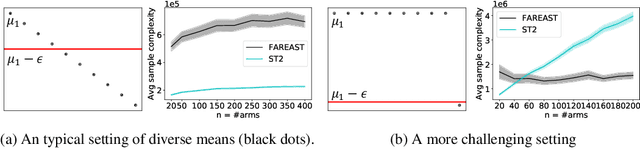
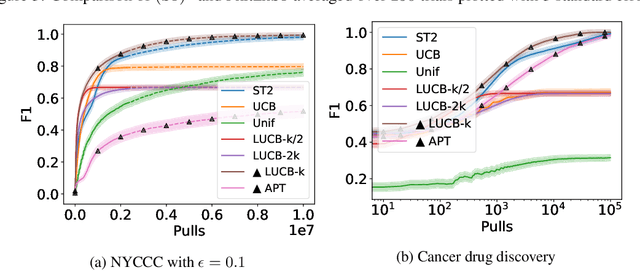
The pure-exploration problem in stochastic multi-armed bandits aims to find one or more arms with the largest (or near largest) means. Examples include finding an {\epsilon}-good arm, best-arm identification, top-k arm identification, and finding all arms with means above a specified threshold. However, the problem of finding all {\epsilon}-good arms has been overlooked in past work, although arguably this may be the most natural objective in many applications. For example, a virologist may conduct preliminary laboratory experiments on a large candidate set of treatments and move all {\epsilon}-good treatments into more expensive clinical trials. Since the ultimate clinical efficacy is uncertain, it is important to identify all {\epsilon}-good candidates. Mathematically, the all-{\epsilon}-good arm identification problem presents significant new challenges and surprises that do not arise in the pure-exploration objectives studied in the past. We introduce two algorithms to overcome these and demonstrate their great empirical performance on a large-scale crowd-sourced dataset of 2.2M ratings collected by the New Yorker Caption Contest as well as a dataset testing hundreds of possible cancer drugs.

Optimal Confidence Regions for the Multinomial Parameter

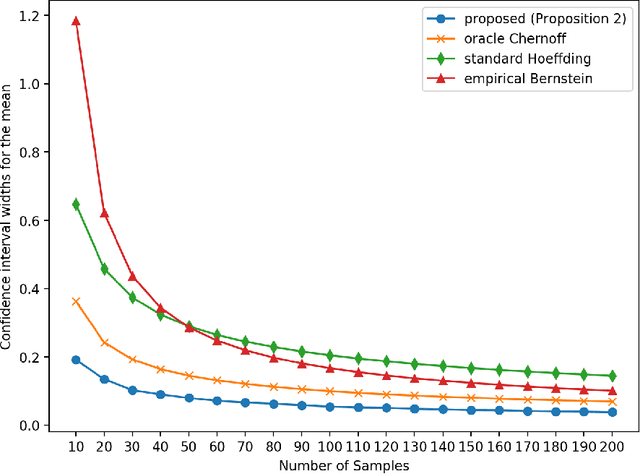
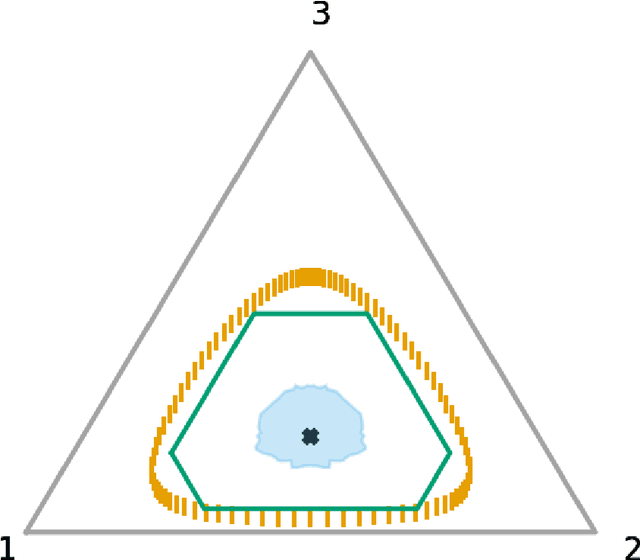
Construction of tight confidence regions and intervals is central to statistical inference and decision-making. Consider an empirical distribution $\widehat{\boldsymbol{p}}$ generated from $n$ iid realizations of a random variable that takes one of $k$ possible values according to an unknown distribution $\boldsymbol{p}$. This is analogous with a single draw from a multinomial distribution. A confidence region is a subset of the probability simplex that depends on $\widehat{\boldsymbol{p}}$ and contains the unknown $\boldsymbol{p}$ with a specified confidence. This paper shows how one can construct minimum average volume confidence regions, answering a long standing question. We also show the optimality of the regions directly translates to optimal confidence intervals of functionals, such as the mean, variance and median.

MaxGap Bandit: Adaptive Algorithms for Approximate Ranking

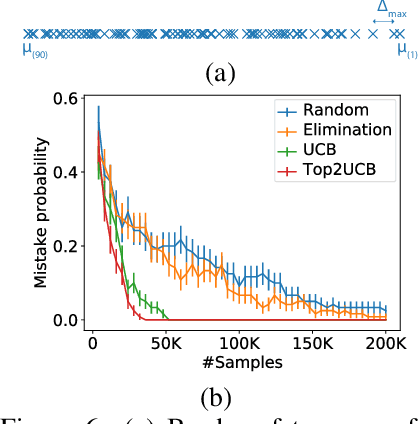
This paper studies the problem of adaptively sampling from K distributions (arms) in order to identify the largest gap between any two adjacent means. We call this the MaxGap-bandit problem. This problem arises naturally in approximate ranking, noisy sorting, outlier detection, and top-arm identification in bandits. The key novelty of the MaxGap-bandit problem is that it aims to adaptively determine the natural partitioning of the distributions into a subset with larger means and a subset with smaller means, where the split is determined by the largest gap rather than a pre-specified rank or threshold. Estimating an arm's gap requires sampling its neighboring arms in addition to itself, and this dependence results in a novel hardness parameter that characterizes the sample complexity of the problem. We propose elimination and UCB-style algorithms and show that they are minimax optimal. Our experiments show that the UCB-style algorithms require 6-8x fewer samples than non-adaptive sampling to achieve the same error.

Learning Nearest Neighbor Graphs from Noisy Distance Samples

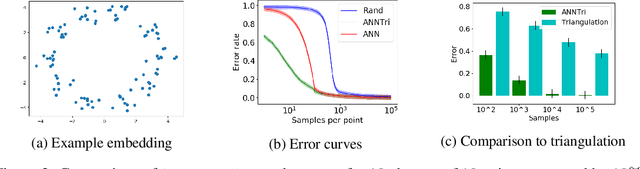
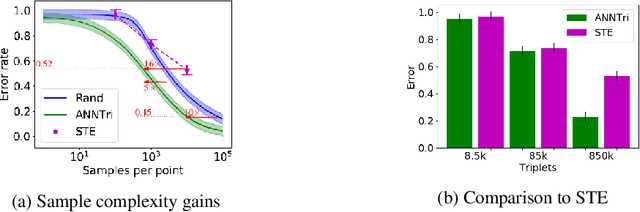
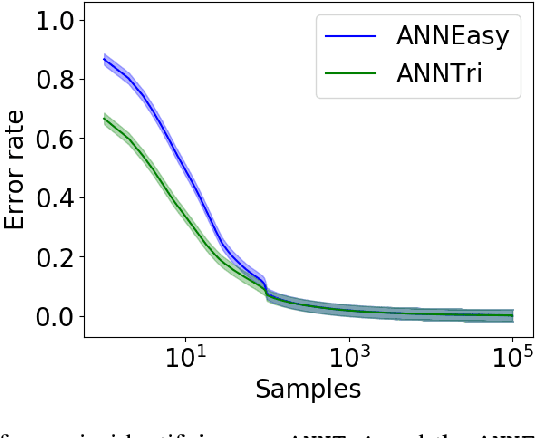
We consider the problem of learning the nearest neighbor graph of a dataset of n items. The metric is unknown, but we can query an oracle to obtain a noisy estimate of the distance between any pair of items. This framework applies to problem domains where one wants to learn people's preferences from responses commonly modeled as noisy distance judgments. In this paper, we propose an active algorithm to find the graph with high probability and analyze its query complexity. In contrast to existing work that forces Euclidean structure, our method is valid for general metrics, assuming only symmetry and the triangle inequality. Furthermore, we demonstrate efficiency of our method empirically and theoretically, needing only O(n log(n)Delta^-2) queries in favorable settings, where Delta^-2 accounts for the effect of noise. Using crowd-sourced data collected for a subset of the UT Zappos50K dataset, we apply our algorithm to learn which shoes people believe are most similar and show that it beats both an active baseline and ordinal embedding.