Blake A. Richards
The challenge of hidden gifts in multi-agent reinforcement learning
May 29, 2025Abstract:Sometimes we benefit from actions that others have taken even when we are unaware that they took those actions. For example, if your neighbor chooses not to take a parking spot in front of your house when you are not there, you can benefit, even without being aware that they took this action. These "hidden gifts" represent an interesting challenge for multi-agent reinforcement learning (MARL), since assigning credit when the beneficial actions of others are hidden is non-trivial. Here, we study the impact of hidden gifts with a very simple MARL task. In this task, agents in a grid-world environment have individual doors to unlock in order to obtain individual rewards. As well, if all the agents unlock their door the group receives a larger collective reward. However, there is only one key for all of the doors, such that the collective reward can only be obtained when the agents drop the key for others after they use it. Notably, there is nothing to indicate to an agent that the other agents have dropped the key, thus the act of dropping the key for others is a "hidden gift". We show that several different state-of-the-art RL algorithms, including MARL algorithms, fail to learn how to obtain the collective reward in this simple task. Interestingly, we find that independent model-free policy gradient agents can solve the task when we provide them with information about their own action history, but MARL agents still cannot solve the task with action history. Finally, we derive a correction term for these independent agents, inspired by learning aware approaches, which reduces the variance in learning and helps them to converge to collective success more reliably. These results show that credit assignment in multi-agent settings can be particularly challenging in the presence of "hidden gifts", and demonstrate that learning awareness in independent agents can benefit these settings.
Sufficient conditions for offline reactivation in recurrent neural networks
May 22, 2025Abstract:During periods of quiescence, such as sleep, neural activity in many brain circuits resembles that observed during periods of task engagement. However, the precise conditions under which task-optimized networks can autonomously reactivate the same network states responsible for online behavior is poorly understood. In this study, we develop a mathematical framework that outlines sufficient conditions for the emergence of neural reactivation in circuits that encode features of smoothly varying stimuli. We demonstrate mathematically that noisy recurrent networks optimized to track environmental state variables using change-based sensory information naturally develop denoising dynamics, which, in the absence of input, cause the network to revisit state configurations observed during periods of online activity. We validate our findings using numerical experiments on two canonical neuroscience tasks: spatial position estimation based on self-motion cues, and head direction estimation based on angular velocity cues. Overall, our work provides theoretical support for modeling offline reactivation as an emergent consequence of task optimization in noisy neural circuits.
* ICLR 2024
Language Agents Mirror Human Causal Reasoning Biases. How Can We Help Them Think Like Scientists?
May 14, 2025Abstract:Language model (LM) agents are increasingly used as autonomous decision-makers who need to actively gather information to guide their decisions. A crucial cognitive skill for such agents is the efficient exploration and understanding of the causal structure of the world -- key to robust, scientifically grounded reasoning. Yet, it remains unclear whether LMs possess this capability or exhibit systematic biases leading to erroneous conclusions. In this work, we examine LMs' ability to explore and infer causal relationships, using the well-established "Blicket Test" paradigm from developmental psychology. We find that LMs reliably infer the common, intuitive disjunctive causal relationships but systematically struggle with the unusual, yet equally (or sometimes even more) evidenced conjunctive ones. This "disjunctive bias" persists across model families, sizes, and prompting strategies, and performance further declines as task complexity increases. Interestingly, an analogous bias appears in human adults, suggesting that LMs may have inherited deep-seated reasoning heuristics from their training data. To this end, we quantify similarities between LMs and humans, finding that LMs exhibit adult-like inference profiles (but not children-like). Finally, we propose a test-time sampling method which explicitly samples and eliminates hypotheses about causal relationships from the LM. This scalable approach significantly reduces the disjunctive bias and moves LMs closer to the goal of scientific, causally rigorous reasoning.
Learning Successor Features the Simple Way
Oct 29, 2024



Abstract:In Deep Reinforcement Learning (RL), it is a challenge to learn representations that do not exhibit catastrophic forgetting or interference in non-stationary environments. Successor Features (SFs) offer a potential solution to this challenge. However, canonical techniques for learning SFs from pixel-level observations often lead to representation collapse, wherein representations degenerate and fail to capture meaningful variations in the data. More recent methods for learning SFs can avoid representation collapse, but they often involve complex losses and multiple learning phases, reducing their efficiency. We introduce a novel, simple method for learning SFs directly from pixels. Our approach uses a combination of a Temporal-difference (TD) loss and a reward prediction loss, which together capture the basic mathematical definition of SFs. We show that our approach matches or outperforms existing SF learning techniques in both 2D (Minigrid), 3D (Miniworld) mazes and Mujoco, for both single and continual learning scenarios. As well, our technique is efficient, and can reach higher levels of performance in less time than other approaches. Our work provides a new, streamlined technique for learning SFs directly from pixel observations, with no pretraining required.
Beyond accuracy: generalization properties of bio-plausible temporal credit assignment rules
Jun 02, 2022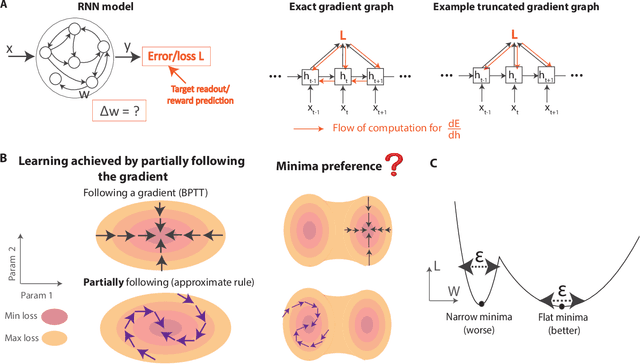
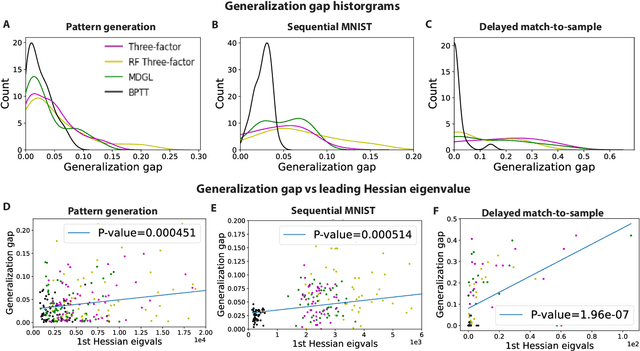
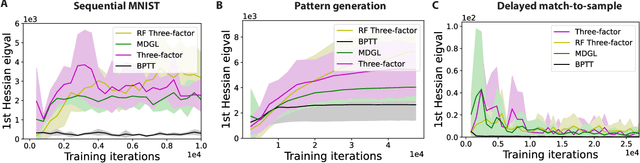
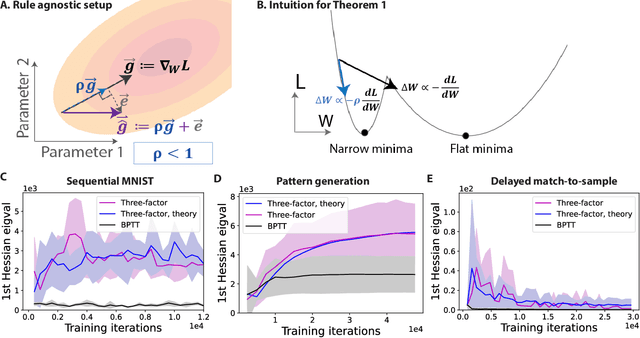
Abstract:To unveil how the brain learns, ongoing work seeks biologically-plausible approximations of gradient descent algorithms for training recurrent neural networks (RNNs). Yet, beyond task accuracy, it is unclear if such learning rules converge to solutions that exhibit different levels of generalization than their nonbiologically-plausible counterparts. Leveraging results from deep learning theory based on loss landscape curvature, we ask: how do biologically-plausible gradient approximations affect generalization? We first demonstrate that state-of-the-art biologically-plausible learning rules for training RNNs exhibit worse and more variable generalization performance compared to their machine learning counterparts that follow the true gradient more closely. Next, we verify that such generalization performance is correlated significantly with loss landscape curvature, and we show that biologically-plausible learning rules tend to approach high-curvature regions in synaptic weight space. Using tools from dynamical systems, we derive theoretical arguments and present a theorem explaining this phenomenon. This predicts our numerical results, and explains why biologically-plausible rules lead to worse and more variable generalization properties. Finally, we suggest potential remedies that could be used by the brain to mitigate this effect. To our knowledge, our analysis is the first to identify the reason for this generalization gap between artificial and biologically-plausible learning rules, which can help guide future investigations into how the brain learns solutions that generalize.
A Generalized Bootstrap Target for Value-Learning, Efficiently Combining Value and Feature Predictions
Jan 05, 2022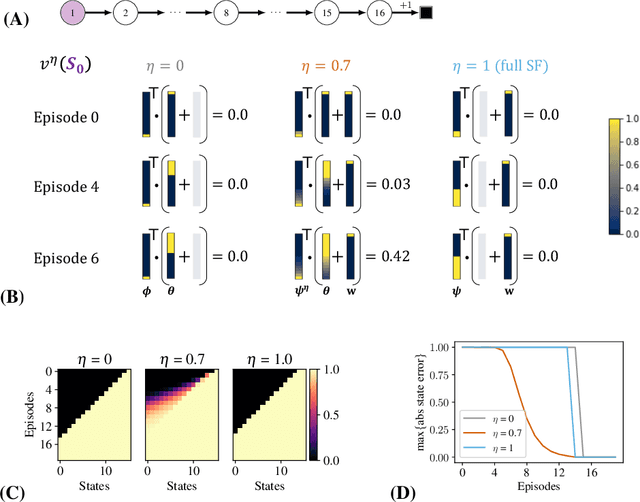

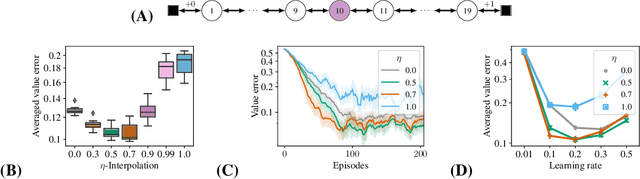
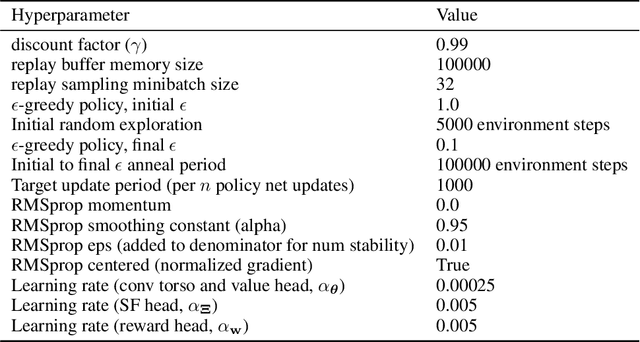
Abstract:Estimating value functions is a core component of reinforcement learning algorithms. Temporal difference (TD) learning algorithms use bootstrapping, i.e. they update the value function toward a learning target using value estimates at subsequent time-steps. Alternatively, the value function can be updated toward a learning target constructed by separately predicting successor features (SF)--a policy-dependent model--and linearly combining them with instantaneous rewards. We focus on bootstrapping targets used when estimating value functions, and propose a new backup target, the $\eta$-return mixture, which implicitly combines value-predictive knowledge (used by TD methods) with (successor) feature-predictive knowledge--with a parameter $\eta$ capturing how much to rely on each. We illustrate that incorporating predictive knowledge through an $\eta\gamma$-discounted SF model makes more efficient use of sampled experience, compared to either extreme, i.e. bootstrapping entirely on the value function estimate, or bootstrapping on the product of separately estimated successor features and instantaneous reward models. We empirically show this approach leads to faster policy evaluation and better control performance, for tabular and nonlinear function approximations, indicating scalability and generality.
CCN GAC Workshop: Issues with learning in biological recurrent neural networks
May 12, 2021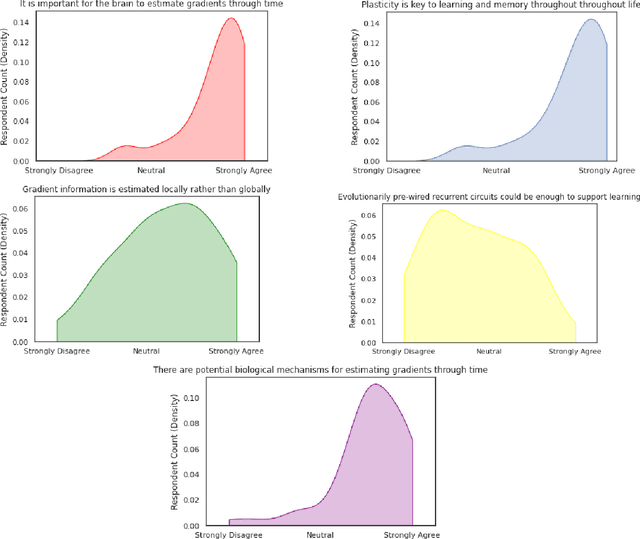
Abstract:This perspective piece came about through the Generative Adversarial Collaboration (GAC) series of workshops organized by the Computational Cognitive Neuroscience (CCN) conference in 2020. We brought together a number of experts from the field of theoretical neuroscience to debate emerging issues in our understanding of how learning is implemented in biological recurrent neural networks. Here, we will give a brief review of the common assumptions about biological learning and the corresponding findings from experimental neuroscience and contrast them with the efficiency of gradient-based learning in recurrent neural networks commonly used in artificial intelligence. We will then outline the key issues discussed in the workshop: synaptic plasticity, neural circuits, theory-experiment divide, and objective functions. Finally, we conclude with recommendations for both theoretical and experimental neuroscientists when designing new studies that could help to bring clarity to these issues.
Spike-based causal inference for weight alignment
Oct 03, 2019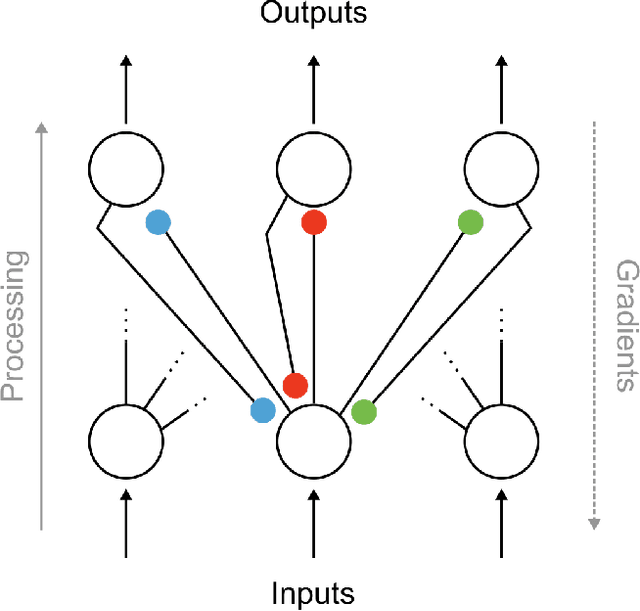

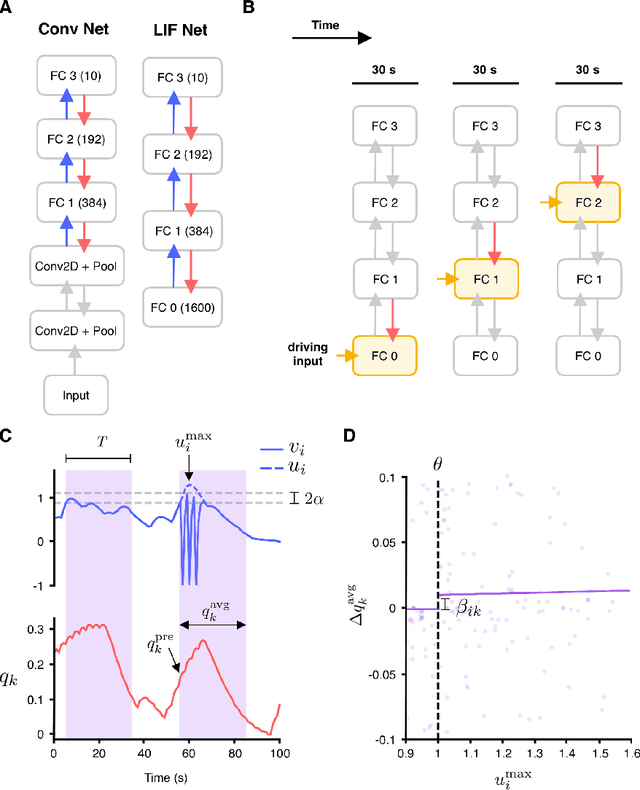
Abstract:In artificial neural networks trained with gradient descent, the weights used for processing stimuli are also used during backward passes to calculate gradients. For the real brain to approximate gradients, gradient information would have to be propagated separately, such that one set of synaptic weights is used for processing and another set is used for backward passes. This produces the so-called "weight transport problem" for biological models of learning, where the backward weights used to calculate gradients need to mirror the forward weights used to process stimuli. This weight transport problem has been considered so hard that popular proposals for biological learning assume that the backward weights are simply random, as in the feedback alignment algorithm. However, such random weights do not appear to work well for large networks. Here we show how the discontinuity introduced in a spiking system can lead to a solution to this problem. The resulting algorithm is a special case of an estimator used for causal inference in econometrics, regression discontinuity design. We show empirically that this algorithm rapidly makes the backward weights approximate the forward weights. As the backward weights become correct, this improves learning performance over feedback alignment on tasks such as Fashion-MNIST and CIFAR-10. Our results demonstrate that a simple learning rule in a spiking network can allow neurons to produce the right backward connections and thus solve the weight transport problem.
Assessing the Scalability of Biologically-Motivated Deep Learning Algorithms and Architectures
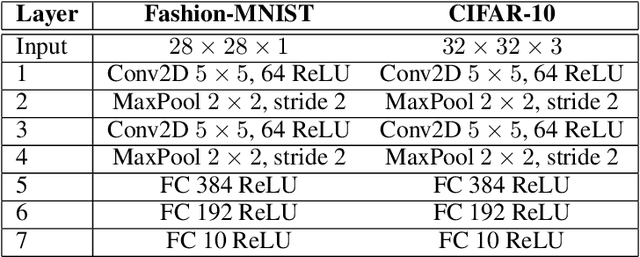
Jul 12, 2018
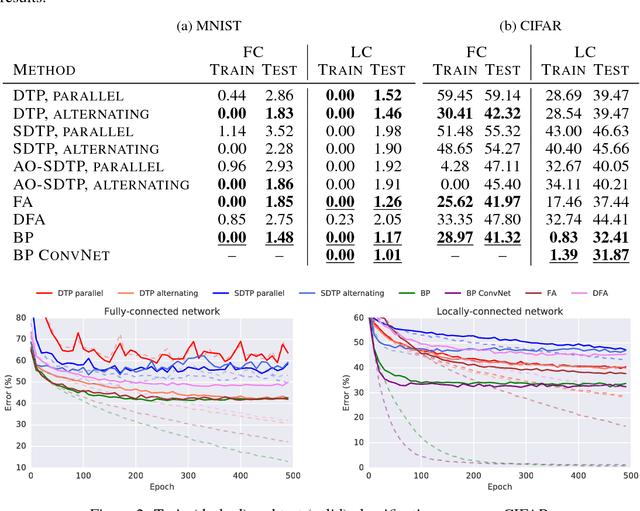
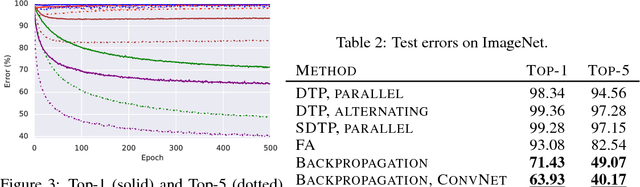

Abstract:The backpropagation of error algorithm (BP) is often said to be impossible to implement in a real brain. The recent success of deep networks in machine learning and AI, however, has inspired proposals for understanding how the brain might learn across multiple layers, and hence how it might implement or approximate BP. As of yet, none of these proposals have been rigorously evaluated on tasks where BP-guided deep learning has proved critical, or in architectures more structured than simple fully-connected networks. Here we present the first results on scaling up biologically motivated models of deep learning on datasets which need deep networks with appropriate architectures to achieve good performance. We present results on the MNIST, CIFAR-10, and ImageNet datasets and explore variants of target-propagation (TP) and feedback alignment (FA) algorithms, and explore performance in both fully- and locally-connected architectures. We also introduce weight-transport-free variants of difference target propagation (DTP) modified to remove backpropagation from the penultimate layer. Many of these algorithms perform well for MNIST, but for CIFAR and ImageNet we find that TP and FA variants perform significantly worse than BP, especially for networks composed of locally connected units, opening questions about whether new architectures and algorithms are required to scale these approaches. Our results and implementation details help establish baselines for biologically motivated deep learning schemes going forward.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge