NOBLE -- Neural Operator with Biologically-informed Latent Embeddings to Capture Experimental Variability in Biological Neuron Models

Characterizing the diverse computational properties of human neurons via multimodal electrophysiological, transcriptomic, and morphological data provides the foundation for constructing and validating bio-realistic neuron models that can advance our understanding of fundamental mechanisms underlying brain function. However, current modeling approaches remain constrained by the limited availability and intrinsic variability of experimental neuronal data. To capture variability, ensembles of deterministic models are often used, but are difficult to scale as model generation requires repeating computationally expensive optimization for each neuron. While deep learning is becoming increasingly relevant in this space, it fails to capture the full biophysical complexity of neurons, their nonlinear voltage dynamics, and variability. To address these shortcomings, we introduce NOBLE, a neural operator framework that learns a mapping from a continuous frequency-modulated embedding of interpretable neuron features to the somatic voltage response induced by current injection. Trained on data generated from biophysically realistic neuron models, NOBLE predicts distributions of neural dynamics accounting for the intrinsic experimental variability. Unlike conventional bio-realistic neuron models, interpolating within the embedding space offers models whose dynamics are consistent with experimentally observed responses. NOBLE is the first scaled-up deep learning framework validated on real experimental data, enabling efficient generation of synthetic neurons that exhibit trial-to-trial variability and achieve a $4200\times$ speedup over numerical solvers. To this end, NOBLE captures fundamental neural properties, opening the door to a better understanding of cellular composition and computations, neuromorphic architectures, large-scale brain circuits, and general neuroAI applications.

Evaluating Sparse Autoencoders: From Shallow Design to Matching Pursuit

Sparse autoencoders (SAEs) have recently become central tools for interpretability, leveraging dictionary learning principles to extract sparse, interpretable features from neural representations whose underlying structure is typically unknown. This paper evaluates SAEs in a controlled setting using MNIST, which reveals that current shallow architectures implicitly rely on a quasi-orthogonality assumption that limits the ability to extract correlated features. To move beyond this, we introduce a multi-iteration SAE by unrolling Matching Pursuit (MP-SAE), enabling the residual-guided extraction of correlated features that arise in hierarchical settings such as handwritten digit generation while guaranteeing monotonic improvement of the reconstruction as more atoms are selected.

EquiReg: Equivariance Regularized Diffusion for Inverse Problems

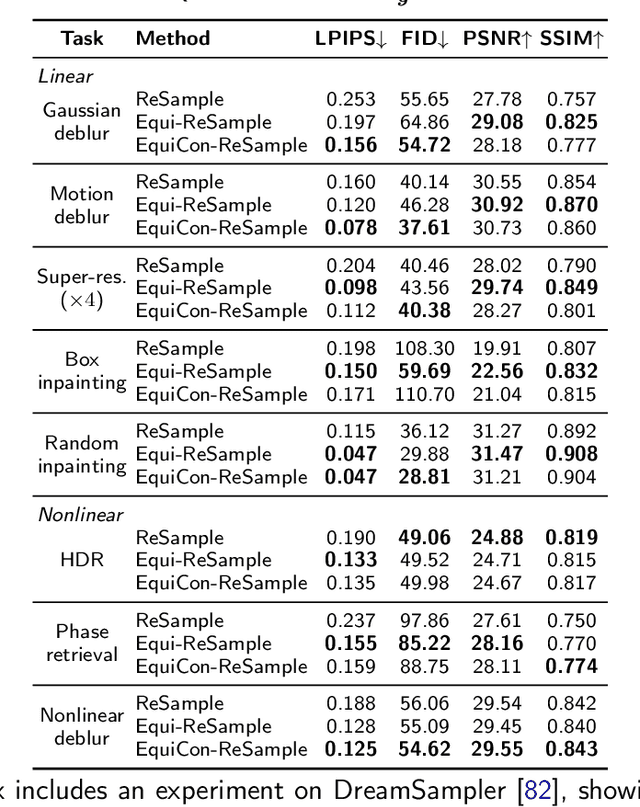
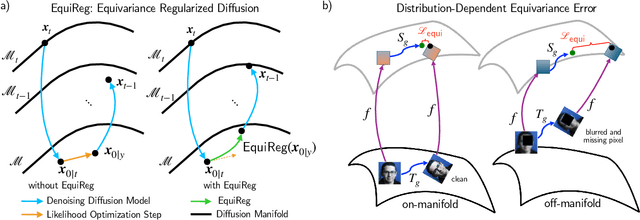
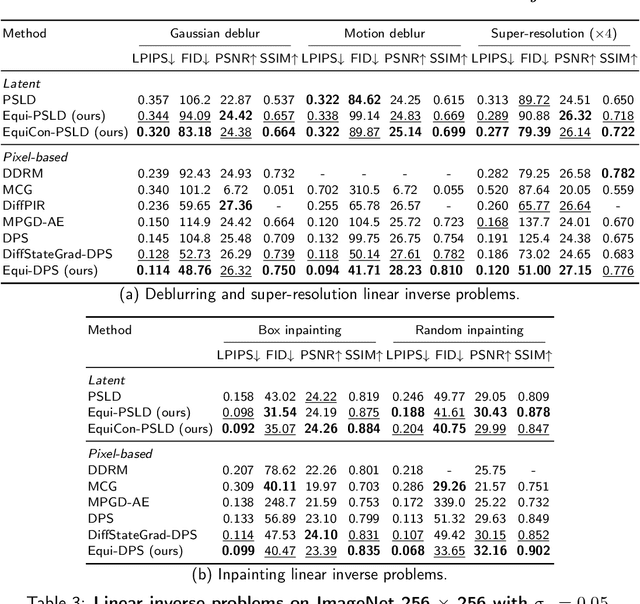
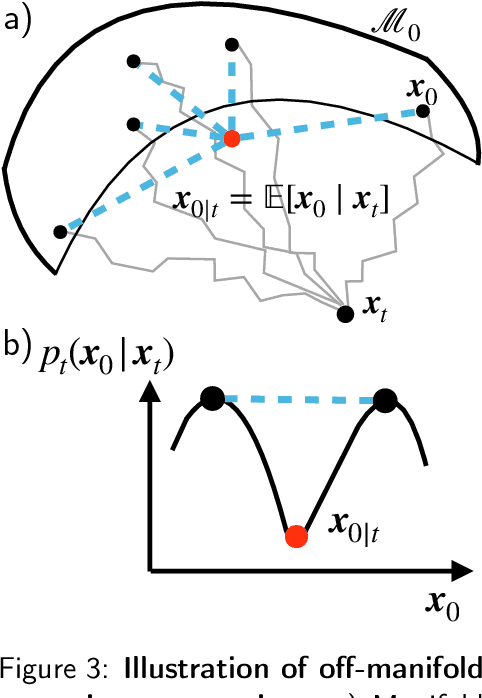
Diffusion models represent the state-of-the-art for solving inverse problems such as image restoration tasks. In the Bayesian framework, diffusion-based inverse solvers incorporate a likelihood term to guide the prior sampling process, generating data consistent with the posterior distribution. However, due to the intractability of the likelihood term, many current methods rely on isotropic Gaussian approximations, which lead to deviations from the data manifold and result in inconsistent, unstable reconstructions. We propose Equivariance Regularized (EquiReg) diffusion, a general framework for regularizing posterior sampling in diffusion-based inverse problem solvers. EquiReg enhances reconstructions by reweighting diffusion trajectories and penalizing those that deviate from the data manifold. We define a new distribution-dependent equivariance error, empirically identify functions that exhibit low error for on-manifold samples and higher error for off-manifold samples, and leverage these functions to regularize the diffusion sampling process. When applied to a variety of solvers, EquiReg outperforms state-of-the-art diffusion models in both linear and nonlinear image restoration tasks, as well as in reconstructing partial differential equations.

Ultrasound Lung Aeration Map via Physics-Aware Neural Operators

Lung ultrasound is a growing modality in clinics for diagnosing and monitoring acute and chronic lung diseases due to its low cost and accessibility. Lung ultrasound works by emitting diagnostic pulses, receiving pressure waves and converting them into radio frequency (RF) data, which are then processed into B-mode images with beamformers for radiologists to interpret. However, unlike conventional ultrasound for soft tissue anatomical imaging, lung ultrasound interpretation is complicated by complex reverberations from the pleural interface caused by the inability of ultrasound to penetrate air. The indirect B-mode images make interpretation highly dependent on reader expertise, requiring years of training, which limits its widespread use despite its potential for high accuracy in skilled hands. To address these challenges and democratize ultrasound lung imaging as a reliable diagnostic tool, we propose LUNA, an AI model that directly reconstructs lung aeration maps from RF data, bypassing the need for traditional beamformers and indirect interpretation of B-mode images. LUNA uses a Fourier neural operator, which processes RF data efficiently in Fourier space, enabling accurate reconstruction of lung aeration maps. LUNA offers a quantitative, reader-independent alternative to traditional semi-quantitative lung ultrasound scoring methods. The development of LUNA involves synthetic and real data: We simulate synthetic data with an experimentally validated approach and scan ex vivo swine lungs as real data. Trained on abundant simulated data and fine-tuned with a small amount of real-world data, LUNA achieves robust performance, demonstrated by an aeration estimation error of 9% in ex-vivo lung scans. We demonstrate the potential of reconstructing lung aeration maps from RF data, providing a foundation for improving lung ultrasound reproducibility and diagnostic utility.

Diffusion State-Guided Projected Gradient for Inverse Problems

Recent advancements in diffusion models have been effective in learning data priors for solving inverse problems. They leverage diffusion sampling steps for inducing a data prior while using a measurement guidance gradient at each step to impose data consistency. For general inverse problems, approximations are needed when an unconditionally trained diffusion model is used since the measurement likelihood is intractable, leading to inaccurate posterior sampling. In other words, due to their approximations, these methods fail to preserve the generation process on the data manifold defined by the diffusion prior, leading to artifacts in applications such as image restoration. To enhance the performance and robustness of diffusion models in solving inverse problems, we propose Diffusion State-Guided Projected Gradient (DiffStateGrad), which projects the measurement gradient onto a subspace that is a low-rank approximation of an intermediate state of the diffusion process. DiffStateGrad, as a module, can be added to a wide range of diffusion-based inverse solvers to improve the preservation of the diffusion process on the prior manifold and filter out artifact-inducing components. We highlight that DiffStateGrad improves the robustness of diffusion models in terms of the choice of measurement guidance step size and noise while improving the worst-case performance. Finally, we demonstrate that DiffStateGrad improves upon the state-of-the-art on linear and nonlinear image restoration inverse problems.

Fourier Neural Operators for Learning Dynamics in Quantum Spin Systems

Fourier Neural Operators (FNOs) excel on tasks using functional data, such as those originating from partial differential equations. Such characteristics render them an effective approach for simulating the time evolution of quantum wavefunctions, which is a computationally challenging, yet coveted task for understanding quantum systems. In this manuscript, we use FNOs to model the evolution of random quantum spin systems, so chosen due to their representative quantum dynamics and minimal symmetry. We explore two distinct FNO architectures and examine their performance for learning and predicting time evolution using both random and low-energy input states. Additionally, we apply FNOs to a compact set of Hamiltonian observables ($\sim\text{poly}(n)$) instead of the entire $2^n$ quantum wavefunction, which greatly reduces the size of our inputs and outputs and, consequently, the requisite dimensions of the resulting FNOs. Moreover, this Hamiltonian observable-based method demonstrates that FNOs can effectively distill information from high-dimensional spaces into lower-dimensional spaces. The extrapolation of Hamiltonian observables to times later than those used in training is of particular interest, as this stands to fundamentally increase the simulatability of quantum systems past both the coherence times of contemporary quantum architectures and the circuit-depths of tractable tensor networks.

Probabilistic Unrolling: Scalable, Inverse-Free Maximum Likelihood Estimation for Latent Gaussian Models

Latent Gaussian models have a rich history in statistics and machine learning, with applications ranging from factor analysis to compressed sensing to time series analysis. The classical method for maximizing the likelihood of these models is the expectation-maximization (EM) algorithm. For problems with high-dimensional latent variables and large datasets, EM scales poorly because it needs to invert as many large covariance matrices as the number of data points. We introduce probabilistic unrolling, a method that combines Monte Carlo sampling with iterative linear solvers to circumvent matrix inversion. Our theoretical analyses reveal that unrolling and backpropagation through the iterations of the solver can accelerate gradient estimation for maximum likelihood estimation. In experiments on simulated and real data, we demonstrate that probabilistic unrolling learns latent Gaussian models up to an order of magnitude faster than gradient EM, with minimal losses in model performance.

Learning Filter-Based Compressed Blind-Deconvolution

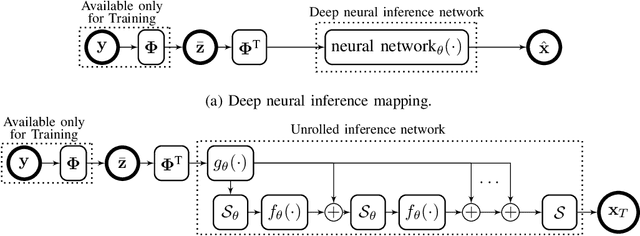
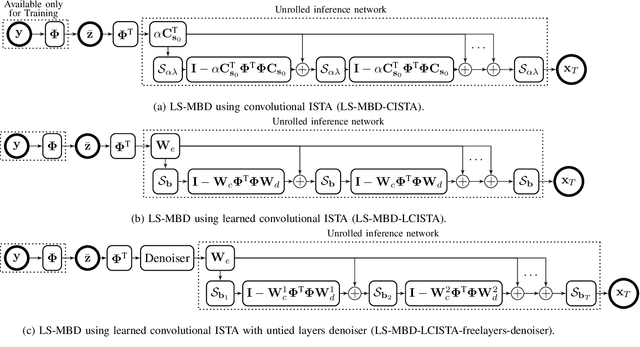
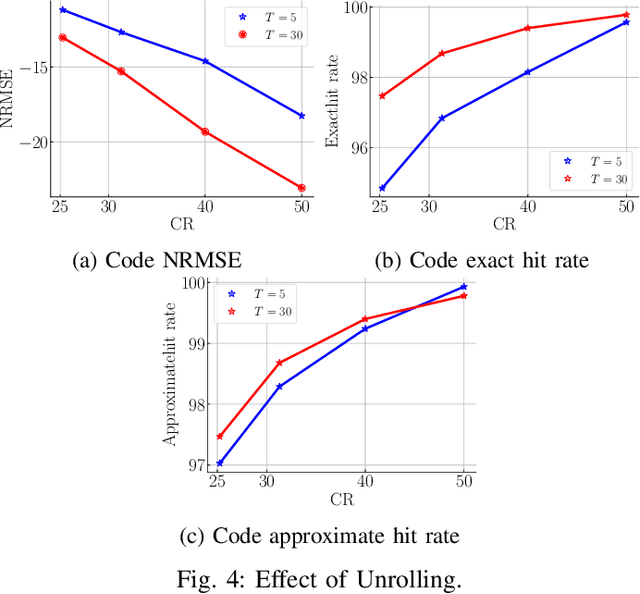
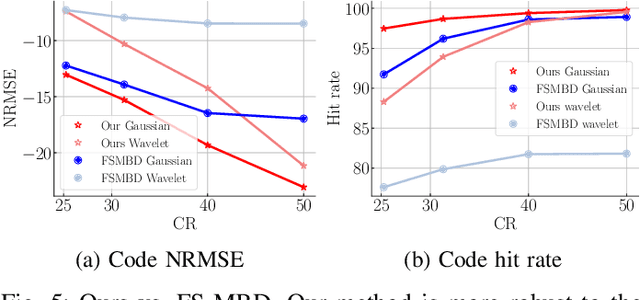
The problem of sparse multichannel blind deconvolution (S-MBD) arises frequently in many engineering applications such as radar/sonar/ultrasound imaging. To reduce its computational and implementation cost, we propose a compression method that enables blind recovery from much fewer measurements with respect to the full received signal in time. The proposed compression measures the signal through a filter followed by a subsampling, allowing for a significant reduction in implementation cost. We derive theoretical guarantees for the identifiability and recovery of a sparse filter from compressed measurements. Our results allow for the design of a wide class of compression filters. We, then, propose a data-driven unrolled learning framework to learn the compression filter and solve the S-MBD problem. The encoder is a recurrent inference network that maps compressed measurements into an estimate of sparse filters. We demonstrate that our unrolled learning method is more robust to choices of source shapes and has better recovery performance compared to optimization-based methods. Finally, in applications with limited data (fewshot learning), we highlight the superior generalization capability of unrolled learning compared to conventional deep learning.

A Training Framework for Stereo-Aware Speech Enhancement using Deep Neural Networks

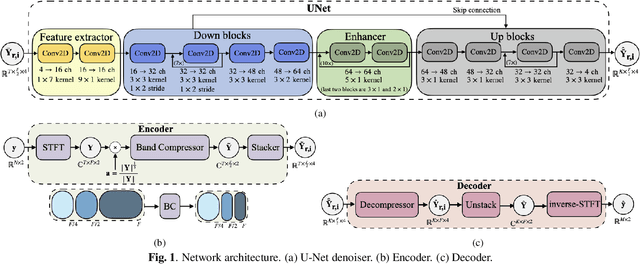
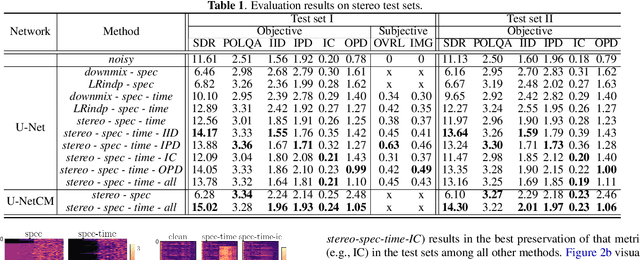
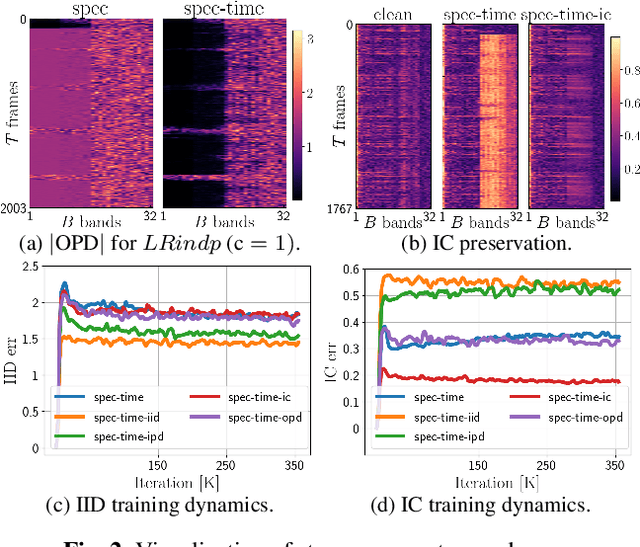
Deep learning-based speech enhancement has shown unprecedented performance in recent years. The most popular mono speech enhancement frameworks are end-to-end networks mapping the noisy mixture into an estimate of the clean speech. With growing computational power and availability of multichannel microphone recordings, prior works have aimed to incorporate spatial statistics along with spectral information to boost up performance. Despite an improvement in enhancement performance of mono output, the spatial image preservation and subjective evaluations have not gained much attention in the literature. This paper proposes a novel stereo-aware framework for speech enhancement, i.e., a training loss for deep learning-based speech enhancement to preserve the spatial image while enhancing the stereo mixture. The proposed framework is model independent, hence it can be applied to any deep learning based architecture. We provide an extensive objective and subjective evaluation of the trained models through a listening test. We show that by regularizing for an image preservation loss, the overall performance is improved, and the stereo aspect of the speech is better preserved.

PUDLE: Implicit Acceleration of Dictionary Learning by Backpropagation

The dictionary learning problem, representing data as a combination of few atoms, has long stood as a popular method for learning representations in statistics and signal processing. The most popular dictionary learning algorithm alternates between sparse coding and dictionary update steps, and a rich literature has studied its theoretical convergence. The growing popularity of neurally plausible unfolded sparse coding networks has led to the empirical finding that backpropagation through such networks performs dictionary learning. This paper offers the first theoretical proof for these empirical results through PUDLE, a Provable Unfolded Dictionary LEarning method. We highlight the impact of loss, unfolding, and backpropagation on convergence. We discover an implicit acceleration: as a function of unfolding, the backpropagated gradient converges faster and is more accurate than the gradient from alternating minimization. We complement our findings through synthetic and image denoising experiments. The findings support the use of accelerated deep learning optimizers and unfolded networks for dictionary learning.