EquiReg: Equivariance Regularized Diffusion for Inverse Problems

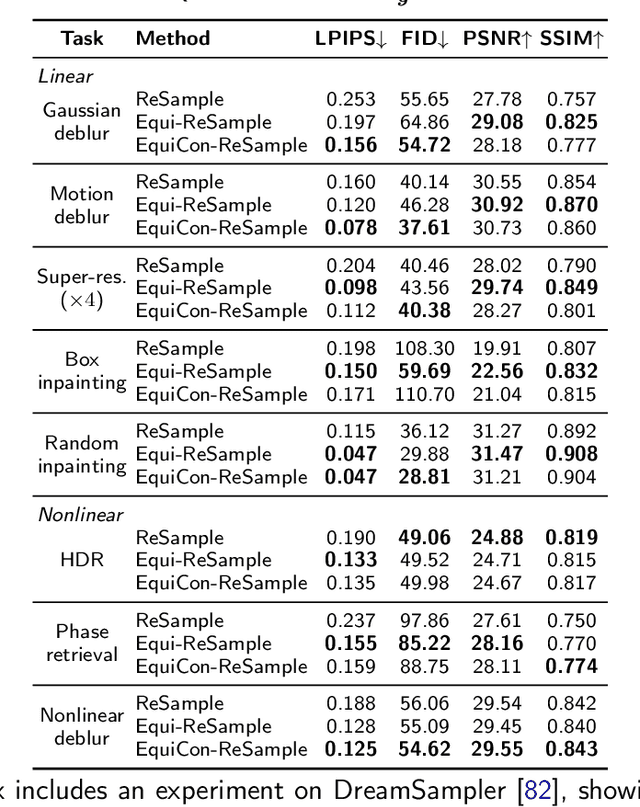
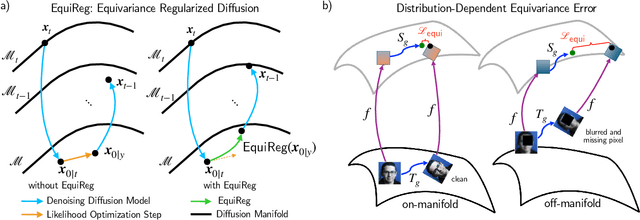
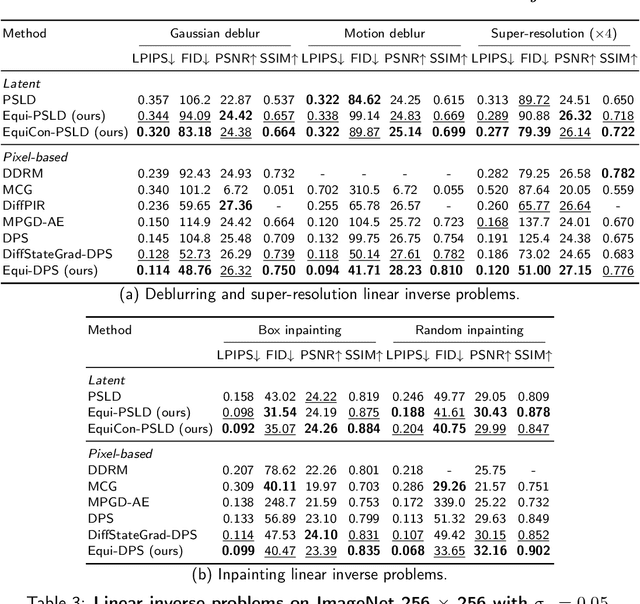
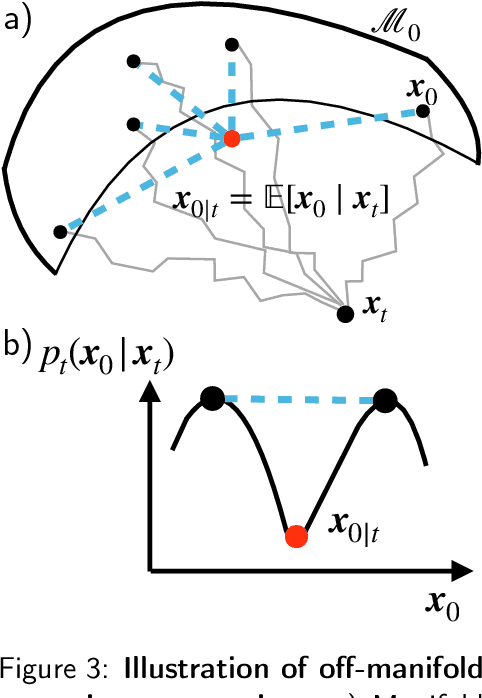
Diffusion models represent the state-of-the-art for solving inverse problems such as image restoration tasks. In the Bayesian framework, diffusion-based inverse solvers incorporate a likelihood term to guide the prior sampling process, generating data consistent with the posterior distribution. However, due to the intractability of the likelihood term, many current methods rely on isotropic Gaussian approximations, which lead to deviations from the data manifold and result in inconsistent, unstable reconstructions. We propose Equivariance Regularized (EquiReg) diffusion, a general framework for regularizing posterior sampling in diffusion-based inverse problem solvers. EquiReg enhances reconstructions by reweighting diffusion trajectories and penalizing those that deviate from the data manifold. We define a new distribution-dependent equivariance error, empirically identify functions that exhibit low error for on-manifold samples and higher error for off-manifold samples, and leverage these functions to regularize the diffusion sampling process. When applied to a variety of solvers, EquiReg outperforms state-of-the-art diffusion models in both linear and nonlinear image restoration tasks, as well as in reconstructing partial differential equations.

Diffusion State-Guided Projected Gradient for Inverse Problems

Recent advancements in diffusion models have been effective in learning data priors for solving inverse problems. They leverage diffusion sampling steps for inducing a data prior while using a measurement guidance gradient at each step to impose data consistency. For general inverse problems, approximations are needed when an unconditionally trained diffusion model is used since the measurement likelihood is intractable, leading to inaccurate posterior sampling. In other words, due to their approximations, these methods fail to preserve the generation process on the data manifold defined by the diffusion prior, leading to artifacts in applications such as image restoration. To enhance the performance and robustness of diffusion models in solving inverse problems, we propose Diffusion State-Guided Projected Gradient (DiffStateGrad), which projects the measurement gradient onto a subspace that is a low-rank approximation of an intermediate state of the diffusion process. DiffStateGrad, as a module, can be added to a wide range of diffusion-based inverse solvers to improve the preservation of the diffusion process on the prior manifold and filter out artifact-inducing components. We highlight that DiffStateGrad improves the robustness of diffusion models in terms of the choice of measurement guidance step size and noise while improving the worst-case performance. Finally, we demonstrate that DiffStateGrad improves upon the state-of-the-art on linear and nonlinear image restoration inverse problems.