EquiReg: Equivariance Regularized Diffusion for Inverse Problems

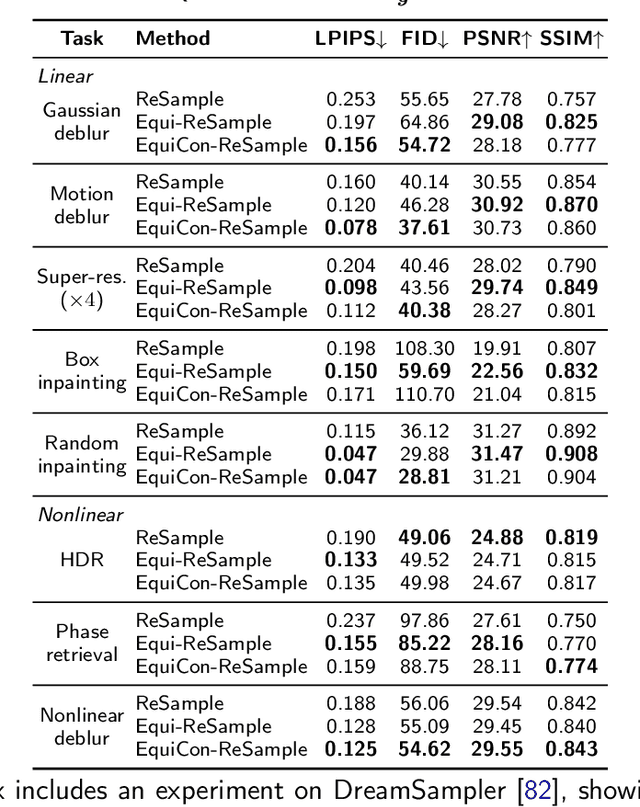
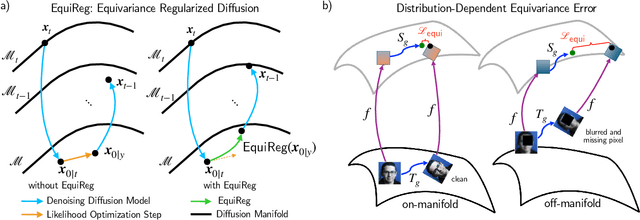
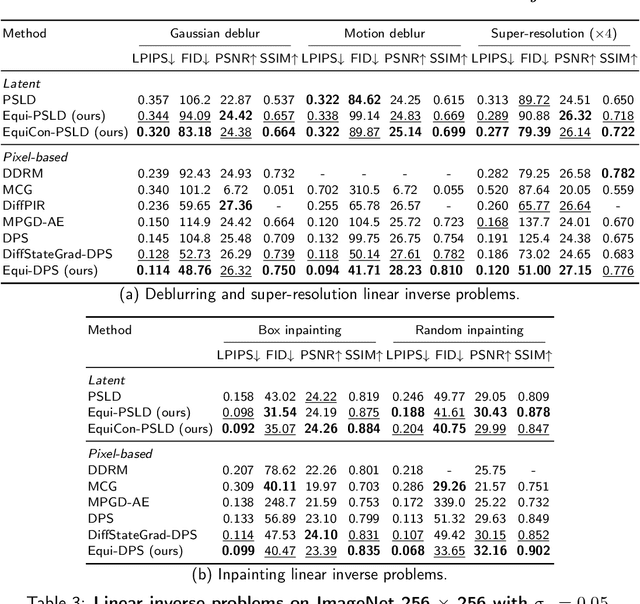
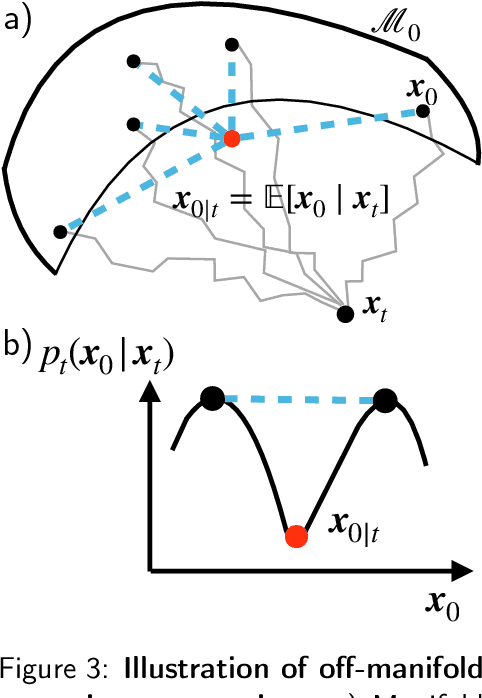
Diffusion models represent the state-of-the-art for solving inverse problems such as image restoration tasks. In the Bayesian framework, diffusion-based inverse solvers incorporate a likelihood term to guide the prior sampling process, generating data consistent with the posterior distribution. However, due to the intractability of the likelihood term, many current methods rely on isotropic Gaussian approximations, which lead to deviations from the data manifold and result in inconsistent, unstable reconstructions. We propose Equivariance Regularized (EquiReg) diffusion, a general framework for regularizing posterior sampling in diffusion-based inverse problem solvers. EquiReg enhances reconstructions by reweighting diffusion trajectories and penalizing those that deviate from the data manifold. We define a new distribution-dependent equivariance error, empirically identify functions that exhibit low error for on-manifold samples and higher error for off-manifold samples, and leverage these functions to regularize the diffusion sampling process. When applied to a variety of solvers, EquiReg outperforms state-of-the-art diffusion models in both linear and nonlinear image restoration tasks, as well as in reconstructing partial differential equations.

Guided Diffusion Sampling on Function Spaces with Applications to PDEs

We propose a general framework for conditional sampling in PDE-based inverse problems, targeting the recovery of whole solutions from extremely sparse or noisy measurements. This is accomplished by a function-space diffusion model and plug-and-play guidance for conditioning. Our method first trains an unconditional discretization-agnostic denoising model using neural operator architectures. At inference, we refine the samples to satisfy sparse observation data via a gradient-based guidance mechanism. Through rigorous mathematical analysis, we extend Tweedie's formula to infinite-dimensional Hilbert spaces, providing the theoretical foundation for our posterior sampling approach. Our method (FunDPS) accurately captures posterior distributions in function spaces under minimal supervision and severe data scarcity. Across five PDE tasks with only 3% observation, our method achieves an average 32% accuracy improvement over state-of-the-art fixed-resolution diffusion baselines while reducing sampling steps by 4x. Furthermore, multi-resolution fine-tuning ensures strong cross-resolution generalizability. To the best of our knowledge, this is the first diffusion-based framework to operate independently of discretization, offering a practical and flexible solution for forward and inverse problems in the context of PDEs. Code is available at https://github.com/neuraloperator/FunDPS

Amortized Posterior Sampling with Diffusion Prior Distillation

We propose a variational inference approach to sample from the posterior distribution for solving inverse problems. From a pre-trained diffusion model, our approach trains a conditional flow model to minimize the divergence between the proposal variational distribution and the posterior distribution implicitly defined through the diffusion model. Once trained, the flow model is capable of sampling from the posterior distribution with a single NFE, amortized with respect to the measurement. The proposed method paves a new path for distilling a diffusion prior for efficient posterior sampling. We show that our method is applicable to standard signals in Euclidean space, as well as signals on manifold.

Defining Neural Network Architecture through Polytope Structures of Dataset

Current theoretical and empirical research in neural networks suggests that complex datasets require large network architectures for thorough classification, yet the precise nature of this relationship remains unclear. This paper tackles this issue by defining upper and lower bounds for neural network widths, which are informed by the polytope structure of the dataset in question. We also delve into the application of these principles to simplicial complexes and specific manifold shapes, explaining how the requirement for network width varies in accordance with the geometric complexity of the dataset. Moreover, we develop an algorithm to investigate a converse situation where the polytope structure of a dataset can be inferred from its corresponding trained neural networks. Through our algorithm, it is established that popular datasets such as MNIST, Fashion-MNIST, and CIFAR10 can be efficiently encapsulated using no more than two polytopes with a small number of faces.