Probabilistic Unrolling: Scalable, Inverse-Free Maximum Likelihood Estimation for Latent Gaussian Models

Latent Gaussian models have a rich history in statistics and machine learning, with applications ranging from factor analysis to compressed sensing to time series analysis. The classical method for maximizing the likelihood of these models is the expectation-maximization (EM) algorithm. For problems with high-dimensional latent variables and large datasets, EM scales poorly because it needs to invert as many large covariance matrices as the number of data points. We introduce probabilistic unrolling, a method that combines Monte Carlo sampling with iterative linear solvers to circumvent matrix inversion. Our theoretical analyses reveal that unrolling and backpropagation through the iterations of the solver can accelerate gradient estimation for maximum likelihood estimation. In experiments on simulated and real data, we demonstrate that probabilistic unrolling learns latent Gaussian models up to an order of magnitude faster than gradient EM, with minimal losses in model performance.

A fast asynchronous MCMC sampler for sparse Bayesian inference

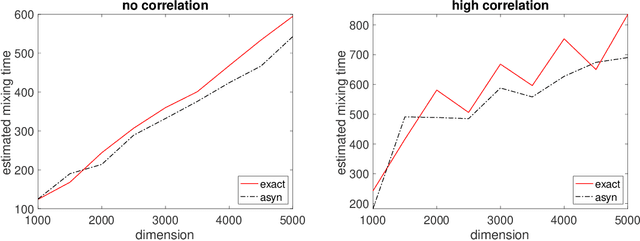
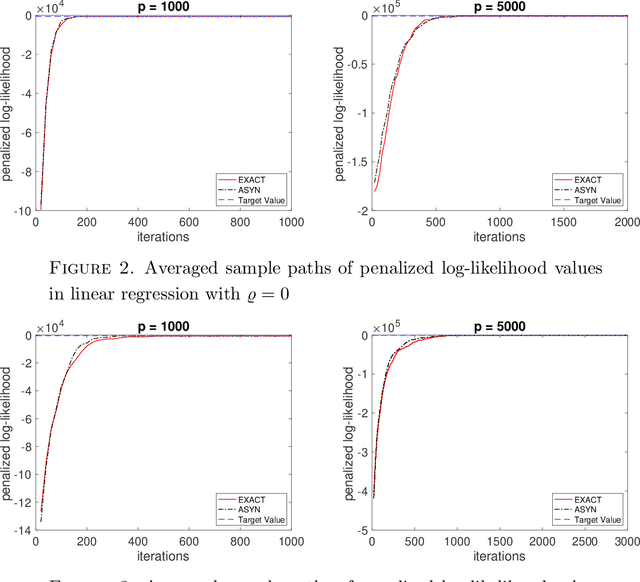
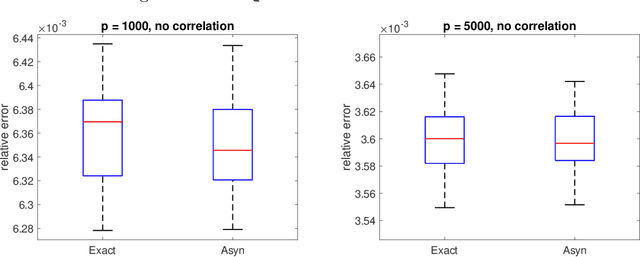
We propose a very fast approximate Markov Chain Monte Carlo (MCMC) sampling framework that is applicable to a large class of sparse Bayesian inference problems, where the computational cost per iteration in several models is of order $O(ns)$, where $n$ is the sample size, and $s$ the underlying sparsity of the model. This cost can be further reduced by data sub-sampling when stochastic gradient Langevin dynamics are employed. The algorithm is an extension of the asynchronous Gibbs sampler of Johnson et al. (2013), but can be viewed from a statistical perspective as a form of Bayesian iterated sure independent screening (Fan et al. (2009)). We show that in high-dimensional linear regression problems, the Markov chain generated by the proposed algorithm admits an invariant distribution that recovers correctly the main signal with high probability under some statistical assumptions. Furthermore we show that its mixing time is at most linear in the number of regressors. We illustrate the algorithm with several models.

On Russian Roulette Estimates for Bayesian Inference with Doubly-Intractable Likelihoods

A large number of statistical models are "doubly-intractable": the likelihood normalising term, which is a function of the model parameters, is intractable, as well as the marginal likelihood (model evidence). This means that standard inference techniques to sample from the posterior, such as Markov chain Monte Carlo (MCMC), cannot be used. Examples include, but are not confined to, massive Gaussian Markov random fields, autologistic models and Exponential random graph models. A number of approximate schemes based on MCMC techniques, Approximate Bayesian computation (ABC) or analytic approximations to the posterior have been suggested, and these are reviewed here. Exact MCMC schemes, which can be applied to a subset of doubly-intractable distributions, have also been developed and are described in this paper. As yet, no general method exists which can be applied to all classes of models with doubly-intractable posteriors. In addition, taking inspiration from the Physics literature, we study an alternative method based on representing the intractable likelihood as an infinite series. Unbiased estimates of the likelihood can then be obtained by finite time stochastic truncation of the series via Russian Roulette sampling, although the estimates are not necessarily positive. Results from the Quantum Chromodynamics literature are exploited to allow the use of possibly negative estimates in a pseudo-marginal MCMC scheme such that expectations with respect to the posterior distribution are preserved. The methodology is reviewed on well-known examples such as the parameters in Ising models, the posterior for Fisher-Bingham distributions on the $d$-Sphere and a large-scale Gaussian Markov Random Field model describing the Ozone Column data. This leads to a critical assessment of the strengths and weaknesses of the methodology with pointers to ongoing research.