Ranking in Contextual Multi-Armed Bandits

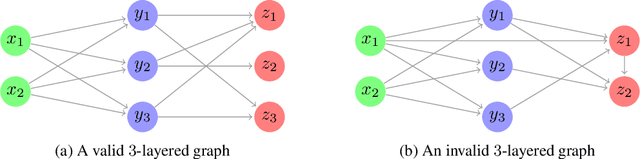
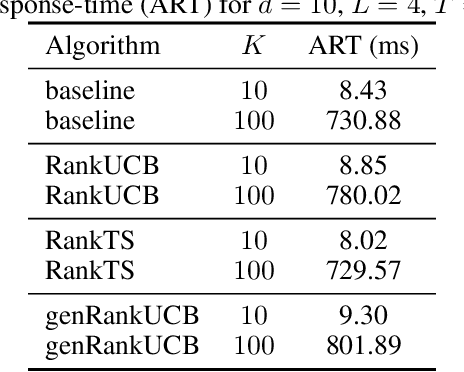
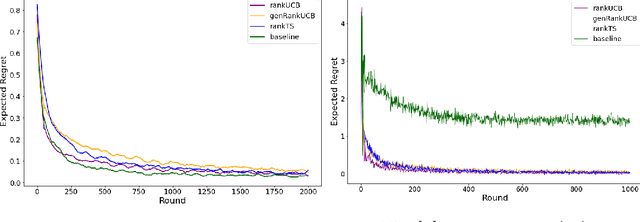
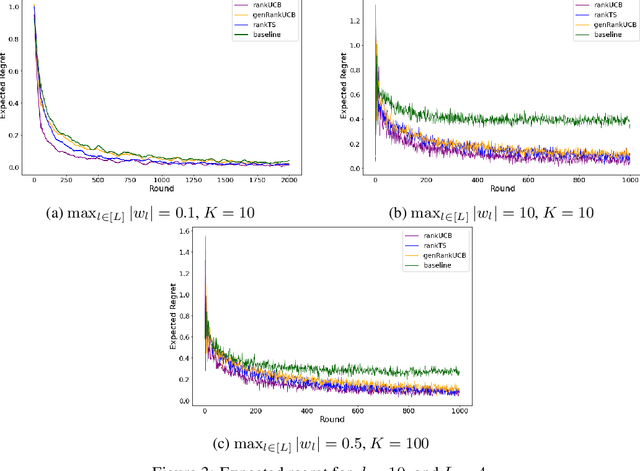
We study a ranking problem in the contextual multi-armed bandit setting. A learning agent selects an ordered list of items at each time step and observes stochastic outcomes for each position. In online recommendation systems, showing an ordered list of the most attractive items would not be the best choice since both position and item dependencies result in a complicated reward function. A very naive example is the lack of diversity when all the most attractive items are from the same category. We model position and item dependencies in the ordered list and design UCB and Thompson Sampling type algorithms for this problem. We prove that the regret bound over $T$ rounds and $L$ positions is $\Tilde{O}(L\sqrt{d T})$, which has the same order as the previous works with respect to $T$ and only increases linearly with $L$. Our work generalizes existing studies in several directions, including position dependencies where position discount is a particular case, and proposes a more general contextual bandit model.

Conformal Off-Policy Prediction in Contextual Bandits

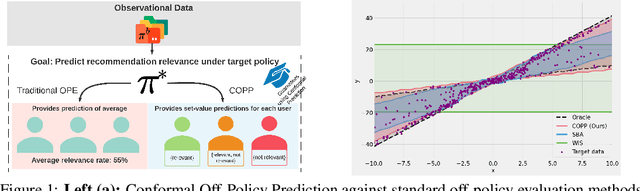
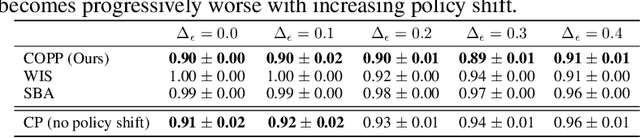
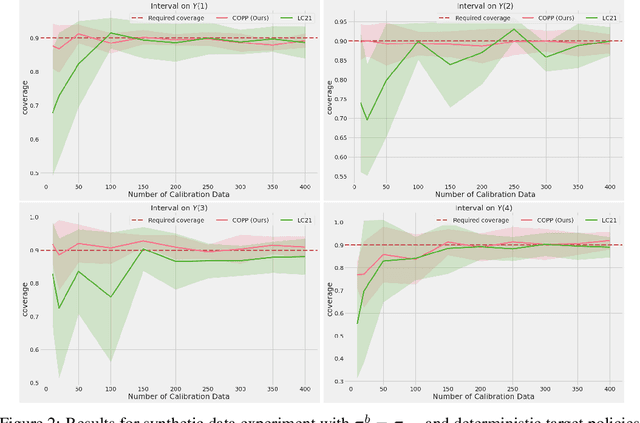
Most off-policy evaluation methods for contextual bandits have focused on the expected outcome of a policy, which is estimated via methods that at best provide only asymptotic guarantees. However, in many applications, the expectation may not be the best measure of performance as it does not capture the variability of the outcome. In addition, particularly in safety-critical settings, stronger guarantees than asymptotic correctness may be required. To address these limitations, we consider a novel application of conformal prediction to contextual bandits. Given data collected under a behavioral policy, we propose \emph{conformal off-policy prediction} (COPP), which can output reliable predictive intervals for the outcome under a new target policy. We provide theoretical finite-sample guarantees without making any additional assumptions beyond the standard contextual bandit setup, and empirically demonstrate the utility of COPP compared with existing methods on synthetic and real-world data.

A Continuous Time Framework for Discrete Denoising Models

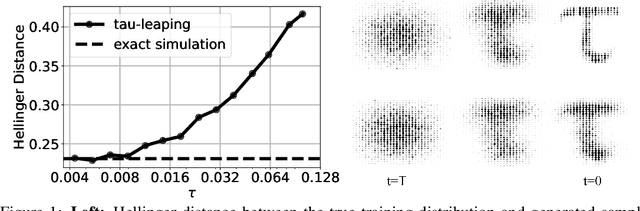
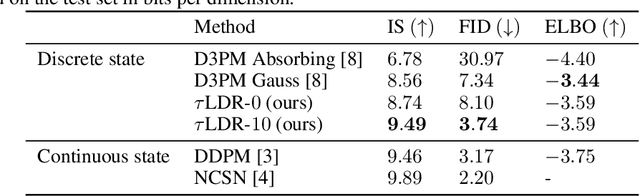
We provide the first complete continuous time framework for denoising diffusion models of discrete data. This is achieved by formulating the forward noising process and corresponding reverse time generative process as Continuous Time Markov Chains (CTMCs). The model can be efficiently trained using a continuous time version of the ELBO. We simulate the high dimensional CTMC using techniques developed in chemical physics and exploit our continuous time framework to derive high performance samplers that we show can outperform discrete time methods for discrete data. The continuous time treatment also enables us to derive a novel theoretical result bounding the error between the generated sample distribution and the true data distribution.

Towards Learning Universal Hyperparameter Optimizers with Transformers

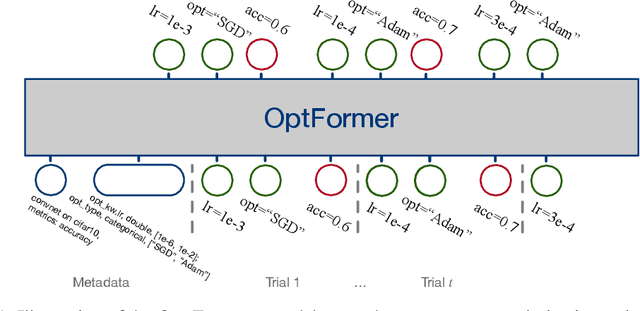
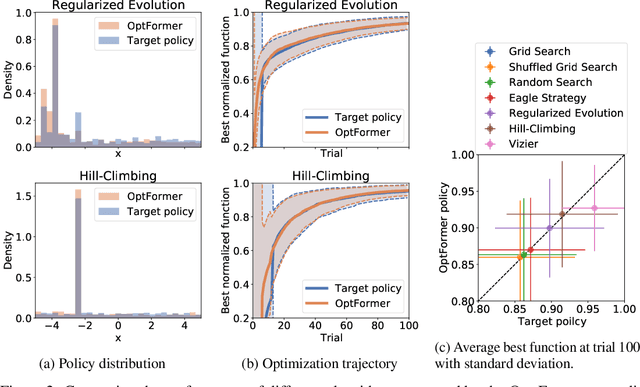
Meta-learning hyperparameter optimization (HPO) algorithms from prior experiments is a promising approach to improve optimization efficiency over objective functions from a similar distribution. However, existing methods are restricted to learning from experiments sharing the same set of hyperparameters. In this paper, we introduce the OptFormer, the first text-based Transformer HPO framework that provides a universal end-to-end interface for jointly learning policy and function prediction when trained on vast tuning data from the wild. Our extensive experiments demonstrate that the OptFormer can imitate at least 7 different HPO algorithms, which can be further improved via its function uncertainty estimates. Compared to a Gaussian Process, the OptFormer also learns a robust prior distribution for hyperparameter response functions, and can thereby provide more accurate and better calibrated predictions. This work paves the path to future extensions for training a Transformer-based model as a general HPO optimizer.

Chained Generalisation Bounds

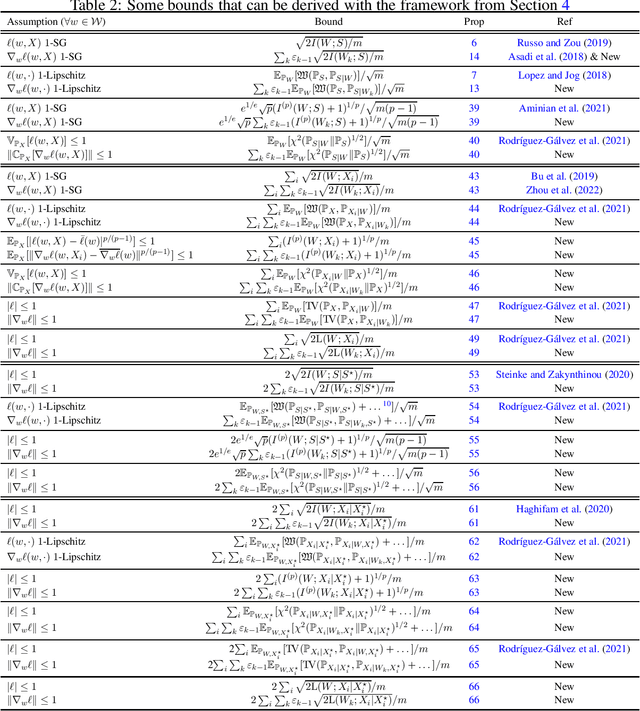
This work discusses how to derive upper bounds for the expected generalisation error of supervised learning algorithms by means of the chaining technique. By developing a general theoretical framework, we establish a duality between generalisation bounds based on the regularity of the loss function, and their chained counterparts, which can be obtained by lifting the regularity assumption from the loss onto its gradient. This allows us to re-derive the chaining mutual information bound from the literature, and to obtain novel chained information-theoretic generalisation bounds, based on the Wasserstein distance and other probability metrics. We show on some toy examples that the chained generalisation bound can be significantly tighter than its standard counterpart, particularly when the distribution of the hypotheses selected by the algorithm is very concentrated. Keywords: Generalisation bounds; Chaining; Information-theoretic bounds; Mutual information; Wasserstein distance; PAC-Bayes.

Conditional Simulation Using Diffusion Schrödinger Bridges

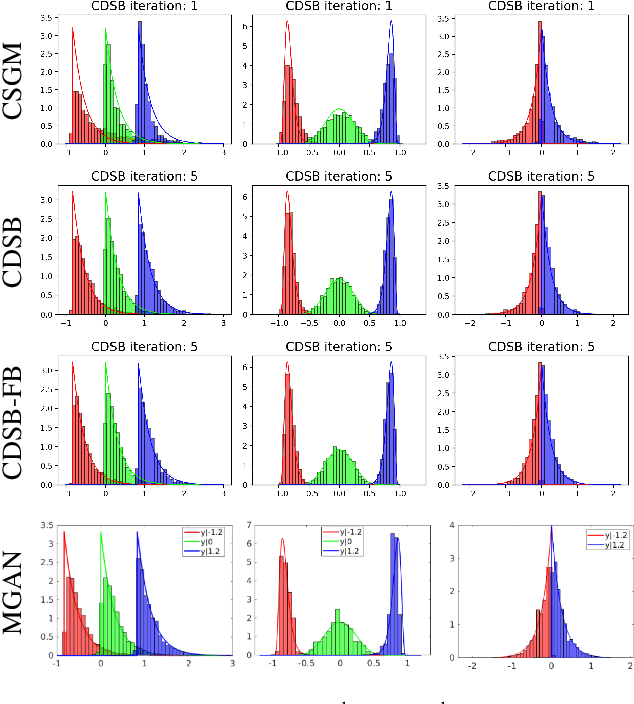
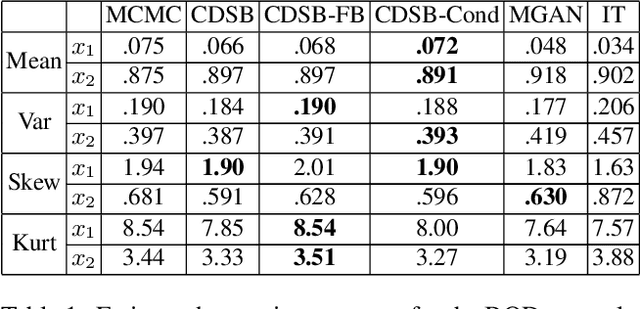
Denoising diffusion models have recently emerged as a powerful class of generative models. They provide state-of-the-art results, not only for unconditional simulation, but also when used to solve conditional simulation problems arising in a wide range of inverse problems such as image inpainting or deblurring. A limitation of these models is that they are computationally intensive at generation time as they require simulating a diffusion process over a long time horizon. When performing unconditional simulation, a Schr\"odinger bridge formulation of generative modeling leads to a theoretically grounded algorithm shortening generation time which is complementary to other proposed acceleration techniques. We extend here the Schr\"odinger bridge framework to conditional simulation. We demonstrate this novel methodology on various applications including image super-resolution and optimal filtering for state-space models.

On PAC-Bayesian reconstruction guarantees for VAEs

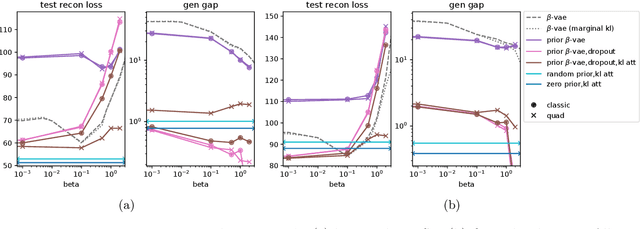
Despite its wide use and empirical successes, the theoretical understanding and study of the behaviour and performance of the variational autoencoder (VAE) have only emerged in the past few years. We contribute to this recent line of work by analysing the VAE's reconstruction ability for unseen test data, leveraging arguments from the PAC-Bayes theory. We provide generalisation bounds on the theoretical reconstruction error, and provide insights on the regularisation effect of VAE objectives. We illustrate our theoretical results with supporting experiments on classical benchmark datasets.

Riemannian Score-Based Generative Modeling

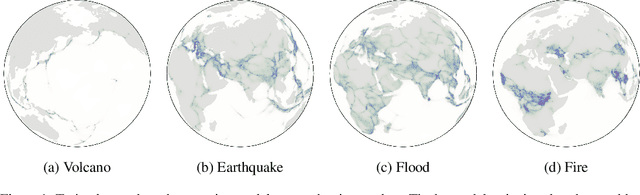
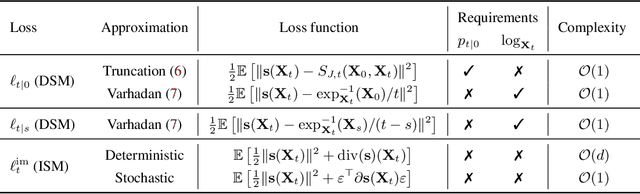
Score-based generative models (SGMs) are a novel class of generative models demonstrating remarkable empirical performance. One uses a diffusion to add progressively Gaussian noise to the data, while the generative model is a "denoising" process obtained by approximating the time-reversal of this "noising" diffusion. However, current SGMs make the underlying assumption that the data is supported on a Euclidean manifold with flat geometry. This prevents the use of these models for applications in robotics, geoscience or protein modeling which rely on distributions defined on Riemannian manifolds. To overcome this issue, we introduce Riemannian Score-based Generative Models (RSGMs) which extend current SGMs to the setting of compact Riemannian manifolds. We illustrate our approach with earth and climate science data and show how RSGMs can be accelerated by solving a Schr\"odinger bridge problem on manifolds.

Importance Weighting Approach in Kernel Bayes' Rule

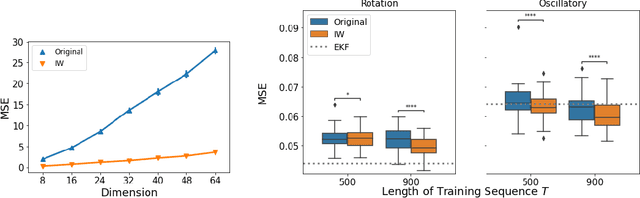
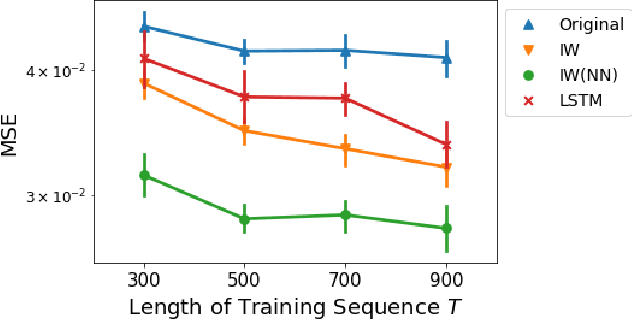
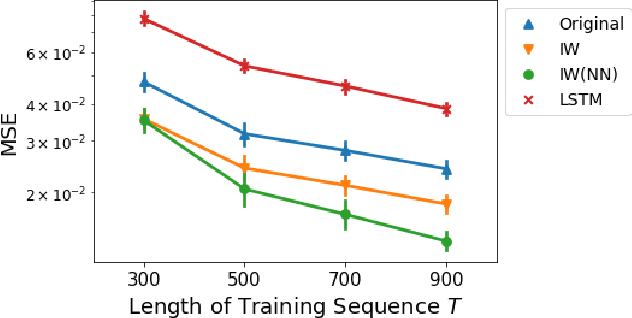
We study a nonparametric approach to Bayesian computation via feature means, where the expectation of prior features is updated to yield expected posterior features, based on regression from kernel or neural net features of the observations. All quantities involved in the Bayesian update are learned from observed data, making the method entirely model-free. The resulting algorithm is a novel instance of a kernel Bayes' rule (KBR). Our approach is based on importance weighting, which results in superior numerical stability to the existing approach to KBR, which requires operator inversion. We show the convergence of the estimator using a novel consistency analysis on the importance weighting estimator in the infinity norm. We evaluate our KBR on challenging synthetic benchmarks, including a filtering problem with a state-space model involving high dimensional image observations. The proposed method yields uniformly better empirical performance than the existing KBR, and competitive performance with other competing methods.

Continual Repeated Annealed Flow Transport Monte Carlo

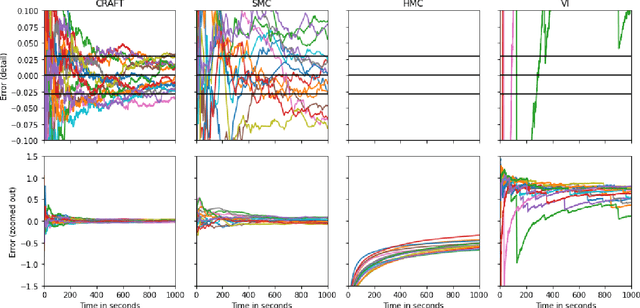
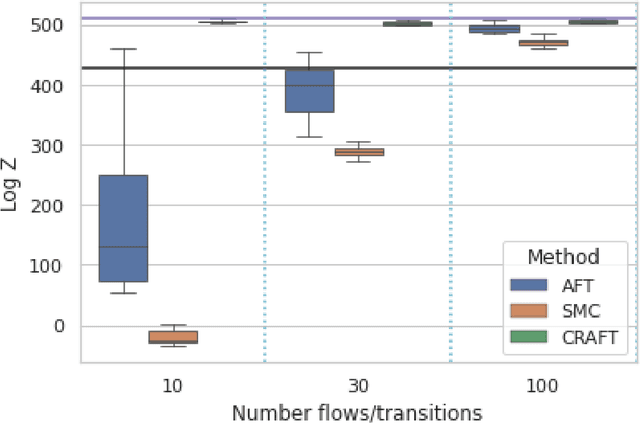
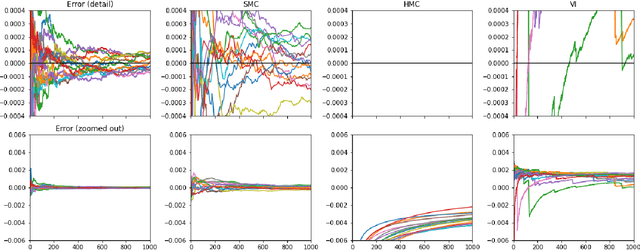
We propose Continual Repeated Annealed Flow Transport Monte Carlo (CRAFT), a method that combines a sequential Monte Carlo (SMC) sampler (itself a generalization of Annealed Importance Sampling) with variational inference using normalizing flows. The normalizing flows are directly trained to transport between annealing temperatures using a KL divergence for each transition. This optimization objective is itself estimated using the normalizing flow/SMC approximation. We show conceptually and using multiple empirical examples that CRAFT improves on Annealed Flow Transport Monte Carlo (Arbel et al., 2021), on which it builds and also on Markov chain Monte Carlo (MCMC) based Stochastic Normalizing Flows (Wu et al., 2020). By incorporating CRAFT within particle MCMC, we show that such learnt samplers can achieve impressively accurate results on a challenging lattice field theory example.