Single-Pass Pivot Algorithm for Correlation Clustering. Keep it simple!

We show that a simple single-pass semi-streaming variant of the Pivot algorithm for Correlation Clustering gives a (3 + {\epsilon})-approximation using O(n/{\epsilon}) words of memory. This is a slight improvement over the recent results of Cambus, Kuhn, Lindy, Pai, and Uitto, who gave a (3 + {\epsilon})-approximation using O(n log n) words of memory, and Behnezhad, Charikar, Ma, and Tan, who gave a 5-approximation using O(n) words of memory. One of the main contributions of this paper is that both the algorithm and its analysis are very simple, and also the algorithm is easy to implement.

Explainable k-means. Don't be greedy, plant bigger trees!

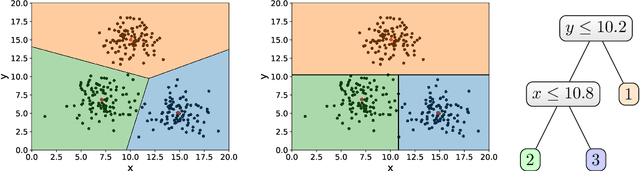
We provide a new bi-criteria $\tilde{O}(\log^2 k)$ competitive algorithm for explainable $k$-means clustering. Explainable $k$-means was recently introduced by Dasgupta, Frost, Moshkovitz, and Rashtchian (ICML 2020). It is described by an easy to interpret and understand (threshold) decision tree or diagram. The cost of the explainable $k$-means clustering equals to the sum of costs of its clusters; and the cost of each cluster equals the sum of squared distances from the points in the cluster to the center of that cluster. Our randomized bi-criteria algorithm constructs a threshold decision tree that partitions the data set into $(1+\delta)k$ clusters (where $\delta\in (0,1)$ is a parameter of the algorithm). The cost of this clustering is at most $\tilde{O}(1/\delta \cdot \log^2 k)$ times the cost of the optimal unconstrained $k$-means clustering. We show that this bound is almost optimal.

Local Correlation Clustering with Asymmetric Classification Errors

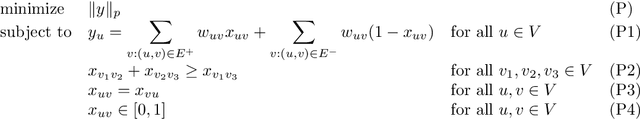
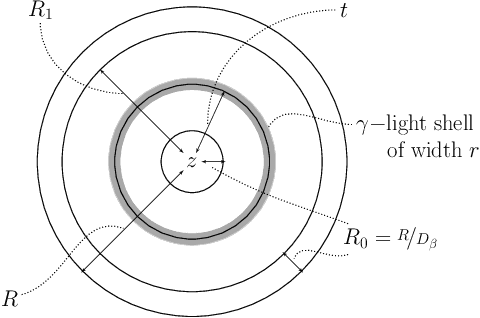
In the Correlation Clustering problem, we are given a complete weighted graph $G$ with its edges labeled as "similar" and "dissimilar" by a noisy binary classifier. For a clustering $\mathcal{C}$ of graph $G$, a similar edge is in disagreement with $\mathcal{C}$, if its endpoints belong to distinct clusters; and a dissimilar edge is in disagreement with $\mathcal{C}$ if its endpoints belong to the same cluster. The disagreements vector, $\text{dis}$, is a vector indexed by the vertices of $G$ such that the $v$-th coordinate $\text{dis}_v$ equals the weight of all disagreeing edges incident on $v$. The goal is to produce a clustering that minimizes the $\ell_p$ norm of the disagreements vector for $p\geq 1$. We study the $\ell_p$ objective in Correlation Clustering under the following assumption: Every similar edge has weight in the range of $[\alpha\mathbf{w},\mathbf{w}]$ and every dissimilar edge has weight at least $\alpha\mathbf{w}$ (where $\alpha \leq 1$ and $\mathbf{w}>0$ is a scaling parameter). We give an $O\left((\frac{1}{\alpha})^{\frac{1}{2}-\frac{1}{2p}}\cdot \log\frac{1}{\alpha}\right)$ approximation algorithm for this problem. Furthermore, we show an almost matching convex programming integrality gap.

Correlation Clustering with Asymmetric Classification Errors

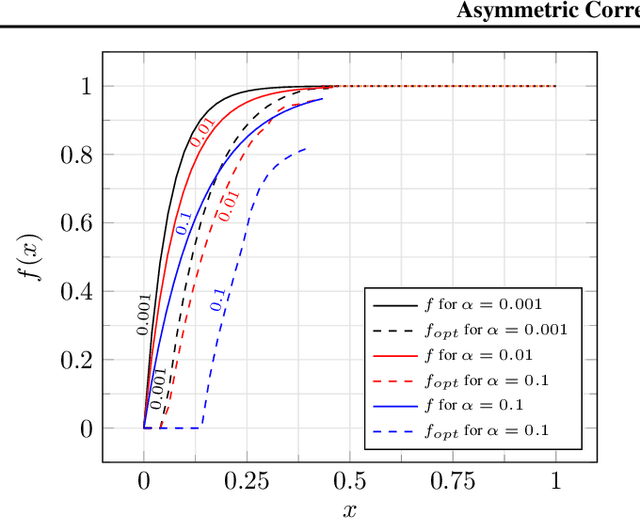
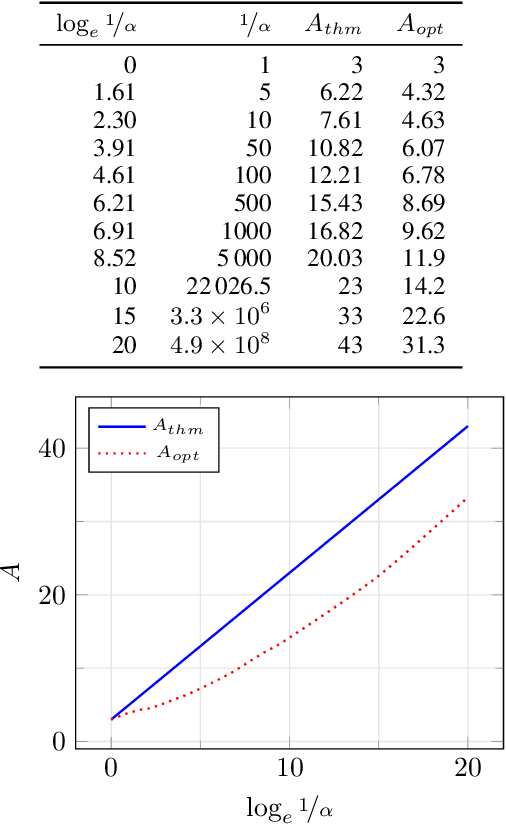
In the Correlation Clustering problem, we are given a weighted graph $G$ with its edges labeled as "similar" or "dissimilar" by a binary classifier. The goal is to produce a clustering that minimizes the weight of "disagreements": the sum of the weights of "similar" edges across clusters and "dissimilar" edges within clusters. We study the correlation clustering problem under the following assumption: Every "similar" edge $e$ has weight $\mathbf{w}_e\in[\alpha \mathbf{w}, \mathbf{w}]$ and every "dissimilar" edge $e$ has weight $\mathbf{w}_e\geq \alpha \mathbf{w}$ (where $\alpha\leq 1$ and $\mathbf{w}>0$ is a scaling parameter). We give a $(3 + 2 \log_e (1/\alpha))$ approximation algorithm for this problem. This assumption captures well the scenario when classification errors are asymmetric. Additionally, we show an asymptotically matching Linear Programming integrality gap of $\Omega(\log 1/\alpha)$.

Near-optimal Algorithms for Explainable k-Medians and k-Means

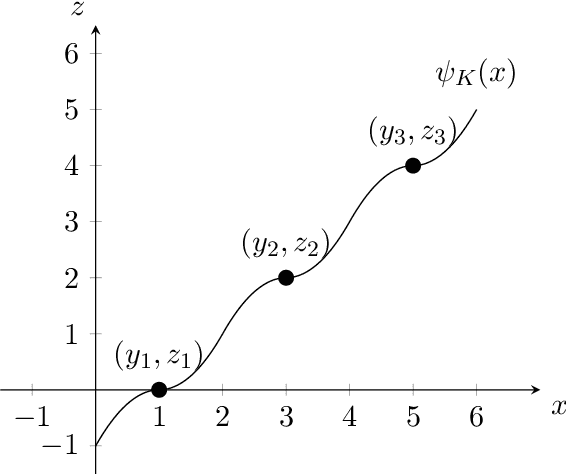
We consider the problem of explainable $k$-medians and $k$-means introduced by Dasgupta, Frost, Moshkovitz, and Rashtchian~(ICML 2020). In this problem, our goal is to find a threshold decision tree that partitions data into $k$ clusters and minimizes the $k$-medians or $k$-means objective. The obtained clustering is easy to interpret because every decision node of a threshold tree splits data based on a single feature into two groups. We propose a new algorithm for this problem which is $\tilde O(\log k)$ competitive with $k$-medians with $\ell_1$ norm and $\tilde O(k)$ competitive with $k$-means. This is an improvement over the previous guarantees of $O(k)$ and $O(k^2)$ by Dasgupta et al (2020). We also provide a new algorithm which is $O(\log^{3/2} k)$ competitive for $k$-medians with $\ell_2$ norm. Our first algorithm is near-optimal: Dasgupta et al (2020) showed a lower bound of $\Omega(\log k)$ for $k$-medians; in this work, we prove a lower bound of $\tilde\Omega(k)$ for $k$-means. We also provide a lower bound of $\Omega(\log k)$ for $k$-medians with $\ell_2$ norm.

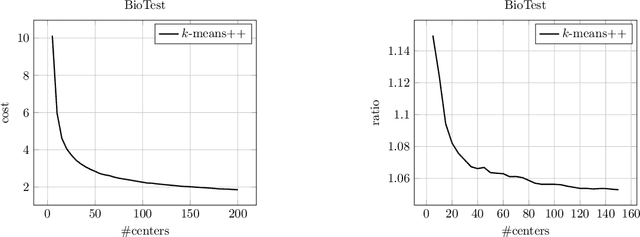
Improved Guarantees for k-means++ and k-means++ Parallel

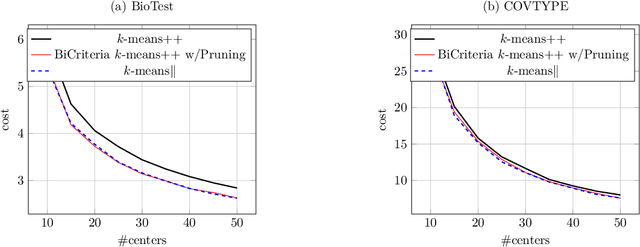
In this paper, we study k-means++ and k-means++ parallel, the two most popular algorithms for the classic k-means clustering problem. We provide novel analyses and show improved approximation and bi-criteria approximation guarantees for k-means++ and k-means++ parallel. Our results give a better theoretical justification for why these algorithms perform extremely well in practice. We also propose a new variant of k-means++ parallel algorithm (Exponential Race k-means++) that has the same approximation guarantees as k-means++.

Nonlinear Dimension Reduction via Outer Bi-Lipschitz Extensions

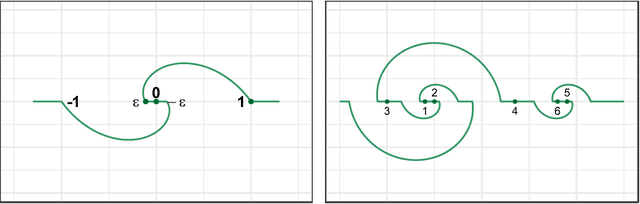
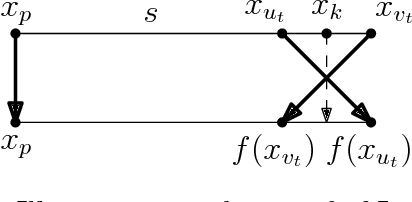
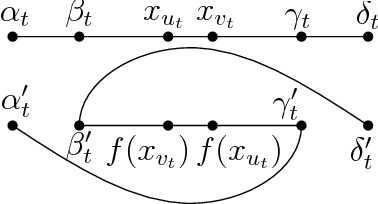
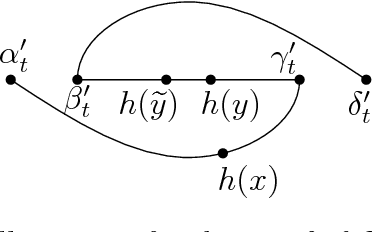
We introduce and study the notion of an outer bi-Lipschitz extension of a map between Euclidean spaces. The notion is a natural analogue of the notion of a Lipschitz extension of a Lipschitz map. We show that for every map $f$ there exists an outer bi-Lipschitz extension $f'$ whose distortion is greater than that of $f$ by at most a constant factor. This result can be seen as a counterpart of the classic Kirszbraun theorem for outer bi-Lipschitz extensions. We also study outer bi-Lipschitz extensions of near-isometric maps and show upper and lower bounds for them. Then, we present applications of our results to prioritized and terminal dimension reduction problems. * We prove a prioritized variant of the Johnson-Lindenstrauss lemma: given a set of points $X\subset \mathbb{R}^d$ of size $N$ and a permutation ("priority ranking") of $X$, there exists an embedding $f$ of $X$ into $\mathbb{R}^{O(\log N)}$ with distortion $O(\log \log N)$ such that the point of rank $j$ has only $O(\log^{3 + \varepsilon} j)$ non-zero coordinates - more specifically, all but the first $O(\log^{3+\varepsilon} j)$ coordinates are equal to $0$; the distortion of $f$ restricted to the first $j$ points (according to the ranking) is at most $O(\log\log j)$. The result makes a progress towards answering an open question by Elkin, Filtser, and Neiman about prioritized dimension reductions. * We prove that given a set $X$ of $N$ points in $\mathbb{R}^d$, there exists a terminal dimension reduction embedding of $\mathbb{R}^d$ into $\mathbb{R}^{d'}$, where $d' = O\left(\frac{\log N}{\varepsilon^4}\right)$, which preserves distances $\|x-y\|$ between points $x\in X$ and $y \in \mathbb{R}^{d}$, up to a multiplicative factor of $1 \pm \varepsilon$. This improves a recent result by Elkin, Filtser, and Neiman. The dimension reductions that we obtain are nonlinear, and this nonlinearity is necessary.

Performance of Johnson-Lindenstrauss Transform for k-Means and k-Medians Clustering

Consider an instance of Euclidean $k$-means or $k$-medians clustering. We show that the cost of the optimal solution is preserved up to a factor of $(1+\varepsilon)$ under a projection onto a random $O(\log(k / \varepsilon) / \varepsilon^2)$-dimensional subspace. Further, the cost of every clustering is preserved within $(1+\varepsilon)$. More generally, our result applies to any dimension reduction map satisfying a mild sub-Gaussian-tail condition. Our bound on the dimension is nearly optimal. Additionally, our result applies to Euclidean $k$-clustering with the distances raised to the $p$-th power for any constant $p$. For $k$-means, our result resolves an open problem posed by Cohen, Elder, Musco, Musco, and Persu (STOC 2015); for $k$-medians, it answers a question raised by Kannan.

Learning Communities in the Presence of Errors

We study the problem of learning communities in the presence of modeling errors and give robust recovery algorithms for the Stochastic Block Model (SBM). This model, which is also known as the Planted Partition Model, is widely used for community detection and graph partitioning in various fields, including machine learning, statistics, and social sciences. Many algorithms exist for learning communities in the Stochastic Block Model, but they do not work well in the presence of errors. In this paper, we initiate the study of robust algorithms for partial recovery in SBM with modeling errors or noise. We consider graphs generated according to the Stochastic Block Model and then modified by an adversary. We allow two types of adversarial errors, Feige---Kilian or monotone errors, and edge outlier errors. Mossel, Neeman and Sly (STOC 2015) posed an open question about whether an almost exact recovery is possible when the adversary is allowed to add $o(n)$ edges. Our work answers this question affirmatively even in the case of $k>2$ communities. We then show that our algorithms work not only when the instances come from SBM, but also work when the instances come from any distribution of graphs that is $\epsilon m$ close to SBM in the Kullback---Leibler divergence. This result also works in the presence of adversarial errors. Finally, we present almost tight lower bounds for two communities.

Correlation Clustering with Noisy Partial Information

In this paper, we propose and study a semi-random model for the Correlation Clustering problem on arbitrary graphs G. We give two approximation algorithms for Correlation Clustering instances from this model. The first algorithm finds a solution of value $(1+ \delta) optcost + O_{\delta}(n\log^3 n)$ with high probability, where $optcost$ is the value of the optimal solution (for every $\delta > 0$). The second algorithm finds the ground truth clustering with an arbitrarily small classification error $\eta$ (under some additional assumptions on the instance).