Computing High-dimensional Confidence Sets for Arbitrary Distributions

We study the problem of learning a high-density region of an arbitrary distribution over $\mathbb{R}^d$. Given a target coverage parameter $\delta$, and sample access to an arbitrary distribution $D$, we want to output a confidence set $S \subset \mathbb{R}^d$ such that $S$ achieves $\delta$ coverage of $D$, i.e., $\mathbb{P}_{y \sim D} \left[ y \in S \right] \ge \delta$, and the volume of $S$ is as small as possible. This is a central problem in high-dimensional statistics with applications in finding confidence sets, uncertainty quantification, and support estimation. In the most general setting, this problem is statistically intractable, so we restrict our attention to competing with sets from a concept class $C$ with bounded VC-dimension. An algorithm is competitive with class $C$ if, given samples from an arbitrary distribution $D$, it outputs in polynomial time a set that achieves $\delta$ coverage of $D$, and whose volume is competitive with the smallest set in $C$ with the required coverage $\delta$. This problem is computationally challenging even in the basic setting when $C$ is the set of all Euclidean balls. Existing algorithms based on coresets find in polynomial time a ball whose volume is $\exp(\tilde{O}( d/ \log d))$-factor competitive with the volume of the best ball. Our main result is an algorithm that finds a confidence set whose volume is $\exp(\tilde{O}(d^{2/3}))$ factor competitive with the optimal ball having the desired coverage. The algorithm is improper (it outputs an ellipsoid). Combined with our computational intractability result for proper learning balls within an $\exp(\tilde{O}(d^{1-o(1)}))$ approximation factor in volume, our results provide an interesting separation between proper and (improper) learning of confidence sets.

Volume Optimality in Conformal Prediction with Structured Prediction Sets

Conformal Prediction is a widely studied technique to construct prediction sets of future observations. Most conformal prediction methods focus on achieving the necessary coverage guarantees, but do not provide formal guarantees on the size (volume) of the prediction sets. We first prove an impossibility of volume optimality where any distribution-free method can only find a trivial solution. We then introduce a new notion of volume optimality by restricting the prediction sets to belong to a set family (of finite VC-dimension), specifically a union of $k$-intervals. Our main contribution is an efficient distribution-free algorithm based on dynamic programming (DP) to find a union of $k$-intervals that is guaranteed for any distribution to have near-optimal volume among all unions of $k$-intervals satisfying the desired coverage property. By adopting the framework of distributional conformal prediction (Chernozhukov et al., 2021), the new DP based conformity score can also be applied to achieve approximate conditional coverage and conditional restricted volume optimality, as long as a reasonable estimator of the conditional CDF is available. While the theoretical results already establish volume-optimality guarantees, they are complemented by experiments that demonstrate that our method can significantly outperform existing methods in many settings.

Verifying Classification with Limited Disclosure

We consider the multi-party classification problem introduced by Dong, Hartline, and Vijayaraghavan (2022) motivated by electronic discovery. In this problem, our goal is to design a protocol that guarantees the requesting party receives nearly all responsive documents while minimizing the disclosure of nonresponsive documents. We develop verification protocols that certify the correctness of a classifier by disclosing a few nonresponsive documents. We introduce a combinatorial notion called the Leave-One-Out dimension of a family of classifiers and show that the number of nonresponsive documents disclosed by our protocol is at most this dimension in the realizable setting, where a perfect classifier exists in this family. For linear classifiers with a margin, we characterize the trade-off between the margin and the number of nonresponsive documents that must be disclosed for verification. Specifically, we establish a trichotomy in this requirement: for $d$ dimensional instances, when the margin exceeds $1/3$, verification can be achieved by revealing only $O(1)$ nonresponsive documents; when the margin is exactly $1/3$, in the worst case, at least $\Omega(d)$ nonresponsive documents must be disclosed; when the margin is smaller than $1/3$, verification requires $\Omega(e^d)$ nonresponsive documents. We believe this result is of independent interest with applications to coding theory and combinatorial geometry. We further extend our protocols to the nonrealizable setting defining an analogous combinatorial quantity robust Leave-One-Out dimension, and to scenarios where the protocol is tolerant to misclassification errors by Alice.

Multi-dimensional Test Design

How should one jointly design tests and the arrangement of agencies to administer these tests (testing procedure)? To answer this question, we analyze a model where a principal must use multiple tests to screen an agent with a multi-dimensional type, knowing that the agent can change his type at a cost. We identify a new tradeoff between setting difficult tests and using a difficult testing procedure. We compare two settings: (1) the agent only misrepresents his type (manipulation) and (2) the agent improves his actual type (investment). Examples include interviews, regulations, and data classification. We show that in the manipulation setting, stringent tests combined with an easy procedure, i.e., offering tests sequentially in a fixed order, is optimal. In contrast, in the investment setting, non-stringent tests with a difficult procedure, i.e., offering tests simultaneously, is optimal; however, under mild conditions offering them sequentially in a random order may be as good. Our results suggest that whether the agent manipulates or invests in his type determines which arrangement of agencies is optimal.

Heterogeneous Multi-agent Multi-armed Bandits on Stochastic Block Models

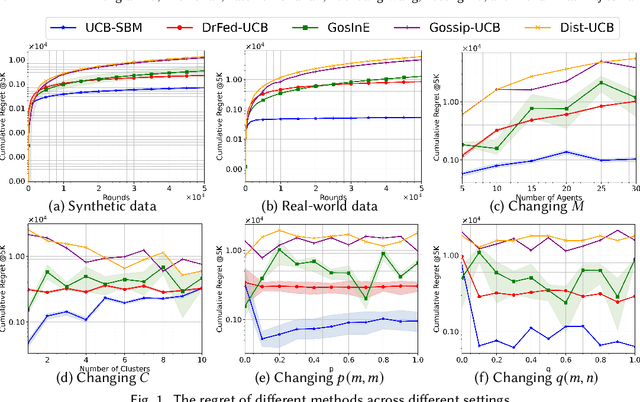
We study a novel heterogeneous multi-agent multi-armed bandit problem with a cluster structure induced by stochastic block models, influencing not only graph topology, but also reward heterogeneity. Specifically, agents are distributed on random graphs based on stochastic block models - a generalized Erdos-Renyi model with heterogeneous edge probabilities: agents are grouped into clusters (known or unknown); edge probabilities for agents within the same cluster differ from those across clusters. In addition, the cluster structure in stochastic block model also determines our heterogeneous rewards. Rewards distributions of the same arm vary across agents in different clusters but remain consistent within a cluster, unifying homogeneous and heterogeneous settings and varying degree of heterogeneity, and rewards are independent samples from these distributions. The objective is to minimize system-wide regret across all agents. To address this, we propose a novel algorithm applicable to both known and unknown cluster settings. The algorithm combines an averaging-based consensus approach with a newly introduced information aggregation and weighting technique, resulting in a UCB-type strategy. It accounts for graph randomness, leverages both intra-cluster (homogeneous) and inter-cluster (heterogeneous) information from rewards and graphs, and incorporates cluster detection for unknown cluster settings. We derive optimal instance-dependent regret upper bounds of order $\log{T}$ under sub-Gaussian rewards. Importantly, our regret bounds capture the degree of heterogeneity in the system (an additional layer of complexity), exhibit smaller constants, scale better for large systems, and impose significantly relaxed assumptions on edge probabilities. In contrast, prior works have not accounted for this refined problem complexity, rely on more stringent assumptions, and exhibit limited scalability.

LiD-FL: Towards List-Decodable Federated Learning

Federated learning is often used in environments with many unverified participants. Therefore, federated learning under adversarial attacks receives significant attention. This paper proposes an algorithmic framework for list-decodable federated learning, where a central server maintains a list of models, with at least one guaranteed to perform well. The framework has no strict restriction on the fraction of honest workers, extending the applicability of Byzantine federated learning to the scenario with more than half adversaries. Under proper assumptions on the loss function, we prove a convergence theorem for our method. Experimental results, including image classification tasks with both convex and non-convex losses, demonstrate that the proposed algorithm can withstand the malicious majority under various attacks.

Error-Tolerant E-Discovery Protocols

We consider the multi-party classification problem introduced by Dong, Hartline, and Vijayaraghavan (2022) in the context of electronic discovery (e-discovery). Based on a request for production from the requesting party, the responding party is required to provide documents that are responsive to the request except for those that are legally privileged. Our goal is to find a protocol that verifies that the responding party sends almost all responsive documents while minimizing the disclosure of non-responsive documents. We provide protocols in the challenging non-realizable setting, where the instance may not be perfectly separated by a linear classifier. We demonstrate empirically that our protocol successfully manages to find almost all relevant documents, while incurring only a small disclosure of non-responsive documents. We complement this with a theoretical analysis of our protocol in the single-dimensional setting, and other experiments on simulated data which suggest that the non-responsive disclosure incurred by our protocol may be unavoidable.

Explainable k-means. Don't be greedy, plant bigger trees!

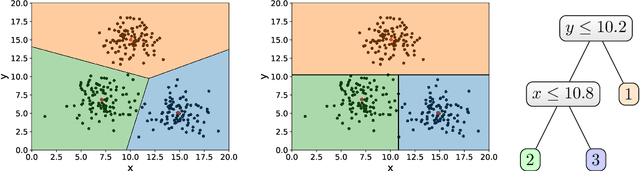
We provide a new bi-criteria $\tilde{O}(\log^2 k)$ competitive algorithm for explainable $k$-means clustering. Explainable $k$-means was recently introduced by Dasgupta, Frost, Moshkovitz, and Rashtchian (ICML 2020). It is described by an easy to interpret and understand (threshold) decision tree or diagram. The cost of the explainable $k$-means clustering equals to the sum of costs of its clusters; and the cost of each cluster equals the sum of squared distances from the points in the cluster to the center of that cluster. Our randomized bi-criteria algorithm constructs a threshold decision tree that partitions the data set into $(1+\delta)k$ clusters (where $\delta\in (0,1)$ is a parameter of the algorithm). The cost of this clustering is at most $\tilde{O}(1/\delta \cdot \log^2 k)$ times the cost of the optimal unconstrained $k$-means clustering. We show that this bound is almost optimal.

Near-optimal Algorithms for Explainable k-Medians and k-Means

We consider the problem of explainable $k$-medians and $k$-means introduced by Dasgupta, Frost, Moshkovitz, and Rashtchian~(ICML 2020). In this problem, our goal is to find a threshold decision tree that partitions data into $k$ clusters and minimizes the $k$-medians or $k$-means objective. The obtained clustering is easy to interpret because every decision node of a threshold tree splits data based on a single feature into two groups. We propose a new algorithm for this problem which is $\tilde O(\log k)$ competitive with $k$-medians with $\ell_1$ norm and $\tilde O(k)$ competitive with $k$-means. This is an improvement over the previous guarantees of $O(k)$ and $O(k^2)$ by Dasgupta et al (2020). We also provide a new algorithm which is $O(\log^{3/2} k)$ competitive for $k$-medians with $\ell_2$ norm. Our first algorithm is near-optimal: Dasgupta et al (2020) showed a lower bound of $\Omega(\log k)$ for $k$-medians; in this work, we prove a lower bound of $\tilde\Omega(k)$ for $k$-means. We also provide a lower bound of $\Omega(\log k)$ for $k$-medians with $\ell_2$ norm.

Improved Guarantees for k-means++ and k-means++ Parallel

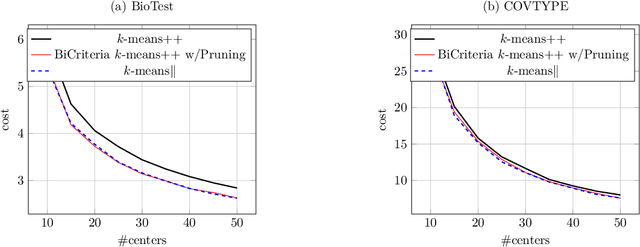
In this paper, we study k-means++ and k-means++ parallel, the two most popular algorithms for the classic k-means clustering problem. We provide novel analyses and show improved approximation and bi-criteria approximation guarantees for k-means++ and k-means++ parallel. Our results give a better theoretical justification for why these algorithms perform extremely well in practice. We also propose a new variant of k-means++ parallel algorithm (Exponential Race k-means++) that has the same approximation guarantees as k-means++.