Linear quadratic control of nonlinear systems with Koopman operator learning and the Nyström method

In this paper, we study how the Koopman operator framework can be combined with kernel methods to effectively control nonlinear dynamical systems. While kernel methods have typically large computational requirements, we show how random subspaces (Nystr\"om approximation) can be used to achieve huge computational savings while preserving accuracy. Our main technical contribution is deriving theoretical guarantees on the effect of the Nystr\"om approximation. More precisely, we study the linear quadratic regulator problem, showing that both the approximated Riccati operator and the regulator objective, for the associated solution of the optimal control problem, converge at the rate $m^{-1/2}$, where $m$ is the random subspace size. Theoretical findings are complemented by numerical experiments corroborating our results.

Efficient Numerical Integration in Reproducing Kernel Hilbert Spaces via Leverage Scores Sampling

In this work we consider the problem of numerical integration, i.e., approximating integrals with respect to a target probability measure using only pointwise evaluations of the integrand. We focus on the setting in which the target distribution is only accessible through a set of $n$ i.i.d. observations, and the integrand belongs to a reproducing kernel Hilbert space. We propose an efficient procedure which exploits a small i.i.d. random subset of $m<n$ samples drawn either uniformly or using approximate leverage scores from the initial observations. Our main result is an upper bound on the approximation error of this procedure for both sampling strategies. It yields sufficient conditions on the subsample size to recover the standard (optimal) $n^{-1/2}$ rate while reducing drastically the number of functions evaluations, and thus the overall computational cost. Moreover, we obtain rates with respect to the number $m$ of evaluations of the integrand which adapt to its smoothness, and match known optimal rates for instance for Sobolev spaces. We illustrate our theoretical findings with numerical experiments on real datasets, which highlight the attractive efficiency-accuracy tradeoff of our method compared to existing randomized and greedy quadrature methods. We note that, the problem of numerical integration in RKHS amounts to designing a discrete approximation of the kernel mean embedding of the target distribution. As a consequence, direct applications of our results also include the efficient computation of maximum mean discrepancies between distributions and the design of efficient kernel-based tests.

Estimating Koopman operators with sketching to provably learn large scale dynamical systems

The theory of Koopman operators allows to deploy non-parametric machine learning algorithms to predict and analyze complex dynamical systems. Estimators such as principal component regression (PCR) or reduced rank regression (RRR) in kernel spaces can be shown to provably learn Koopman operators from finite empirical observations of the system's time evolution. Scaling these approaches to very long trajectories is a challenge and requires introducing suitable approximations to make computations feasible. In this paper, we boost the efficiency of different kernel-based Koopman operator estimators using random projections (sketching). We derive, implement and test the new "sketched" estimators with extensive experiments on synthetic and large-scale molecular dynamics datasets. Further, we establish non asymptotic error bounds giving a sharp characterization of the trade-offs between statistical learning rates and computational efficiency. Our empirical and theoretical analysis shows that the proposed estimators provide a sound and efficient way to learn large scale dynamical systems. In particular our experiments indicate that the proposed estimators retain the same accuracy of PCR or RRR, while being much faster.

M$^2$M: A general method to perform various data analysis tasks from a differentially private sketch

Differential privacy is the standard privacy definition for performing analyses over sensitive data. Yet, its privacy budget bounds the number of tasks an analyst can perform with reasonable accuracy, which makes it challenging to deploy in practice. This can be alleviated by private sketching, where the dataset is compressed into a single noisy sketch vector which can be shared with the analysts and used to perform arbitrarily many analyses. However, the algorithms to perform specific tasks from sketches must be developed on a case-by-case basis, which is a major impediment to their use. In this paper, we introduce the generic moment-to-moment (M$^2$M) method to perform a wide range of data exploration tasks from a single private sketch. Among other things, this method can be used to estimate empirical moments of attributes, the covariance matrix, counting queries (including histograms), and regression models. Our method treats the sketching mechanism as a black-box operation, and can thus be applied to a wide variety of sketches from the literature, widening their ranges of applications without further engineering or privacy loss, and removing some of the technical barriers to the wider adoption of sketches for data exploration under differential privacy. We validate our method with data exploration tasks on artificial and real-world data, and show that it can be used to reliably estimate statistics and train classification models from private sketches.

Nyström Kernel Mean Embeddings

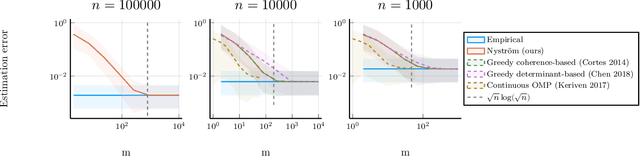
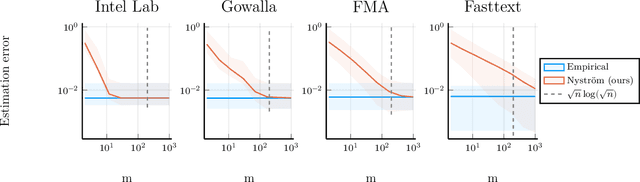
Kernel mean embeddings are a powerful tool to represent probability distributions over arbitrary spaces as single points in a Hilbert space. Yet, the cost of computing and storing such embeddings prohibits their direct use in large-scale settings. We propose an efficient approximation procedure based on the Nystr\"om method, which exploits a small random subset of the dataset. Our main result is an upper bound on the approximation error of this procedure. It yields sufficient conditions on the subsample size to obtain the standard $n^{-1/2}$ rate while reducing computational costs. We discuss applications of this result for the approximation of the maximum mean discrepancy and quadrature rules, and illustrate our theoretical findings with numerical experiments.

Mean Nyström Embeddings for Adaptive Compressive Learning

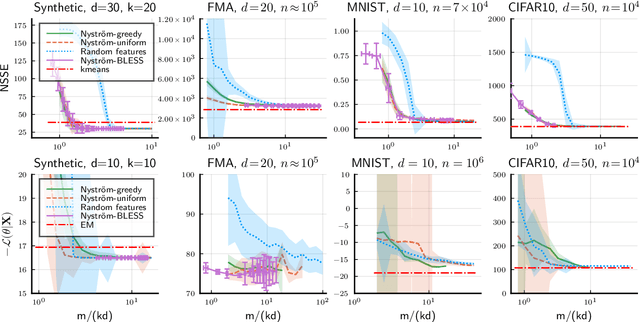
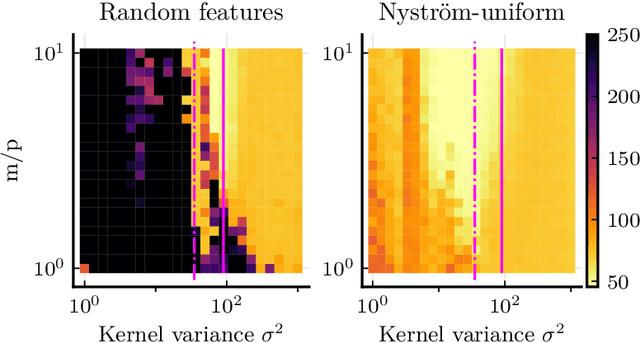
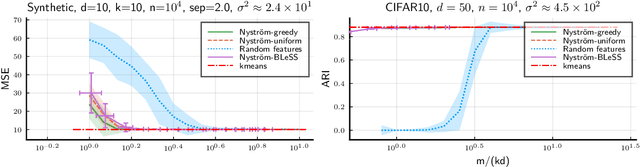
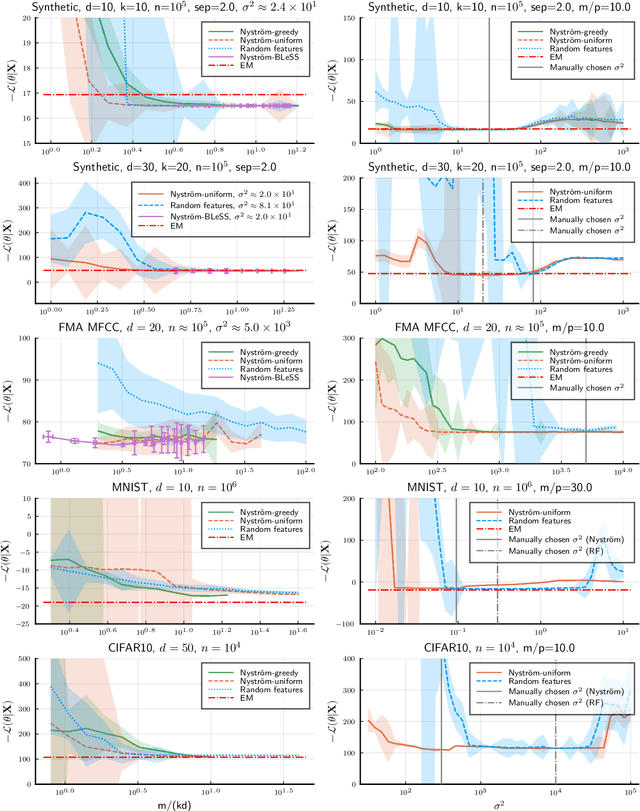
Compressive learning is an approach to efficient large scale learning based on sketching an entire dataset to a single mean embedding (the sketch), i.e. a vector of generalized moments. The learning task is then approximately solved as an inverse problem using an adapted parametric model. Previous works in this context have focused on sketches obtained by averaging random features, that while universal can be poorly adapted to the problem at hand. In this paper, we propose and study the idea of performing sketching based on data-dependent Nystr\"om approximation. From a theoretical perspective we prove that the excess risk can be controlled under a geometric assumption relating the parametric model used to learn from the sketch and the covariance operator associated to the task at hand. Empirically, we show for k-means clustering and Gaussian modeling that for a fixed sketch size, Nystr\"om sketches indeed outperform those built with random features.

Sketching Datasets for Large-Scale Learning (long version)

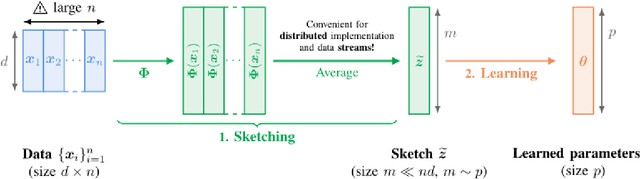
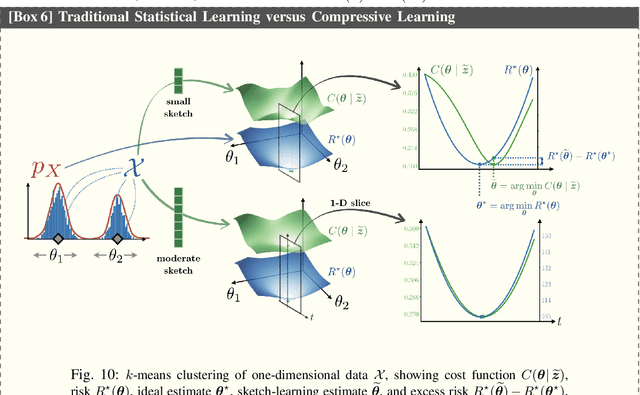
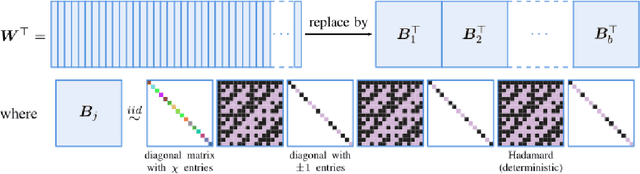
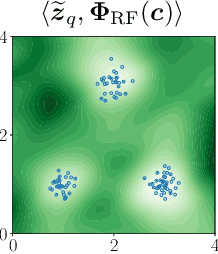
This article considers "sketched learning," or "compressive learning," an approach to large-scale machine learning where datasets are massively compressed before learning (e.g., clustering, classification, or regression) is performed. In particular, a "sketch" is first constructed by computing carefully chosen nonlinear random features (e.g., random Fourier features) and averaging them over the whole dataset. Parameters are then learned from the sketch, without access to the original dataset. This article surveys the current state-of-the-art in sketched learning, including the main concepts and algorithms, their connections with established signal-processing methods, existing theoretical guarantees---on both information preservation and privacy preservation, and important open problems.