Efficient Numerical Integration in Reproducing Kernel Hilbert Spaces via Leverage Scores Sampling

In this work we consider the problem of numerical integration, i.e., approximating integrals with respect to a target probability measure using only pointwise evaluations of the integrand. We focus on the setting in which the target distribution is only accessible through a set of $n$ i.i.d. observations, and the integrand belongs to a reproducing kernel Hilbert space. We propose an efficient procedure which exploits a small i.i.d. random subset of $m<n$ samples drawn either uniformly or using approximate leverage scores from the initial observations. Our main result is an upper bound on the approximation error of this procedure for both sampling strategies. It yields sufficient conditions on the subsample size to recover the standard (optimal) $n^{-1/2}$ rate while reducing drastically the number of functions evaluations, and thus the overall computational cost. Moreover, we obtain rates with respect to the number $m$ of evaluations of the integrand which adapt to its smoothness, and match known optimal rates for instance for Sobolev spaces. We illustrate our theoretical findings with numerical experiments on real datasets, which highlight the attractive efficiency-accuracy tradeoff of our method compared to existing randomized and greedy quadrature methods. We note that, the problem of numerical integration in RKHS amounts to designing a discrete approximation of the kernel mean embedding of the target distribution. As a consequence, direct applications of our results also include the efficient computation of maximum mean discrepancies between distributions and the design of efficient kernel-based tests.

Nyström Kernel Mean Embeddings

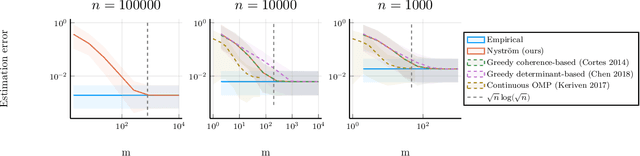
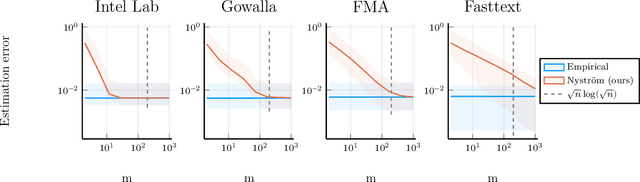
Kernel mean embeddings are a powerful tool to represent probability distributions over arbitrary spaces as single points in a Hilbert space. Yet, the cost of computing and storing such embeddings prohibits their direct use in large-scale settings. We propose an efficient approximation procedure based on the Nystr\"om method, which exploits a small random subset of the dataset. Our main result is an upper bound on the approximation error of this procedure. It yields sufficient conditions on the subsample size to obtain the standard $n^{-1/2}$ rate while reducing computational costs. We discuss applications of this result for the approximation of the maximum mean discrepancy and quadrature rules, and illustrate our theoretical findings with numerical experiments.

Classification with abstention but without disparities

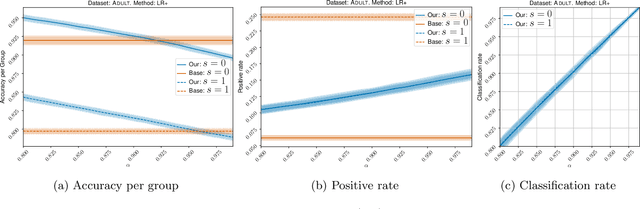
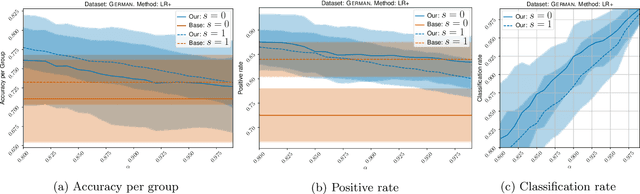
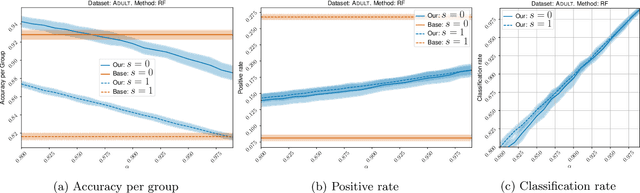
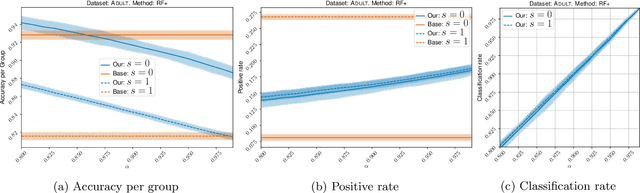
Classification with abstention has gained a lot of attention in recent years as it allows to incorporate human decision-makers in the process. Yet, abstention can potentially amplify disparities and lead to discriminatory predictions. The goal of this work is to build a general purpose classification algorithm, which is able to abstain from prediction, while avoiding disparate impact. We formalize this problem as risk minimization under fairness and abstention constraints for which we derive the form of the optimal classifier. Building on this result, we propose a post-processing classification algorithm, which is able to modify any off-the-shelf score-based classifier using only unlabeled sample. We establish finite sample risk, fairness, and abstention guarantees for the proposed algorithm. In particular, it is shown that fairness and abstention constraints can be achieved independently from the initial classifier as long as sufficiently many unlabeled data is available. The risk guarantee is established in terms of the quality of the initial classifier. Our post-processing scheme reduces to a sparse linear program allowing for an efficient implementation, which we provide. Finally, we validate our method empirically showing that moderate abstention rates allow to bypass the risk-fairness trade-off.

An example of prediction which complies with Demographic Parity and equalizes group-wise risks in the context of regression

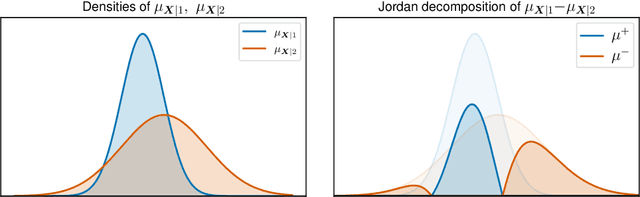
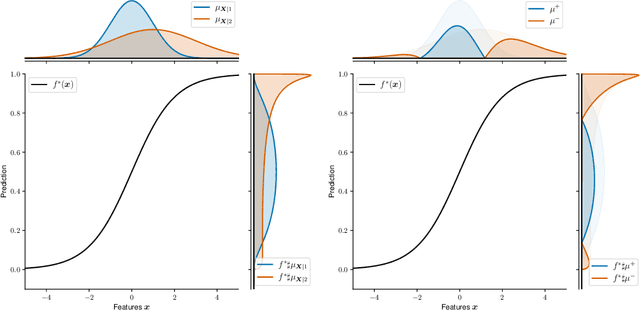
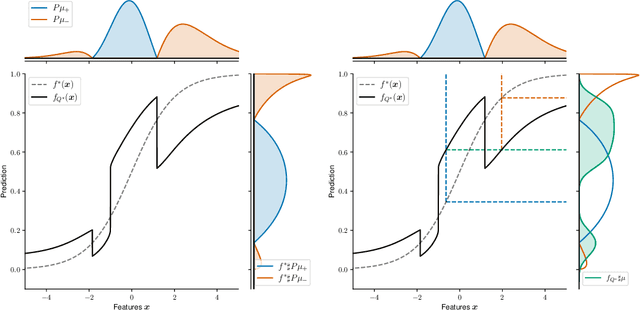
Let $(X, S, Y) \in \mathbb{R}^p \times \{1, 2\} \times \mathbb{R}$ be a triplet following some joint distribution $\mathbb{P}$ with feature vector $X$, sensitive attribute $S$ , and target variable $Y$. The Bayes optimal prediction $f^*$ which does not produce Disparate Treatment is defined as $f^*(x) = \mathbb{E}[Y | X = x]$. We provide a non-trivial example of a prediction $x \to f(x)$ which satisfies two common group-fairness notions: Demographic Parity \begin{align} (f(X) | S = 1) &\stackrel{d}{=} (f(X) | S = 2) \end{align} and Equal Group-Wise Risks \begin{align} \mathbb{E}[(f^*(X) - f(X))^2 | S = 1] = \mathbb{E}[(f^*(X) - f(X))^2 | S = 2]. \end{align} To the best of our knowledge this is the first explicit construction of a non-constant predictor satisfying the above. We discuss several implications of this result on better understanding of mathematical notions of algorithmic fairness.

Statistical guarantees for generative models without domination

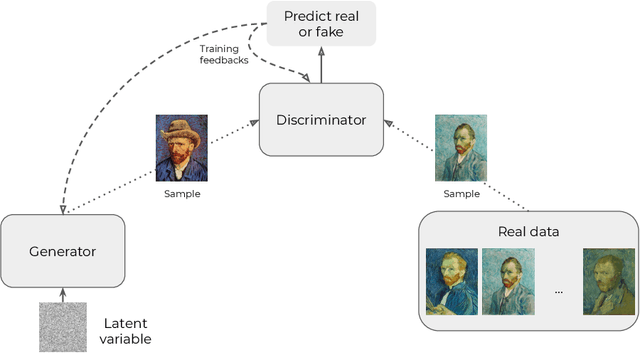
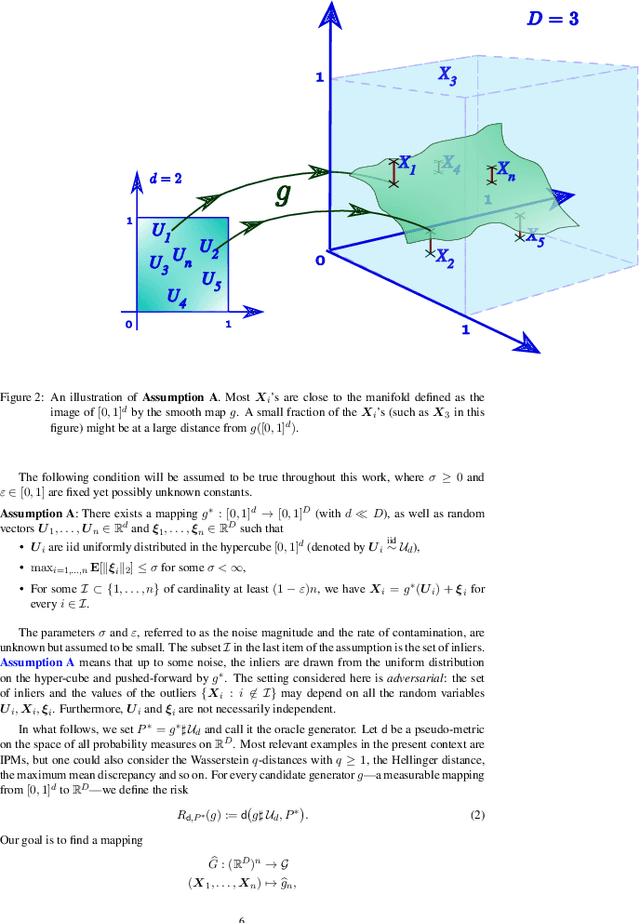
In this paper, we introduce a convenient framework for studying (adversarial) generative models from a statistical perspective. It consists in modeling the generative device as a smooth transformation of the unit hypercube of a dimension that is much smaller than that of the ambient space and measuring the quality of the generative model by means of an integral probability metric. In the particular case of integral probability metric defined through a smoothness class, we establish a risk bound quantifying the role of various parameters. In particular, it clearly shows the impact of dimension reduction on the error of the generative model.

Bounding the expectation of the supremum of empirical processes indexed by Hölder classes

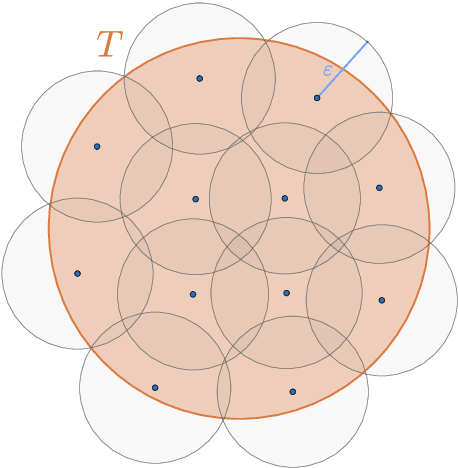
We obtain upper bounds on the expectation of the supremum of empirical processes indexed by H\"older classes of any smoothness and for any distribution supported on a bounded set. Another way to see it is from the point of view of integral probability metrics (IPM), a class of metrics on the space of probability measures: our rates quantify how quickly the empirical measure obtained from $n$ independent samples from a probability measure $P$ approaches $P$ with respect to the IPM indexed by H\"older classes. As an extremal case we recover the known rates for the Wassertein-1 distance.

A nonasymptotic law of iterated logarithm for robust online estimators

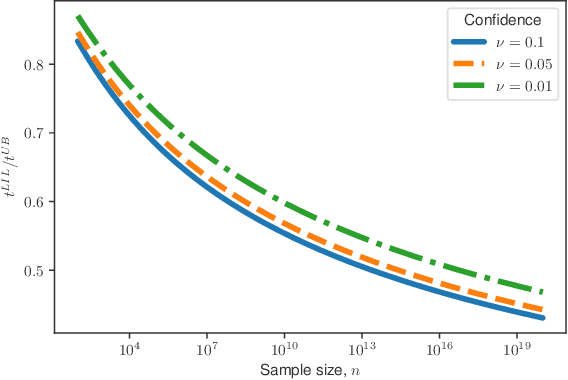
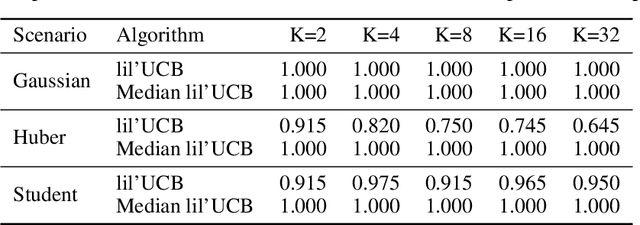
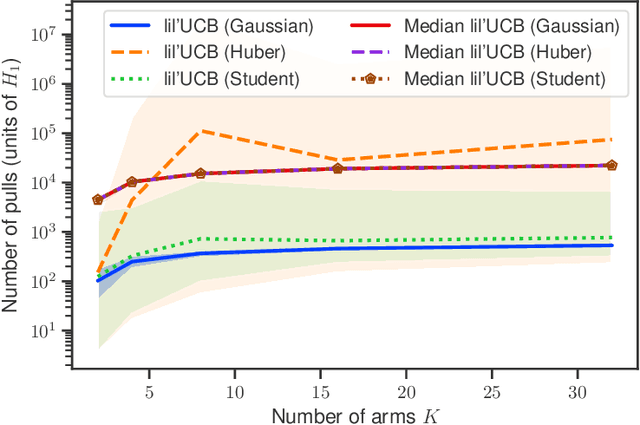
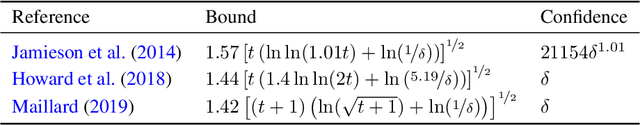
In this paper, we provide tight deviation bounds for M-estimators, which are valid with a prescribed probability for every sample size. M-estimators are ubiquitous in machine learning and statistical learning theory. They are used both for defining prediction strategies and for evaluating their precision. Our deviation bounds can be seen as a non-asymptotic version of the law of iterated logarithm. They are established under general assumptions such as Lipschitz continuity of the loss function and (local) curvature of the population risk. These conditions are satisfied for most examples used in machine learning, including those that are known to be robust to outliers and to heavy tailed distributions. To further highlight the scope of applicability of the obtained results, a new algorithm, with provably optimal theoretical guarantees, for the best arm identification in a stochastic multi-arm bandit setting is presented. Numerical experiments illustrating the validity of the algorithm are reported.