Learning convolution operators on compact Abelian groups

We consider the problem of learning convolution operators associated to compact Abelian groups. We study a regularization-based approach and provide corresponding learning guarantees, discussing natural regularity condition on the convolution kernel. More precisely, we assume the convolution kernel is a function in a translation invariant Hilbert space and analyze a natural ridge regression (RR) estimator. Building on existing results for RR, we characterize the accuracy of the estimator in terms of finite sample bounds. Interestingly, regularity assumptions which are classical in the analysis of RR, have a novel and natural interpretation in terms of space/frequency localization. Theoretical results are illustrated by numerical simulations.

Learning sparsity-promoting regularizers for linear inverse problems

This paper introduces a novel approach to learning sparsity-promoting regularizers for solving linear inverse problems. We develop a bilevel optimization framework to select an optimal synthesis operator, denoted as $B$, which regularizes the inverse problem while promoting sparsity in the solution. The method leverages statistical properties of the underlying data and incorporates prior knowledge through the choice of $B$. We establish the well-posedness of the optimization problem, provide theoretical guarantees for the learning process, and present sample complexity bounds. The approach is demonstrated through examples, including compact perturbations of a known operator and the problem of learning the mother wavelet, showcasing its flexibility in incorporating prior knowledge into the regularization framework. This work extends previous efforts in Tikhonov regularization by addressing non-differentiable norms and proposing a data-driven approach for sparse regularization in infinite dimensions.

Neural reproducing kernel Banach spaces and representer theorems for deep networks

Studying the function spaces defined by neural networks helps to understand the corresponding learning models and their inductive bias. While in some limits neural networks correspond to function spaces that are reproducing kernel Hilbert spaces, these regimes do not capture the properties of the networks used in practice. In contrast, in this paper we show that deep neural networks define suitable reproducing kernel Banach spaces. These spaces are equipped with norms that enforce a form of sparsity, enabling them to adapt to potential latent structures within the input data and their representations. In particular, leveraging the theory of reproducing kernel Banach spaces, combined with variational results, we derive representer theorems that justify the finite architectures commonly employed in applications. Our study extends analogous results for shallow networks and can be seen as a step towards considering more practically plausible neural architectures.

Efficient Numerical Integration in Reproducing Kernel Hilbert Spaces via Leverage Scores Sampling

In this work we consider the problem of numerical integration, i.e., approximating integrals with respect to a target probability measure using only pointwise evaluations of the integrand. We focus on the setting in which the target distribution is only accessible through a set of $n$ i.i.d. observations, and the integrand belongs to a reproducing kernel Hilbert space. We propose an efficient procedure which exploits a small i.i.d. random subset of $m<n$ samples drawn either uniformly or using approximate leverage scores from the initial observations. Our main result is an upper bound on the approximation error of this procedure for both sampling strategies. It yields sufficient conditions on the subsample size to recover the standard (optimal) $n^{-1/2}$ rate while reducing drastically the number of functions evaluations, and thus the overall computational cost. Moreover, we obtain rates with respect to the number $m$ of evaluations of the integrand which adapt to its smoothness, and match known optimal rates for instance for Sobolev spaces. We illustrate our theoretical findings with numerical experiments on real datasets, which highlight the attractive efficiency-accuracy tradeoff of our method compared to existing randomized and greedy quadrature methods. We note that, the problem of numerical integration in RKHS amounts to designing a discrete approximation of the kernel mean embedding of the target distribution. As a consequence, direct applications of our results also include the efficient computation of maximum mean discrepancies between distributions and the design of efficient kernel-based tests.

Regularized ERM on random subspaces

We study a natural extension of classical empirical risk minimization, where the hypothesis space is a random subspace of a given space. In particular, we consider possibly data dependent subspaces spanned by a random subset of the data, recovering as a special case Nystrom approaches for kernel methods. Considering random subspaces naturally leads to computational savings, but the question is whether the corresponding learning accuracy is degraded. These statistical-computational tradeoffs have been recently explored for the least squares loss and self-concordant loss functions, such as the logistic loss. Here, we work to extend these results to convex Lipschitz loss functions, that might not be smooth, such as the hinge loss used in support vector machines. This unified analysis requires developing new proofs, that use different technical tools, such as sub-gaussian inputs, to achieve fast rates. Our main results show the existence of different settings, depending on how hard the learning problem is, for which computational efficiency can be improved with no loss in performance.

Multiclass learning with margin: exponential rates with no bias-variance trade-off

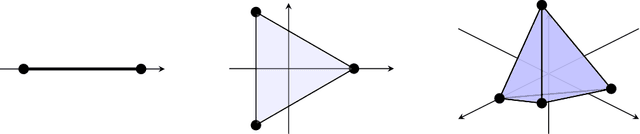
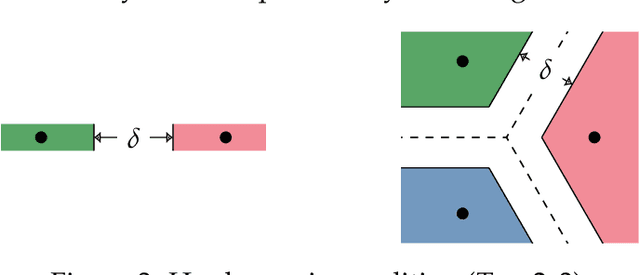
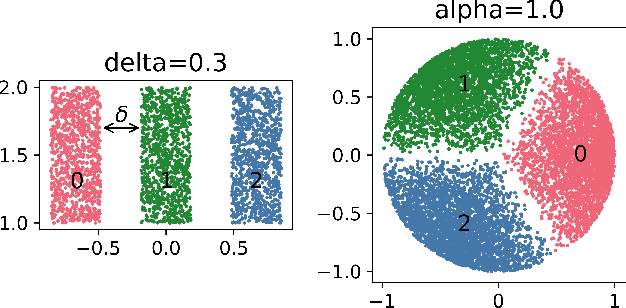
We study the behavior of error bounds for multiclass classification under suitable margin conditions. For a wide variety of methods we prove that the classification error under a hard-margin condition decreases exponentially fast without any bias-variance trade-off. Different convergence rates can be obtained in correspondence of different margin assumptions. With a self-contained and instructive analysis we are able to generalize known results from the binary to the multiclass setting.

Efficient Hyperparameter Tuning for Large Scale Kernel Ridge Regression

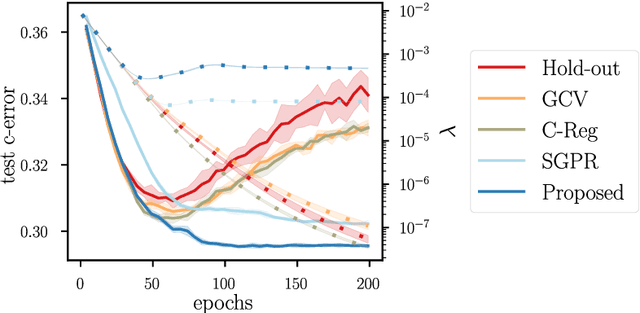
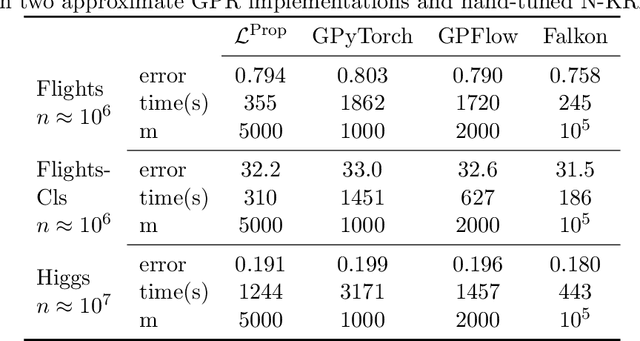
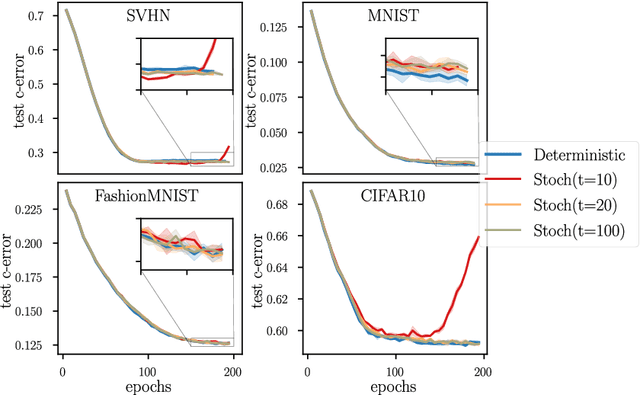
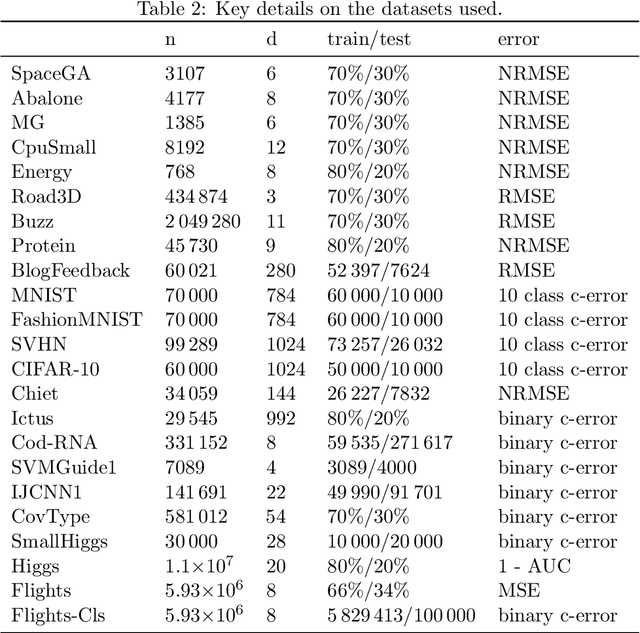
Kernel methods provide a principled approach to nonparametric learning. While their basic implementations scale poorly to large problems, recent advances showed that approximate solvers can efficiently handle massive datasets. A shortcoming of these solutions is that hyperparameter tuning is not taken care of, and left for the user to perform. Hyperparameters are crucial in practice and the lack of automated tuning greatly hinders efficiency and usability. In this paper, we work to fill in this gap focusing on kernel ridge regression based on the Nystr\"om approximation. After reviewing and contrasting a number of hyperparameter tuning strategies, we propose a complexity regularization criterion based on a data dependent penalty, and discuss its efficient optimization. Then, we proceed to a careful and extensive empirical evaluation highlighting strengths and weaknesses of the different tuning strategies. Our analysis shows the benefit of the proposed approach, that we hence incorporate in a library for large scale kernel methods to derive adaptively tuned solutions.

Mean Nyström Embeddings for Adaptive Compressive Learning

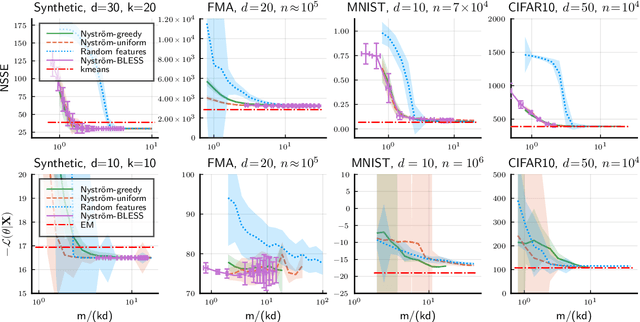
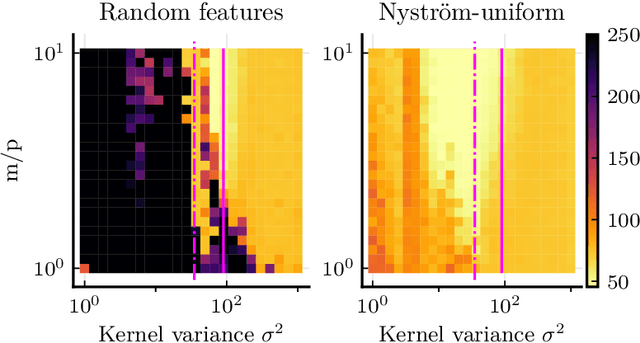
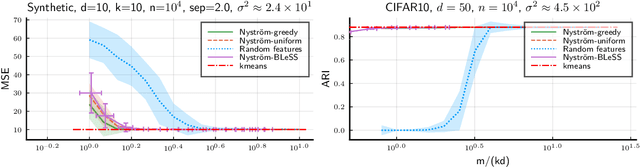
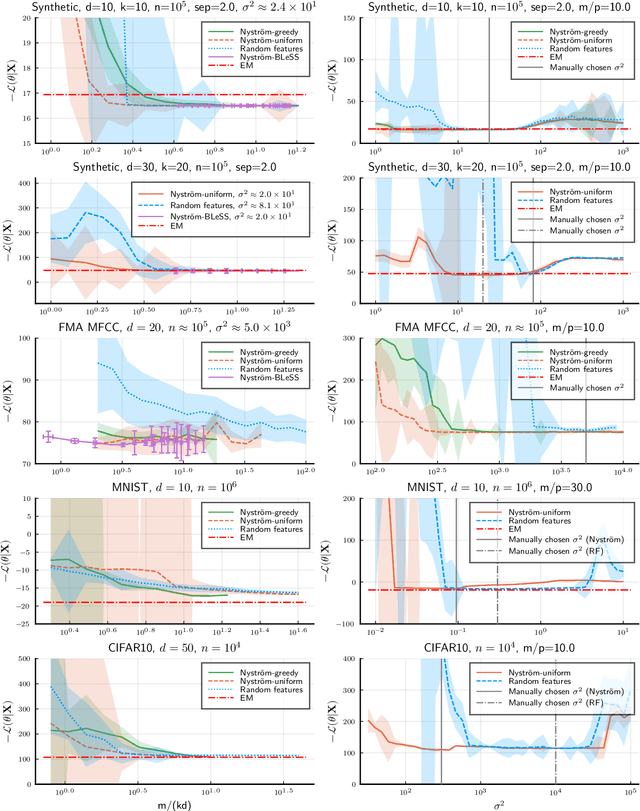
Compressive learning is an approach to efficient large scale learning based on sketching an entire dataset to a single mean embedding (the sketch), i.e. a vector of generalized moments. The learning task is then approximately solved as an inverse problem using an adapted parametric model. Previous works in this context have focused on sketches obtained by averaging random features, that while universal can be poorly adapted to the problem at hand. In this paper, we propose and study the idea of performing sketching based on data-dependent Nystr\"om approximation. From a theoretical perspective we prove that the excess risk can be controlled under a geometric assumption relating the parametric model used to learn from the sketch and the covariance operator associated to the task at hand. Empirically, we show for k-means clustering and Gaussian modeling that for a fixed sketch size, Nystr\"om sketches indeed outperform those built with random features.

Understanding neural networks with reproducing kernel Banach spaces

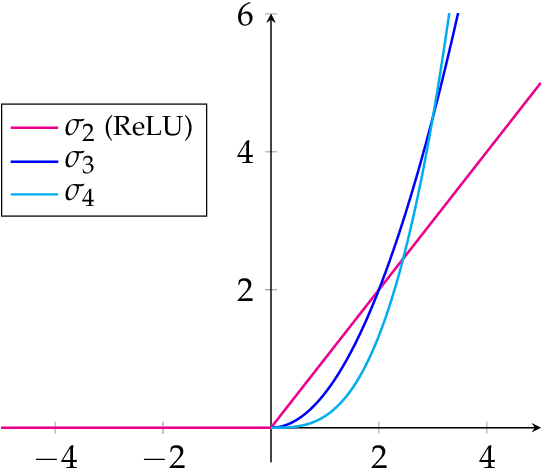
Characterizing the function spaces corresponding to neural networks can provide a way to understand their properties. In this paper we discuss how the theory of reproducing kernel Banach spaces can be used to tackle this challenge. In particular, we prove a representer theorem for a wide class of reproducing kernel Banach spaces that admit a suitable integral representation and include one hidden layer neural networks of possibly infinite width. Further, we show that, for a suitable class of ReLU activation functions, the norm in the corresponding reproducing kernel Banach space can be characterized in terms of the inverse Radon transform of a bounded real measure, with norm given by the total variation norm of the measure. Our analysis simplifies and extends recent results in [34,29,30].

Learning the optimal regularizer for inverse problems

In this work, we consider the linear inverse problem $y=Ax+\epsilon$, where $A\colon X\to Y$ is a known linear operator between the separable Hilbert spaces $X$ and $Y$, $x$ is a random variable in $X$ and $\epsilon$ is a zero-mean random process in $Y$. This setting covers several inverse problems in imaging including denoising, deblurring, and X-ray tomography. Within the classical framework of regularization, we focus on the case where the regularization functional is not given a priori but learned from data. Our first result is a characterization of the optimal generalized Tikhonov regularizer, with respect to the mean squared error. We find that it is completely independent of the forward operator $A$ and depends only on the mean and covariance of $x$. Then, we consider the problem of learning the regularizer from a finite training set in two different frameworks: one supervised, based on samples of both $x$ and $y$, and one unsupervised, based only on samples of $x$. In both cases, we prove generalization bounds, under some weak assumptions on the distribution of $x$ and $\epsilon$, including the case of sub-Gaussian variables. Our bounds hold in infinite-dimensional spaces, thereby showing that finer and finer discretizations do not make this learning problem harder. The results are validated through numerical simulations.