Node Regression on Latent Position Random Graphs via Local Averaging

Node regression consists in predicting the value of a graph label at a node, given observations at the other nodes. To gain some insight into the performance of various estimators for this task, we perform a theoretical study in a context where the graph is random. Specifically, we assume that the graph is generated by a Latent Position Model, where each node of the graph has a latent position, and the probability that two nodes are connected depend on the distance between the latent positions of the two nodes. In this context, we begin by studying the simplest possible estimator for graph regression, which consists in averaging the value of the label at all neighboring nodes. We show that in Latent Position Models this estimator tends to a Nadaraya Watson estimator in the latent space, and that its rate of convergence is in fact the same. One issue with this standard estimator is that it averages over a region consisting of all neighbors of a node, and that depending on the graph model this may be too much or too little. An alternative consists in first estimating the true distances between the latent positions, then injecting these estimated distances into a classical Nadaraya Watson estimator. This enables averaging in regions either smaller or larger than the typical graph neighborhood. We show that this method can achieve standard nonparametric rates in certain instances even when the graph neighborhood is too large or too small.

Graph Coarsening with Message-Passing Guarantees

Graph coarsening aims to reduce the size of a large graph while preserving some of its key properties, which has been used in many applications to reduce computational load and memory footprint. For instance, in graph machine learning, training Graph Neural Networks (GNNs) on coarsened graphs leads to drastic savings in time and memory. However, GNNs rely on the Message-Passing (MP) paradigm, and classical spectral preservation guarantees for graph coarsening do not directly lead to theoretical guarantees when performing naive message-passing on the coarsened graph. In this work, we propose a new message-passing operation specific to coarsened graphs, which exhibit theoretical guarantees on the preservation of the propagated signal. Interestingly, and in a sharp departure from previous proposals, this operation on coarsened graphs is oriented, even when the original graph is undirected. We conduct node classification tasks on synthetic and real data and observe improved results compared to performing naive message-passing on the coarsened graph.

What functions can Graph Neural Networks compute on random graphs? The role of Positional Encoding

We aim to deepen the theoretical understanding of Graph Neural Networks (GNNs) on large graphs, with a focus on their expressive power. Existing analyses relate this notion to the graph isomorphism problem, which is mostly relevant for graphs of small sizes, or studied graph classification or regression tasks, while prediction tasks on nodes are far more relevant on large graphs. Recently, several works showed that, on very general random graphs models, GNNs converge to certains functions as the number of nodes grows. In this paper, we provide a more complete and intuitive description of the function space generated by equivariant GNNs for node-tasks, through general notions of convergence that encompass several previous examples. We emphasize the role of input node features, and study the impact of node Positional Encodings (PEs), a recent line of work that has been shown to yield state-of-the-art results in practice. Through the study of several examples of PEs on large random graphs, we extend previously known universality results to significantly more general models. Our theoretical results hint at some normalization tricks, which is shown numerically to have a positive impact on GNN generalization on synthetic and real data. Our proofs contain new concentration inequalities of independent interest.

Convergence of Message Passing Graph Neural Networks with Generic Aggregation On Large Random Graphs

We study the convergence of message passing graph neural networks on random graph models to their continuous counterpart as the number of nodes tends to infinity. Until now, this convergence was only known for architectures with aggregation functions in the form of degree-normalized means. We extend such results to a very large class of aggregation functions, that encompasses all classically used message passing graph neural networks, such as attention-based mesage passing or max convolutional message passing on top of (degree-normalized) convolutional message passing. Under mild assumptions, we give non asymptotic bounds with high probability to quantify this convergence. Our main result is based on the McDiarmid inequality. Interestingly, we treat the case where the aggregation is a coordinate-wise maximum separately, at it necessitates a very different proof technique and yields a qualitatively different convergence rate.

Gradient scarcity with Bilevel Optimization for Graph Learning

A common issue in graph learning under the semi-supervised setting is referred to as gradient scarcity. That is, learning graphs by minimizing a loss on a subset of nodes causes edges between unlabelled nodes that are far from labelled ones to receive zero gradients. The phenomenon was first described when optimizing the graph and the weights of a Graph Neural Network (GCN) with a joint optimization algorithm. In this work, we give a precise mathematical characterization of this phenomenon, and prove that it also emerges in bilevel optimization, where additional dependency exists between the parameters of the problem. While for GCNs gradient scarcity occurs due to their finite receptive field, we show that it also occurs with the Laplacian regularization model, in the sense that gradients amplitude decreases exponentially with distance to labelled nodes. To alleviate this issue, we study several solutions: we propose to resort to latent graph learning using a Graph-to-Graph model (G2G), graph regularization to impose a prior structure on the graph, or optimizing on a larger graph than the original one with a reduced diameter. Our experiments on synthetic and real datasets validate our analysis and prove the efficiency of the proposed solutions.

Stability of Entropic Wasserstein Barycenters and application to random geometric graphs

As interest in graph data has grown in recent years, the computation of various geometric tools has become essential. In some area such as mesh processing, they often rely on the computation of geodesics and shortest paths in discretized manifolds. A recent example of such a tool is the computation of Wasserstein barycenters (WB), a very general notion of barycenters derived from the theory of Optimal Transport, and their entropic-regularized variant. In this paper, we examine how WBs on discretized meshes relate to the geometry of the underlying manifold. We first provide a generic stability result with respect to the input cost matrices. We then apply this result to random geometric graphs on manifolds, whose shortest paths converge to geodesics, hence proving the consistency of WBs computed on discretized shapes.

Not too little, not too much: a theoretical analysis of graph smoothing

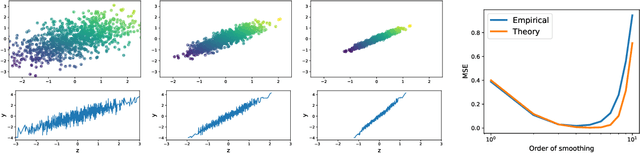
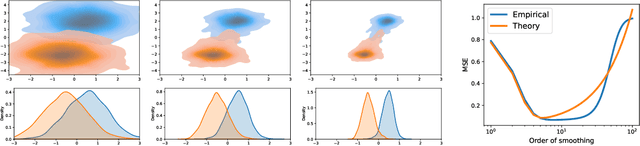
We analyze graph smoothing with \emph{mean aggregation}, where each node successively receives the average of the features of its neighbors. Indeed, it has quickly been observed that Graph Neural Networks (GNNs), which generally follow some variant of Message-Passing (MP) with repeated aggregation, may be subject to the \emph{oversmoothing} phenomenon: by performing too many rounds of MP, the node features tend to converge to a non-informative limit. In the case of mean aggregation, for connected graphs, the node features become constant across the whole graph. At the other end of the spectrum, it is intuitively obvious that \emph{some} MP rounds are necessary, but existing analyses do not exhibit both phenomena at once: beneficial ``finite'' smoothing and oversmoothing in the limit. In this paper, we consider simplified linear GNNs, and rigorously analyze two examples for which a finite number of mean aggregation steps provably improves the learning performance, before oversmoothing kicks in. We consider a latent space random graph model, where node features are partial observations of the latent variables and the graph contains pairwise relationships between them. We show that graph smoothing restores some of the lost information, up to a certain point, by two phenomenon: graph smoothing shrinks non-principal directions in the data faster than principal ones, which is useful for regression, and shrinks nodes within communities faster than they collapse together, which improves classification.

Entropic Optimal Transport in Random Graphs

In graph analysis, a classic task consists in computing similarity measures between (groups of) nodes. In latent space random graphs, nodes are associated to unknown latent variables. One may then seek to compute distances directly in the latent space, using only the graph structure. In this paper, we show that it is possible to consistently estimate entropic-regularized Optimal Transport (OT) distances between groups of nodes in the latent space. We provide a general stability result for entropic OT with respect to perturbations of the cost matrix. We then apply it to several examples of random graphs, such as graphons or $\epsilon$-graphs on manifolds. Along the way, we prove new concentration results for the so-called Universal Singular Value Thresholding estimator, and for the estimation of geodesic distances on a manifold.

Supervised learning of analysis-sparsity priors with automatic differentiation

Sparsity priors are commonly used in denoising and image reconstruction. For analysis-type priors, a dictionary defines a representation of signals that is likely to be sparse. In most situations, this dictionary is not known, and is to be recovered from pairs of ground-truth signals and measurements, by minimizing the reconstruction error. This defines a hierarchical optimization problem, which can be cast as a bi-level optimization. Yet, this problem is unsolvable, as reconstructions and their derivative wrt the dictionary have no closed-form expression. However, reconstructions can be iteratively computed using the Forward-Backward splitting (FB) algorithm. In this paper, we approximate reconstructions by the output of the aforementioned FB algorithm. Then, we leverage automatic differentiation to evaluate the gradient of this output wrt the dictionary, which we learn with projected gradient descent. Experiments show that our algorithm successfully learns the 1D Total Variation (TV) dictionary from piecewise constant signals. For the same case study, we propose to constrain our search to dictionaries of 0-centered columns, which removes undesired local minima and improves numerical stability.

On the Universality of Graph Neural Networks on Large Random Graphs

We study the approximation power of Graph Neural Networks (GNNs) on latent position random graphs. In the large graph limit, GNNs are known to converge to certain "continuous" models known as c-GNNs, which directly enables a study of their approximation power on random graph models. In the absence of input node features however, just as GNNs are limited by the Weisfeiler-Lehman isomorphism test, c-GNNs will be severely limited on simple random graph models. For instance, they will fail to distinguish the communities of a well-separated Stochastic Block Model (SBM) with constant degree function. Thus, we consider recently proposed architectures that augment GNNs with unique node identifiers, referred to as Structural GNNs here (SGNNs). We study the convergence of SGNNs to their continuous counterpart (c-SGNNs) in the large random graph limit, under new conditions on the node identifiers. We then show that c-SGNNs are strictly more powerful than c-GNNs in the continuous limit, and prove their universality on several random graph models of interest, including most SBMs and a large class of random geometric graphs. Our results cover both permutation-invariant and permutation-equivariant architectures.