Signal processing after quadratic random sketching with optical units

Random data sketching (or projection) is now a classical technique enabling, for instance, approximate numerical linear algebra and machine learning algorithms with reduced computational complexity and memory. In this context, the possibility of performing data processing (such as pattern detection or classification) directly in the sketched domain without accessing the original data was previously achieved for linear random sketching methods and compressive sensing. In this work, we show how to estimate simple signal processing tasks (such as deducing local variations in a image) directly using random quadratic projections achieved by an optical processing unit. The same approach allows for naive data classification methods directly operated in the sketched domain. We report several experiments confirming the power of our approach.

Signal processing with optical quadratic random sketches

Random data sketching (or projection) is now a classical technique enabling, for instance, approximate numerical linear algebra and machine learning algorithms with reduced computational complexity and memory. In this context, the possibility of performing data processing (such as pattern detection or classification) directly in the sketched domain without accessing the original data was previously achieved for linear random sketching methods and compressive sensing. In this work, we show how to estimate simple signal processing tasks (such as deducing local variations in a image) directly using random quadratic projections achieved by an optical processing unit. The same approach allows for naive data classification methods directly operated in the sketched domain. We report several experiments confirming the power of our approach.

M$^2$M: A general method to perform various data analysis tasks from a differentially private sketch

Differential privacy is the standard privacy definition for performing analyses over sensitive data. Yet, its privacy budget bounds the number of tasks an analyst can perform with reasonable accuracy, which makes it challenging to deploy in practice. This can be alleviated by private sketching, where the dataset is compressed into a single noisy sketch vector which can be shared with the analysts and used to perform arbitrarily many analyses. However, the algorithms to perform specific tasks from sketches must be developed on a case-by-case basis, which is a major impediment to their use. In this paper, we introduce the generic moment-to-moment (M$^2$M) method to perform a wide range of data exploration tasks from a single private sketch. Among other things, this method can be used to estimate empirical moments of attributes, the covariance matrix, counting queries (including histograms), and regression models. Our method treats the sketching mechanism as a black-box operation, and can thus be applied to a wide variety of sketches from the literature, widening their ranges of applications without further engineering or privacy loss, and removing some of the technical barriers to the wider adoption of sketches for data exploration under differential privacy. We validate our method with data exploration tasks on artificial and real-world data, and show that it can be used to reliably estimate statistics and train classification models from private sketches.

ROP inception: signal estimation with quadratic random sketching

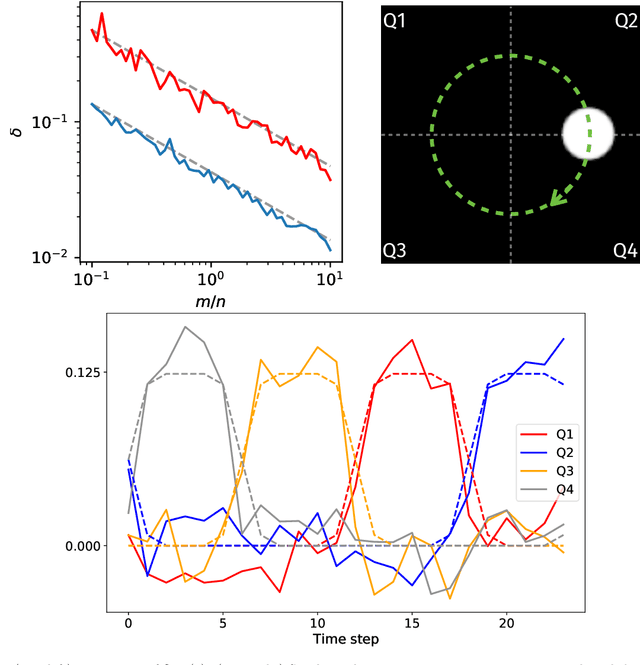
Rank-one projections (ROP) of matrices and quadratic random sketching of signals support several data processing and machine learning methods, as well as recent imaging applications, such as phase retrieval or optical processing units. In this paper, we demonstrate how signal estimation can be operated directly through such quadratic sketches--equivalent to the ROPs of the "lifted signal" obtained as its outer product with itself--without explicitly reconstructing that signal. Our analysis relies on showing that, up to a minor debiasing trick, the ROP measurement operator satisfies a generalised sign product embedding (SPE) property. In a nutshell, the SPE shows that the scalar product of a signal sketch with the "sign" of the sketch of a given pattern approximates the square of the projection of that signal on this pattern. This thus amounts to an insertion (an "inception") of a ROP model inside a ROP sketch. The effectiveness of our approach is evaluated in several synthetic experiments.

Asymmetric compressive learning guarantees with applications to quantized sketches

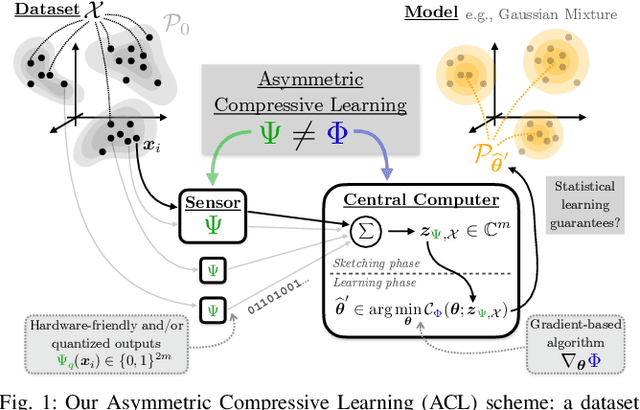
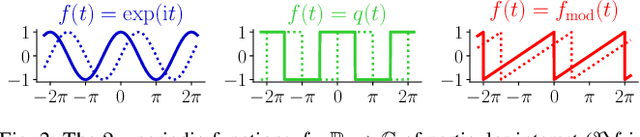
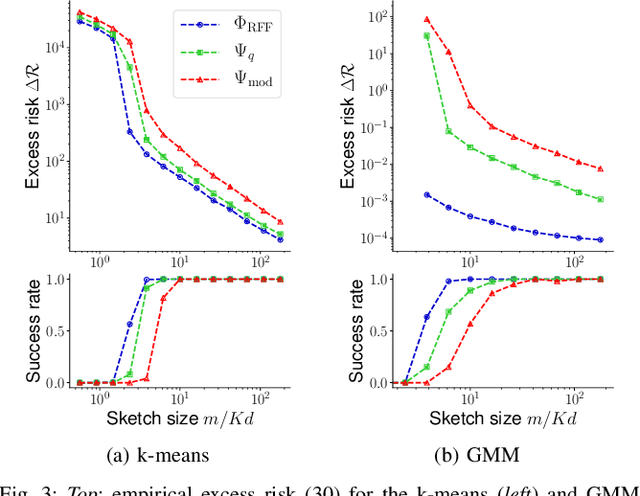
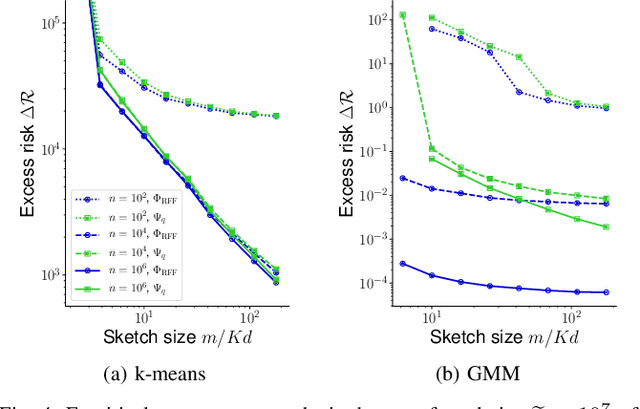
The compressive learning framework reduces the computational cost of training on large-scale datasets. In a sketching phase, the data is first compressed to a lightweight sketch vector, obtained by mapping the data samples through a well-chosen feature map, and averaging those contributions. In a learning phase, the desired model parameters are then extracted from this sketch by solving an optimization problem, which also involves a feature map. When the feature map is identical during the sketching and learning phases, formal statistical guarantees (excess risk bounds) have been proven. However, the desirable properties of the feature map are different during sketching and learning (e.g. quantized outputs, and differentiability, respectively). We thus study the relaxation where this map is allowed to be different for each phase. First, we prove that the existing guarantees carry over to this asymmetric scheme, up to a controlled error term, provided some Limited Projected Distortion (LPD) property holds. We then instantiate this framework to the setting of quantized sketches, by proving that the LPD indeed holds for binary sketch contributions. Finally, we further validate the approach with numerical simulations, including a large-scale application in audio event classification.

When compressive learning fails: blame the decoder or the sketch?

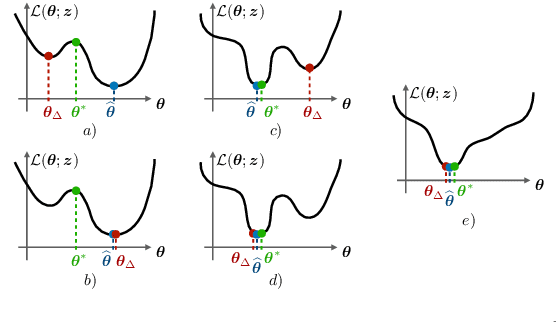
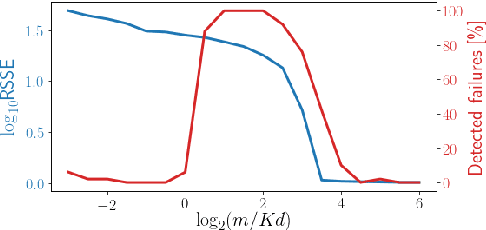
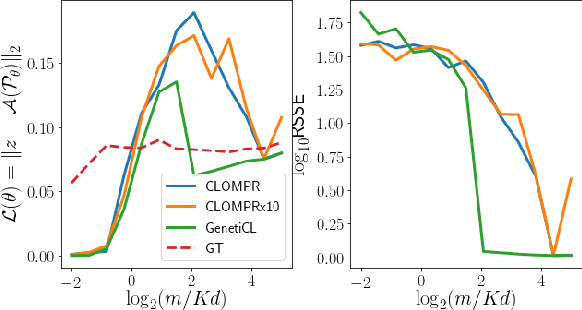
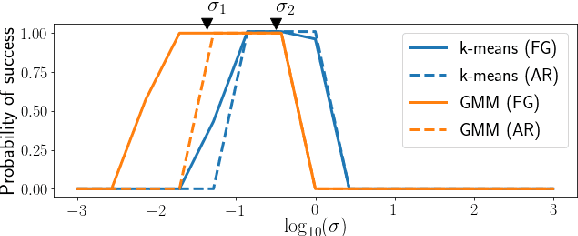
In compressive learning, a mixture model (a set of centroids or a Gaussian mixture) is learned from a sketch vector, that serves as a highly compressed representation of the dataset. This requires solving a non-convex optimization problem, hence in practice approximate heuristics (such as CLOMPR) are used. In this work we explore, by numerical simulations, properties of this non-convex optimization landscape and those heuristics.

Sketching Datasets for Large-Scale Learning (long version)

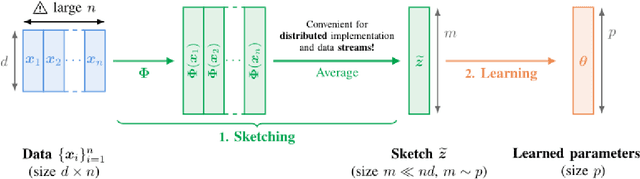
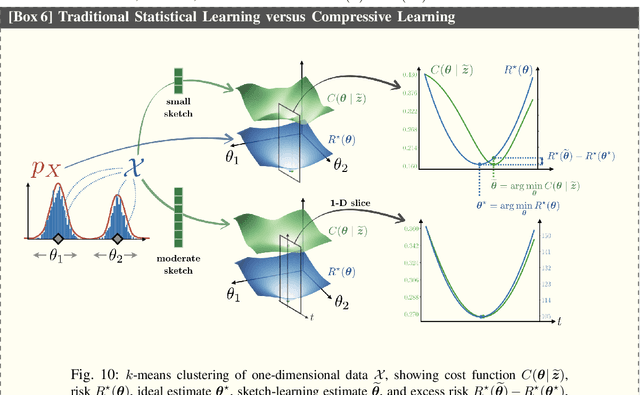
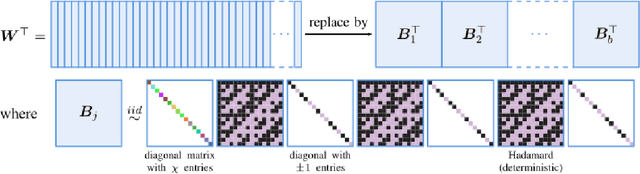
This article considers "sketched learning," or "compressive learning," an approach to large-scale machine learning where datasets are massively compressed before learning (e.g., clustering, classification, or regression) is performed. In particular, a "sketch" is first constructed by computing carefully chosen nonlinear random features (e.g., random Fourier features) and averaging them over the whole dataset. Parameters are then learned from the sketch, without access to the original dataset. This article surveys the current state-of-the-art in sketched learning, including the main concepts and algorithms, their connections with established signal-processing methods, existing theoretical guarantees---on both information preservation and privacy preservation, and important open problems.

Breaking the waves: asymmetric random periodic features for low-bitrate kernel machines

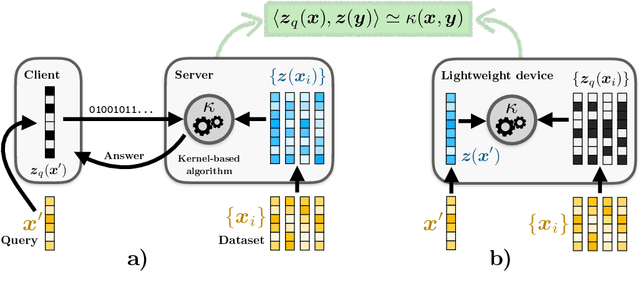
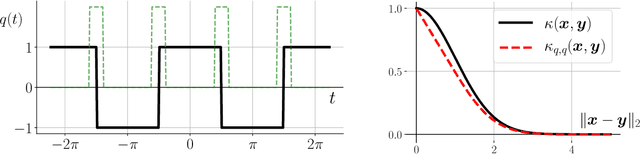
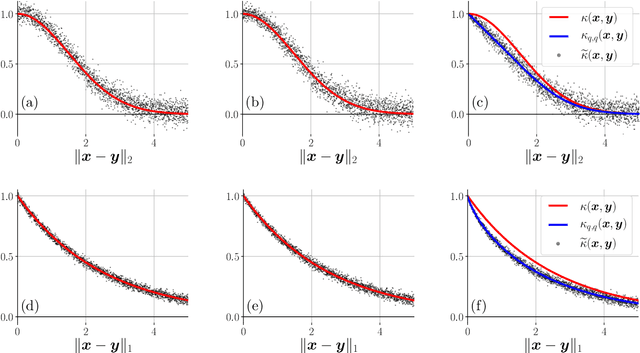
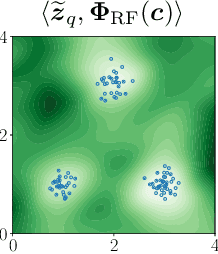
Many signal processing and machine learning applications are built from evaluating a kernel on pairs of signals, e.g. to assess the similarity of an incoming query to a database of known signals. This nonlinear evaluation can be simplified to a linear inner product of the random Fourier features of those signals: random projections followed by a periodic map, the complex exponential. It is known that a simple quantization of those features (corresponding to replacing the complex exponential by a different periodic map that takes binary values, which is appealing for their transmission and storage), distorts the approximated kernel, which may be undesirable in practice. Our take-home message is that when the features of only one of the two signals are quantized, the original kernel is recovered without distortion; its practical interest appears in several cases where the kernel evaluations are asymmetric by nature, such as a client-server scheme. Concretely, we introduce the general framework of asymmetric random periodic features, where the two signals of interest are observed through random periodic features: random projections followed by a general periodic map, which is allowed to be different for both signals. We derive the influence of those periodic maps on the approximated kernel, and prove uniform probabilistic error bounds holding for all signal pairs from an infinite low-complexity set. Interestingly, our results allow the periodic maps to be discontinuous, thanks to a new mathematical tool, i.e. the mean Lipschitz continuity. We then apply this generic framework to semi-quantized kernel machines (where only one signal has quantized features and the other has classical random Fourier features), for which we show theoretically that the approximated kernel remains unchanged (with the associated error bound), and confirm the power of the approach with numerical simulations.

Compressive Learning of Generative Networks

Generative networks implicitly approximate complex densities from their sampling with impressive accuracy. However, because of the enormous scale of modern datasets, this training process is often computationally expensive. We cast generative network training into the recent framework of compressive learning: we reduce the computational burden of large-scale datasets by first harshly compressing them in a single pass as a single sketch vector. We then propose a cost function, which approximates the Maximum Mean Discrepancy metric, but requires only this sketch, which makes it time- and memory-efficient to optimize.

Compressive Classification (Machine Learning without learning)

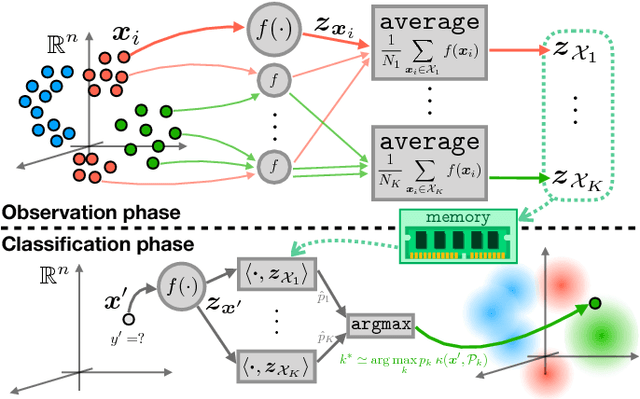
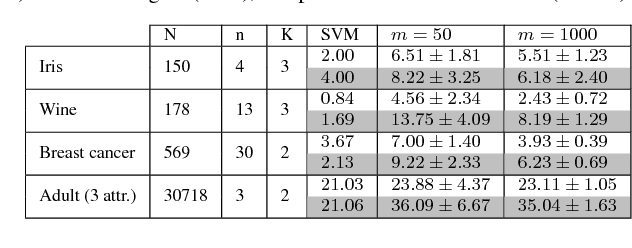
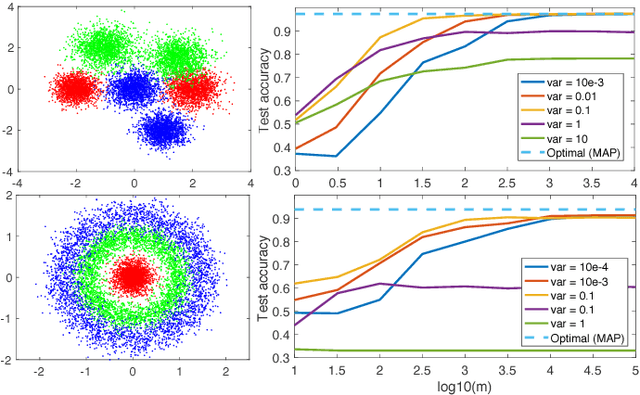
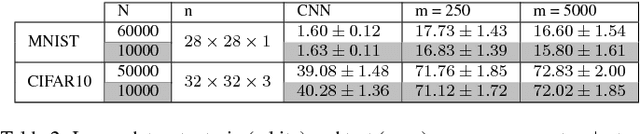
Compressive learning is a framework where (so far unsupervised) learning tasks use not the entire dataset but a compressed summary (sketch) of it. We propose a compressive learning classification method, and a novel sketch function for images.