Optimization Insights into Deep Diagonal Linear Networks

Overparameterized models trained with (stochastic) gradient descent are ubiquitous in modern machine learning. These large models achieve unprecedented performance on test data, but their theoretical understanding is still limited. In this paper, we take a step towards filling this gap by adopting an optimization perspective. More precisely, we study the implicit regularization properties of the gradient flow "algorithm" for estimating the parameters of a deep diagonal neural network. Our main contribution is showing that this gradient flow induces a mirror flow dynamic on the model, meaning that it is biased towards a specific solution of the problem depending on the initialization of the network. Along the way, we prove several properties of the trajectory.

Automatic Gain Tuning for Humanoid Robots Walking Architectures Using Gradient-Free Optimization Techniques

Developing sophisticated control architectures has endowed robots, particularly humanoid robots, with numerous capabilities. However, tuning these architectures remains a challenging and time-consuming task that requires expert intervention. In this work, we propose a methodology to automatically tune the gains of all layers of a hierarchical control architecture for walking humanoids. We tested our methodology by employing different gradient-free optimization methods: Genetic Algorithm (GA), Covariance Matrix Adaptation Evolution Strategy (CMA-ES), Evolution Strategy (ES), and Differential Evolution (DE). We validated the parameter found both in simulation and on the real ergoCub humanoid robot. Our results show that GA achieves the fastest convergence (10 x 10^3 function evaluations vs 25 x 10^3 needed by the other algorithms) and 100% success rate in completing the task both in simulation and when transferred on the real robotic platform. These findings highlight the potential of our proposed method to automate the tuning process, reducing the need for manual intervention.

Linear quadratic control of nonlinear systems with Koopman operator learning and the Nyström method

In this paper, we study how the Koopman operator framework can be combined with kernel methods to effectively control nonlinear dynamical systems. While kernel methods have typically large computational requirements, we show how random subspaces (Nystr\"om approximation) can be used to achieve huge computational savings while preserving accuracy. Our main technical contribution is deriving theoretical guarantees on the effect of the Nystr\"om approximation. More precisely, we study the linear quadratic regulator problem, showing that both the approximated Riccati operator and the regulator objective, for the associated solution of the optimal control problem, converge at the rate $m^{-1/2}$, where $m$ is the random subspace size. Theoretical findings are complemented by numerical experiments corroborating our results.

Stochastic Zeroth order Descent with Structured Directions

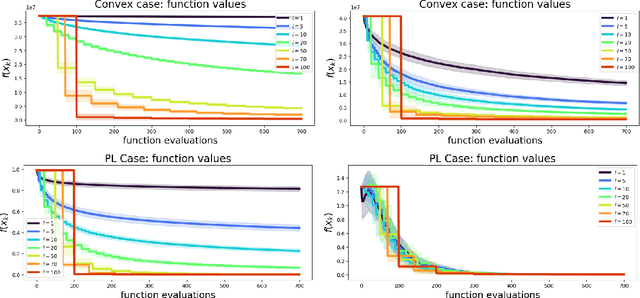
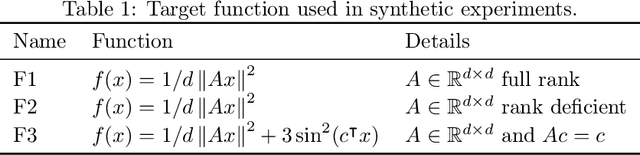
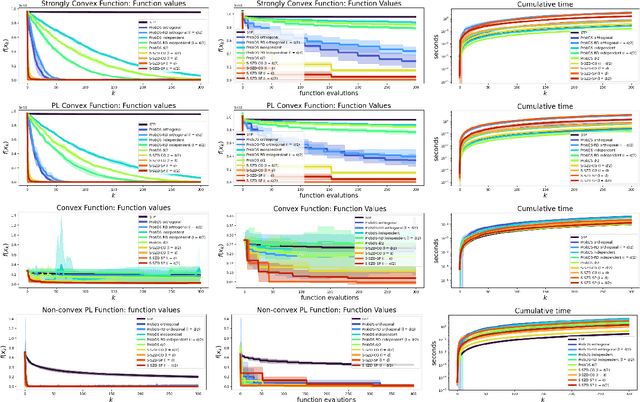
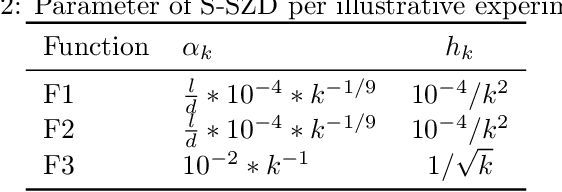
We introduce and analyze Structured Stochastic Zeroth order Descent (S-SZD), a finite difference approach which approximates a stochastic gradient on a set of $l\leq d$ orthogonal directions, where $d$ is the dimension of the ambient space. These directions are randomly chosen, and may change at each step. For smooth convex functions we prove almost sure convergence of the iterates and a convergence rate on the function values of the form $O(d/l k^{-c})$ for every $c<1/2$, which is arbitrarily close to the one of Stochastic Gradient Descent (SGD) in terms of number of iterations. Our bound also shows the benefits of using $l$ multiple directions instead of one. For non-convex functions satisfying the Polyak-{\L}ojasiewicz condition, we establish the first convergence rates for stochastic zeroth order algorithms under such an assumption. We corroborate our theoretical findings in numerical simulations where assumptions are satisfied and on the real-world problem of hyper-parameter optimization, observing that S-SZD has very good practical performances.

Iterative regularization for low complexity regularizers

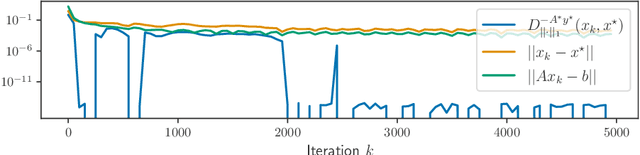
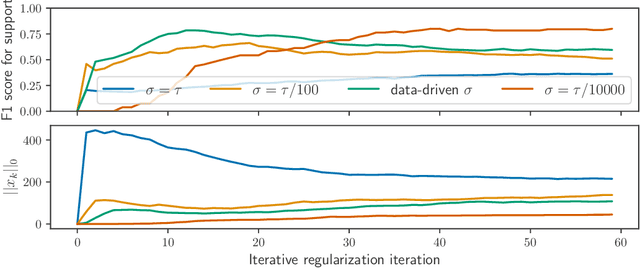
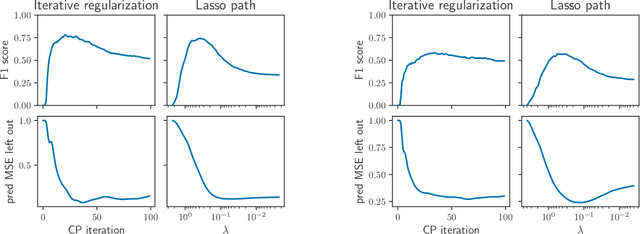
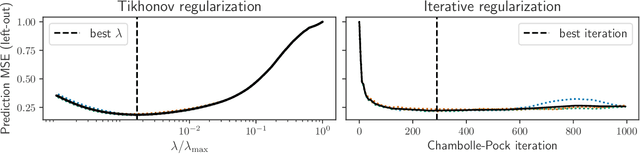
Iterative regularization exploits the implicit bias of an optimization algorithm to regularize ill-posed problems. Constructing algorithms with such built-in regularization mechanisms is a classic challenge in inverse problems but also in modern machine learning, where it provides both a new perspective on algorithms analysis, and significant speed-ups compared to explicit regularization. In this work, we propose and study the first iterative regularization procedure able to handle biases described by non smooth and non strongly convex functionals, prominent in low-complexity regularization. Our approach is based on a primal-dual algorithm of which we analyze convergence and stability properties, even in the case where the original problem is unfeasible. The general results are illustrated considering the special case of sparse recovery with the $\ell_1$ penalty. Our theoretical results are complemented by experiments showing the computational benefits of our approach.

A Stochastic Bregman Primal-Dual Splitting Algorithm for Composite Optimization

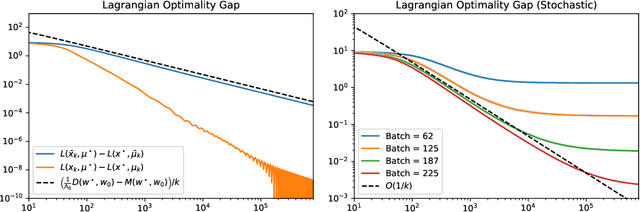
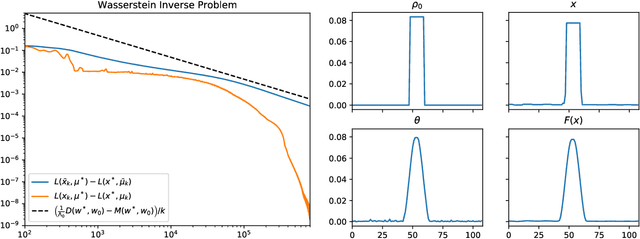
We study a stochastic first order primal-dual method for solving convex-concave saddle point problems over real reflexive Banach spaces using Bregman divergences and relative smoothness assumptions, in which we allow for stochastic error in the computation of gradient terms within the algorithm. We show ergodic convergence in expectation of the Lagrangian optimality gap with a rate of O(1/k) and that every almost sure weak cluster point of the ergodic sequence is a saddle point in expectation under mild assumptions. Under slightly stricter assumptions, we show almost sure weak convergence of the pointwise iterates to a saddle point. Under a relative strong convexity assumption on the objective functions and a total convexity assumption on the entropies of the Bregman divergences, we establish almost sure strong convergence of the pointwise iterates to a saddle point. Our framework is general and does not need strong convexity of the entropies inducing the Bregman divergences in the algorithm. Numerical applications are considered including entropically regularized Wasserstein barycenter problems and regularized inverse problems on the simplex.

Implicit regularization for convex regularizers

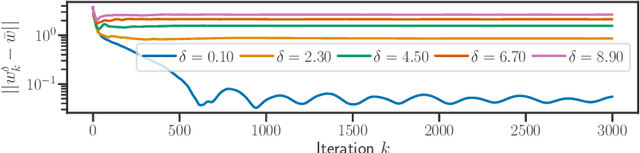
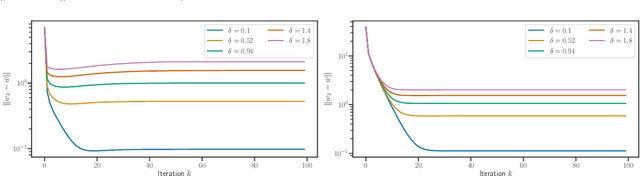
We study implicit regularization for over-parameterized linear models, when the bias is convex but not necessarily strongly convex. We characterize the regularization property of a primal-dual gradient based approach, analyzing convergence and especially stability in the presence of worst case deterministic noise. As a main example, we specialize and illustrate the results for the problem of robust sparse recovery. Key to our analysis is a combination of ideas from regularization theory and optimization in the presence of errors. Theoretical results are complemented by experiments showing that state-of-the-art performances are achieved with considerable computational speed-ups.

Inexact and Stochastic Generalized Conditional Gradient with Augmented Lagrangian and Proximal Step

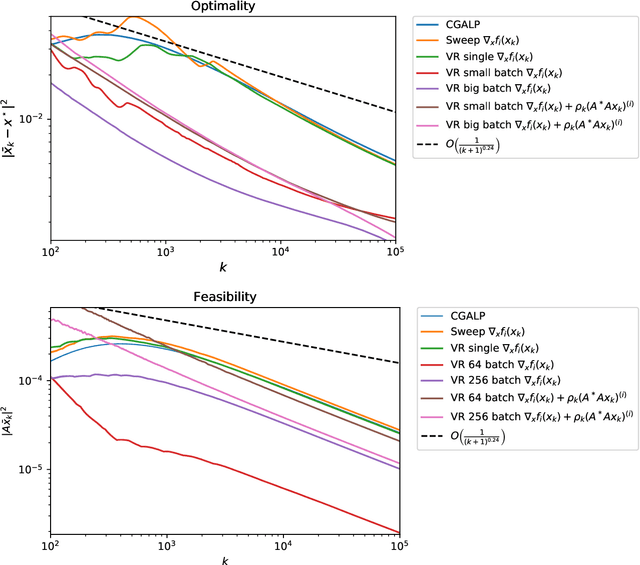
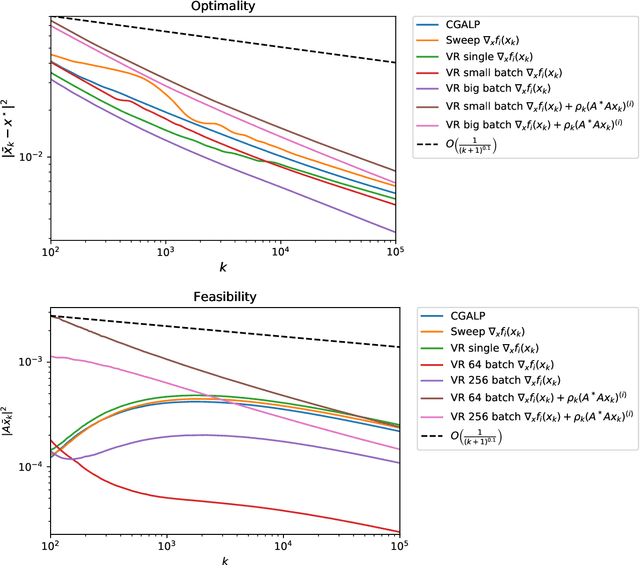
In this paper we propose and analyze inexact and stochastic versions of the CGALP algorithm developed in the authors' previous paper, which we denote ICGALP, that allows for errors in the computation of several important quantities. In particular this allows one to compute some gradients, proximal terms, and/or linear minimization oracles in an inexact fashion that facilitates the practical application of the algorithm to computationally intensive settings, e.g. in high (or possibly infinite) dimensional Hilbert spaces commonly found in machine learning problems. The algorithm is able to solve composite minimization problems involving the sum of three convex proper lower-semicontinuous functions subject to an affine constraint of the form $Ax=b$ for some bounded linear operator $A$. Only one of the functions in the objective is assumed to be differentiable, the other two are assumed to have an accessible prox operator and a linear minimization oracle. As main results, we show convergence of the Lagrangian to an optimum and asymptotic feasibility of the affine constraint as well as weak convergence of the dual variable to a solution of the dual problem, all in an almost sure sense. Almost sure convergence rates, both pointwise and ergodic, are given for the Lagrangian values and the feasibility gap. Numerical experiments verifying the predicted rates of convergence are shown as well.