Towards Differential Relational Privacy and its use in Question Answering

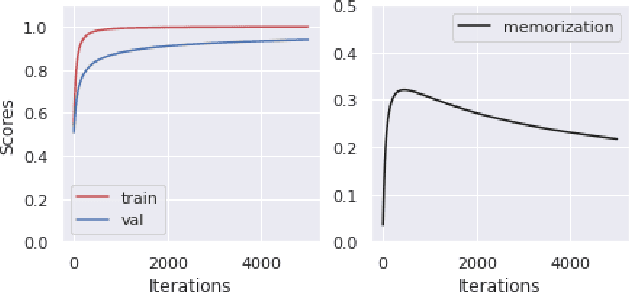
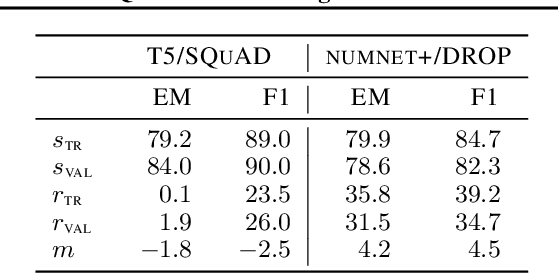
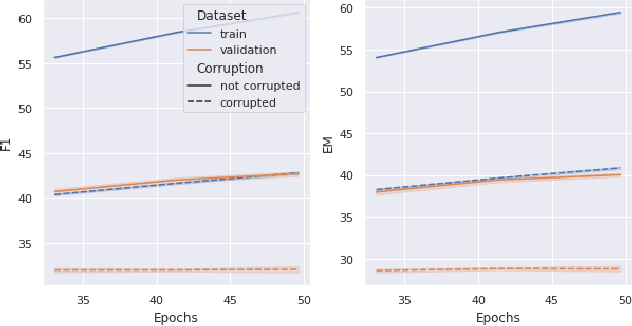
Memorization of the relation between entities in a dataset can lead to privacy issues when using a trained model for question answering. We introduce Relational Memorization (RM) to understand, quantify and control this phenomenon. While bounding general memorization can have detrimental effects on the performance of a trained model, bounding RM does not prevent effective learning. The difference is most pronounced when the data distribution is long-tailed, with many queries having only few training examples: Impeding general memorization prevents effective learning, while impeding only relational memorization still allows learning general properties of the underlying concepts. We formalize the notion of Relational Privacy (RP) and, inspired by Differential Privacy (DP), we provide a possible definition of Differential Relational Privacy (DrP). These notions can be used to describe and compute bounds on the amount of RM in a trained model. We illustrate Relational Privacy concepts in experiments with large-scale models for Question Answering.

Mixed Differential Privacy in Computer Vision

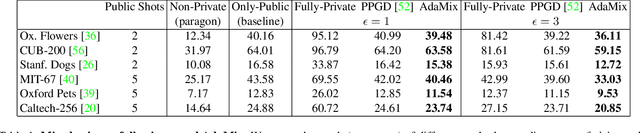
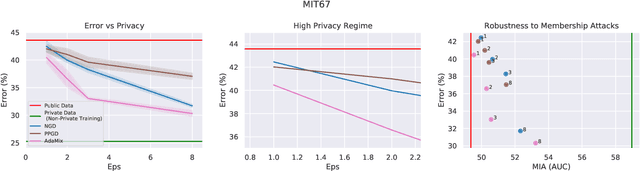
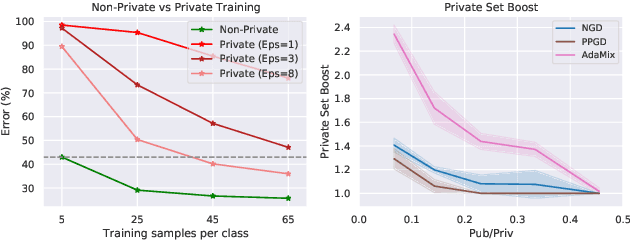
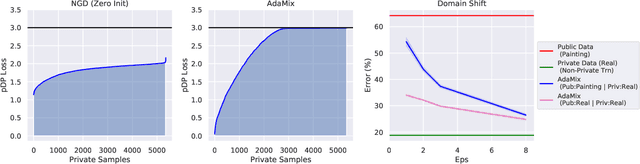
We introduce AdaMix, an adaptive differentially private algorithm for training deep neural network classifiers using both private and public image data. While pre-training language models on large public datasets has enabled strong differential privacy (DP) guarantees with minor loss of accuracy, a similar practice yields punishing trade-offs in vision tasks. A few-shot or even zero-shot learning baseline that ignores private data can outperform fine-tuning on a large private dataset. AdaMix incorporates few-shot training, or cross-modal zero-shot learning, on public data prior to private fine-tuning, to improve the trade-off. AdaMix reduces the error increase from the non-private upper bound from the 167-311\% of the baseline, on average across 6 datasets, to 68-92\% depending on the desired privacy level selected by the user. AdaMix tackles the trade-off arising in visual classification, whereby the most privacy sensitive data, corresponding to isolated points in representation space, are also critical for high classification accuracy. In addition, AdaMix comes with strong theoretical privacy guarantees and convergence analysis.

DIVA: Dataset Derivative of a Learning Task

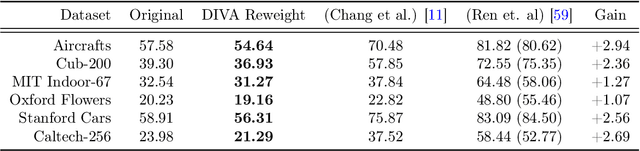
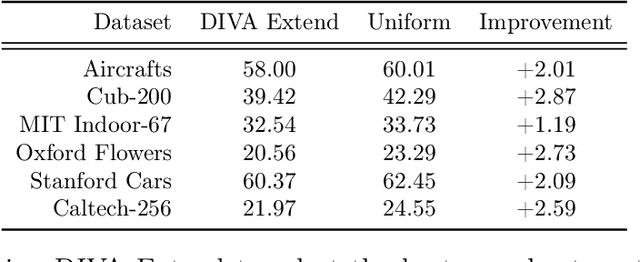
We present a method to compute the derivative of a learning task with respect to a dataset. A learning task is a function from a training set to the validation error, which can be represented by a trained deep neural network (DNN). The "dataset derivative" is a linear operator, computed around the trained model, that informs how perturbations of the weight of each training sample affect the validation error, usually computed on a separate validation dataset. Our method, DIVA (Differentiable Validation) hinges on a closed-form differentiable expression of the leave-one-out cross-validation error around a pre-trained DNN. Such expression constitutes the dataset derivative. DIVA could be used for dataset auto-curation, for example removing samples with faulty annotations, augmenting a dataset with additional relevant samples, or rebalancing. More generally, DIVA can be used to optimize the dataset, along with the parameters of the model, as part of the training process without the need for a separate validation dataset, unlike bi-level optimization methods customary in AutoML. To illustrate the flexibility of DIVA, we report experiments on sample auto-curation tasks such as outlier rejection, dataset extension, and automatic aggregation of multi-modal data.

A linearized framework and a new benchmark for model selection for fine-tuning

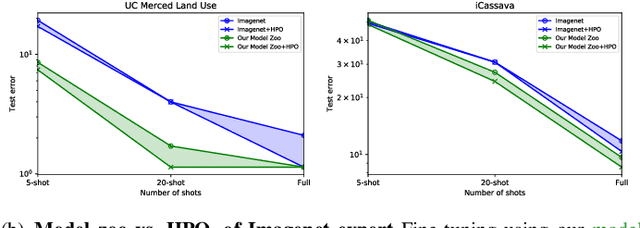
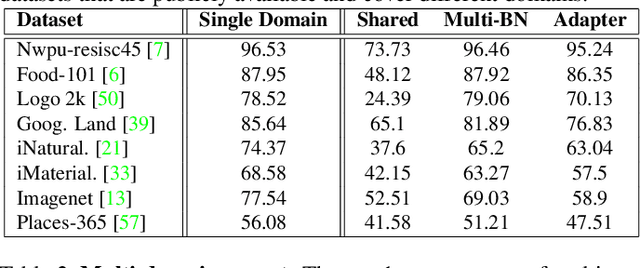
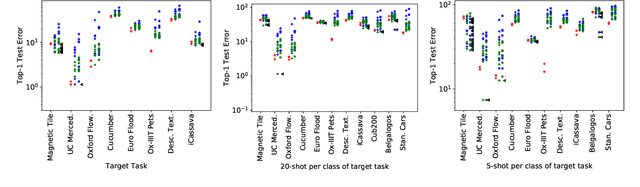
Fine-tuning from a collection of models pre-trained on different domains (a "model zoo") is emerging as a technique to improve test accuracy in the low-data regime. However, model selection, i.e. how to pre-select the right model to fine-tune from a model zoo without performing any training, remains an open topic. We use a linearized framework to approximate fine-tuning, and introduce two new baselines for model selection -- Label-Gradient and Label-Feature Correlation. Since all model selection algorithms in the literature have been tested on different use-cases and never compared directly, we introduce a new comprehensive benchmark for model selection comprising of: i) A model zoo of single and multi-domain models, and ii) Many target tasks. Our benchmark highlights accuracy gain with model zoo compared to fine-tuning Imagenet models. We show our model selection baseline can select optimal models to fine-tune in few selections and has the highest ranking correlation to fine-tuning accuracy compared to existing algorithms.

Structured Prediction as Translation between Augmented Natural Languages

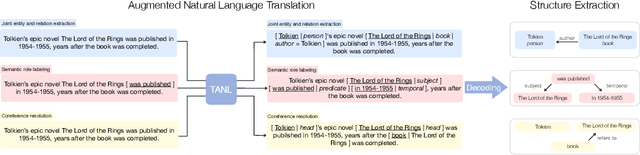
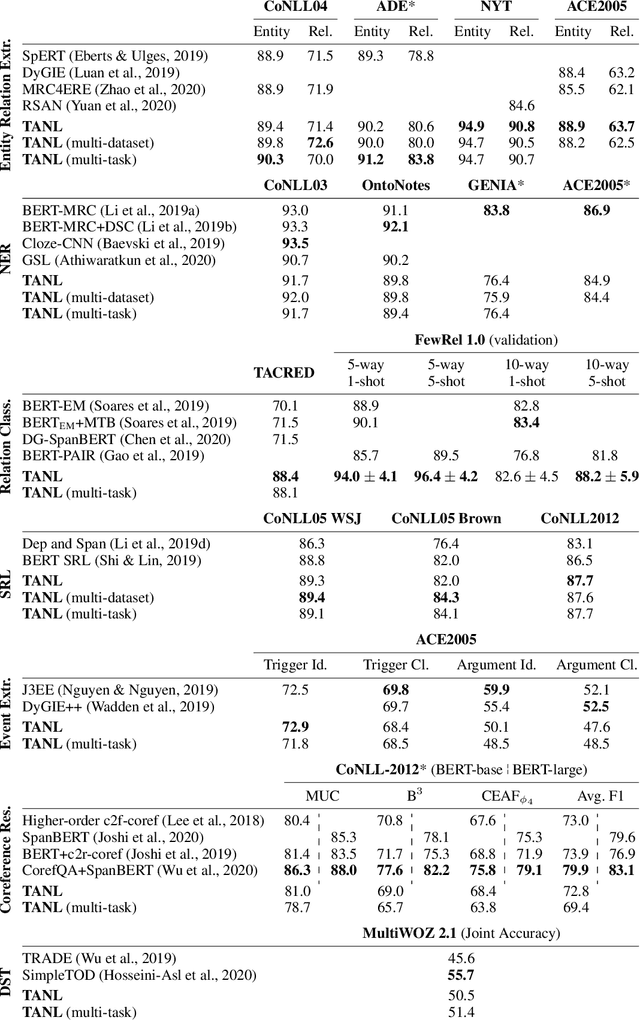
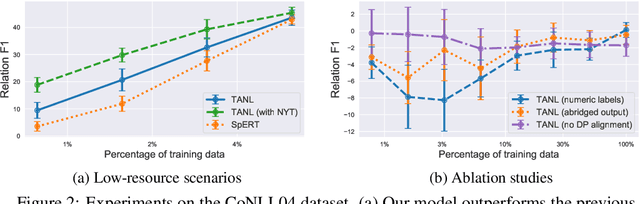
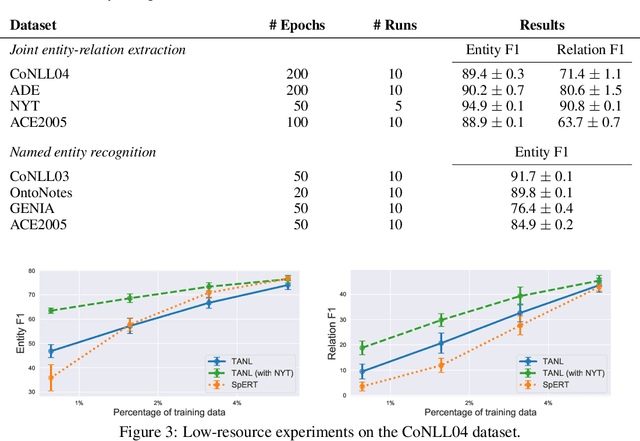
We propose a new framework, Translation between Augmented Natural Languages (TANL), to solve many structured prediction language tasks including joint entity and relation extraction, nested named entity recognition, relation classification, semantic role labeling, event extraction, coreference resolution, and dialogue state tracking. Instead of tackling the problem by training task-specific discriminative classifiers, we frame it as a translation task between augmented natural languages, from which the task-relevant information can be easily extracted. Our approach can match or outperform task-specific models on all tasks, and in particular, achieves new state-of-the-art results on joint entity and relation extraction (CoNLL04, ADE, NYT, and ACE2005 datasets), relation classification (FewRel and TACRED), and semantic role labeling (CoNLL-2005 and CoNLL-2012). We accomplish this while using the same architecture and hyperparameters for all tasks and even when training a single model to solve all tasks at the same time (multi-task learning). Finally, we show that our framework can also significantly improve the performance in a low-resource regime, thanks to better use of label semantics.

Estimating informativeness of samples with Smooth Unique Information

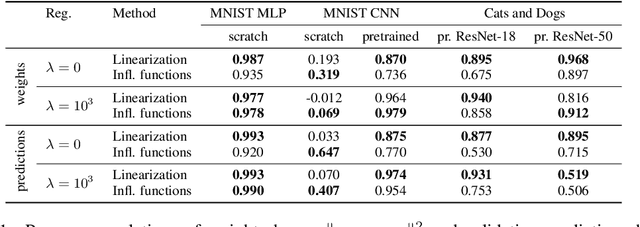
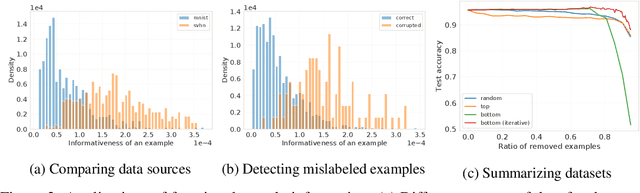
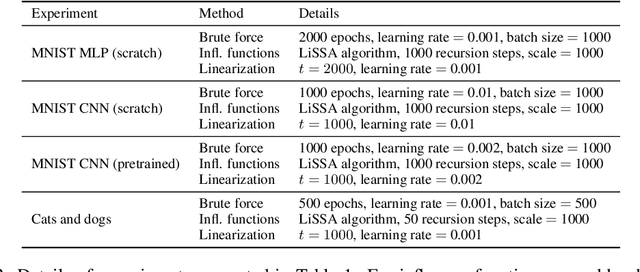
We define a notion of information that an individual sample provides to the training of a neural network, and we specialize it to measure both how much a sample informs the final weights and how much it informs the function computed by the weights. Though related, we show that these quantities have a qualitatively different behavior. We give efficient approximations of these quantities using a linearized network and demonstrate empirically that the approximation is accurate for real-world architectures, such as pre-trained ResNets. We apply these measures to several problems, such as dataset summarization, analysis of under-sampled classes, comparison of informativeness of different data sources, and detection of adversarial and corrupted examples. Our work generalizes existing frameworks but enjoys better computational properties for heavily over-parametrized models, which makes it possible to apply it to real-world networks.

Mixed-Privacy Forgetting in Deep Networks

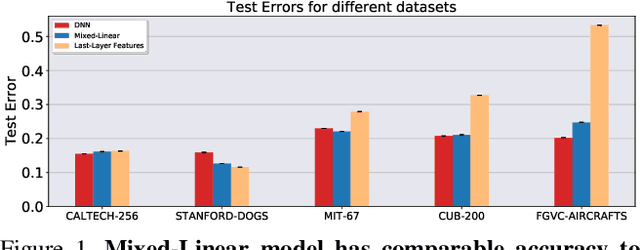
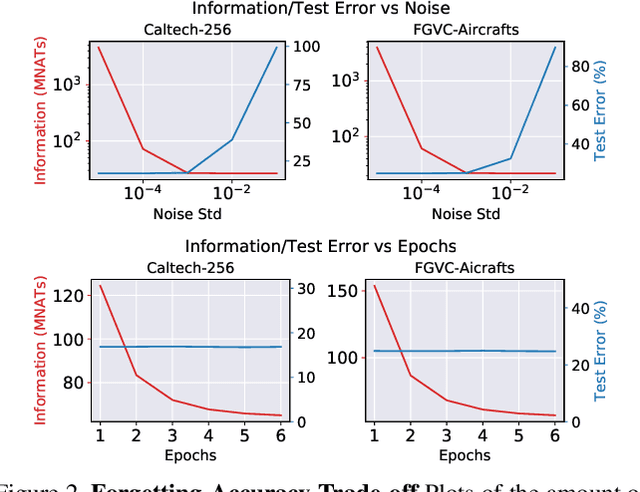
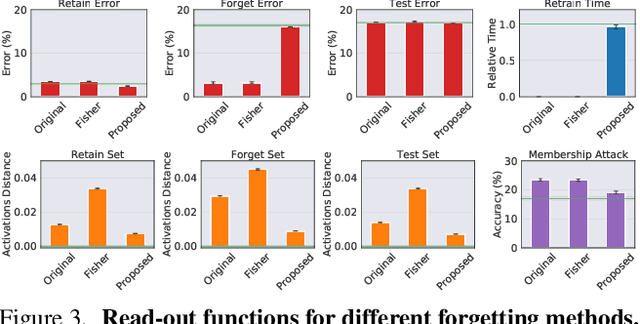
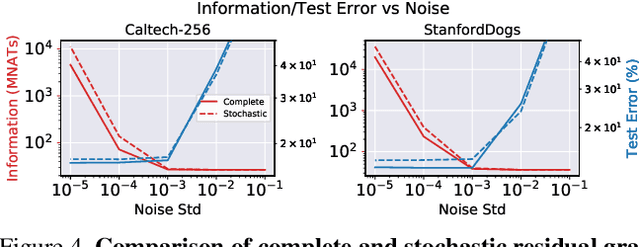
We show that the influence of a subset of the training samples can be removed -- or "forgotten" -- from the weights of a network trained on large-scale image classification tasks, and we provide strong computable bounds on the amount of remaining information after forgetting. Inspired by real-world applications of forgetting techniques, we introduce a novel notion of forgetting in mixed-privacy setting, where we know that a "core" subset of the training samples does not need to be forgotten. While this variation of the problem is conceptually simple, we show that working in this setting significantly improves the accuracy and guarantees of forgetting methods applied to vision classification tasks. Moreover, our method allows efficient removal of all information contained in non-core data by simply setting to zero a subset of the weights with minimal loss in performance. We achieve these results by replacing a standard deep network with a suitable linear approximation. With opportune changes to the network architecture and training procedure, we show that such linear approximation achieves comparable performance to the original network and that the forgetting problem becomes quadratic and can be solved efficiently even for large models. Unlike previous forgetting methods on deep networks, ours can achieve close to the state-of-the-art accuracy on large scale vision tasks. In particular, we show that our method allows forgetting without having to trade off the model accuracy.

LQF: Linear Quadratic Fine-Tuning

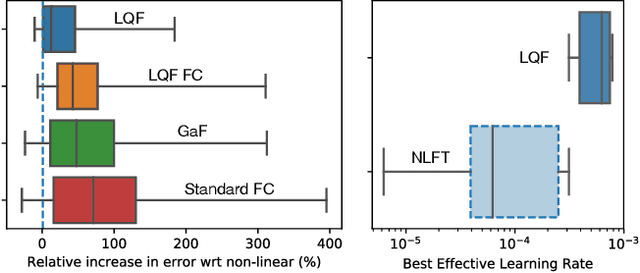
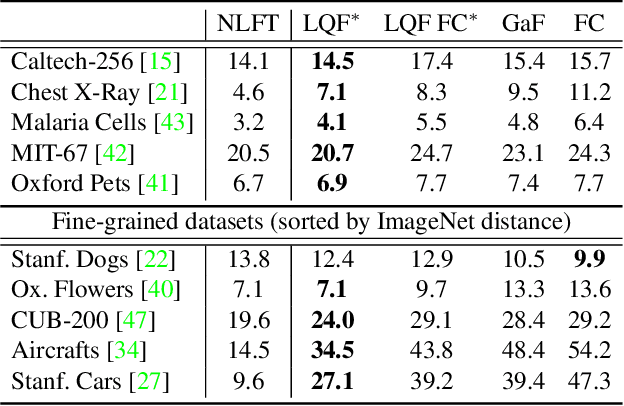
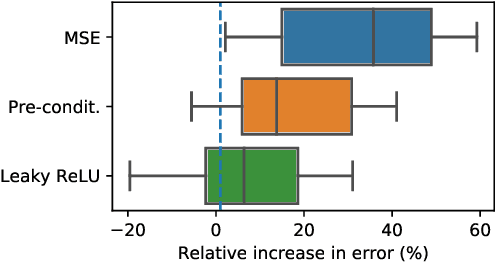
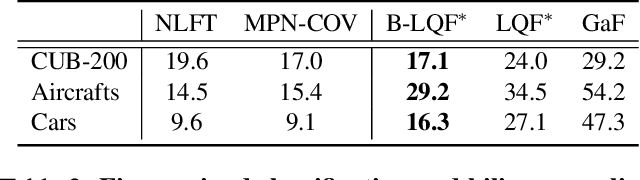
Classifiers that are linear in their parameters, and trained by optimizing a convex loss function, have predictable behavior with respect to changes in the training data, initial conditions, and optimization. Such desirable properties are absent in deep neural networks (DNNs), typically trained by non-linear fine-tuning of a pre-trained model. Previous attempts to linearize DNNs have led to interesting theoretical insights, but have not impacted the practice due to the substantial performance gap compared to standard non-linear optimization. We present the first method for linearizing a pre-trained model that achieves comparable performance to non-linear fine-tuning on most of real-world image classification tasks tested, thus enjoying the interpretability of linear models without incurring punishing losses in performance. LQF consists of simple modifications to the architecture, loss function and optimization typically used for classification: Leaky-ReLU instead of ReLU, mean squared loss instead of cross-entropy, and pre-conditioning using Kronecker factorization. None of these changes in isolation is sufficient to approach the performance of non-linear fine-tuning. When used in combination, they allow us to reach comparable performance, and even superior in the low-data regime, while enjoying the simplicity, robustness and interpretability of linear-quadratic optimization.

Usable Information and Evolution of Optimal Representations During Training

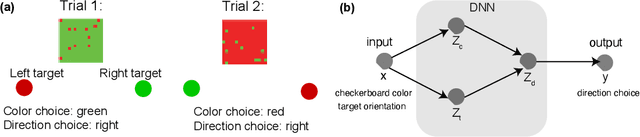
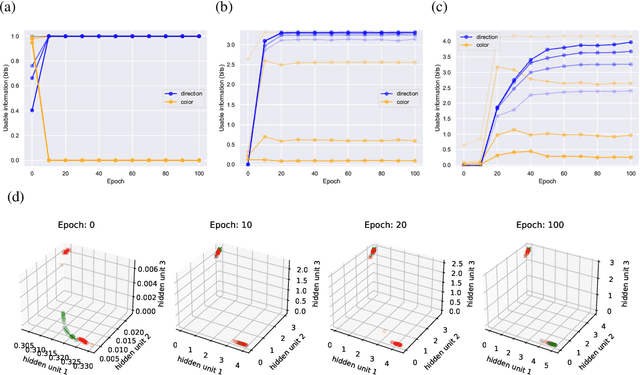
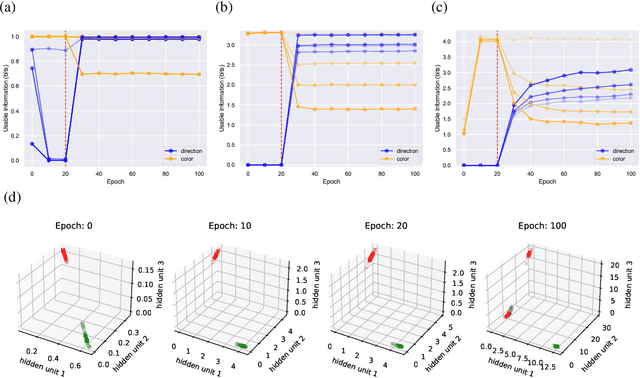
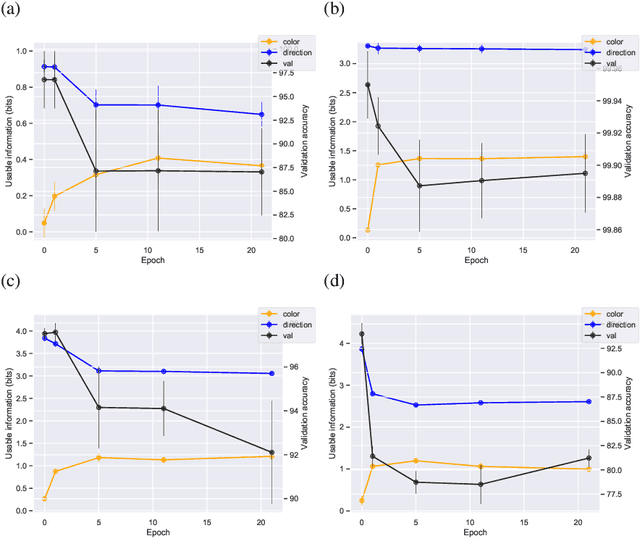
We introduce a notion of usable information contained in the representation learned by a deep network, and use it to study how optimal representations for the task emerge during training, and how they adapt to different tasks. We use this to characterize the transient dynamics of deep neural networks on perceptual decision-making tasks inspired by neuroscience literature. In particular, we show that both the random initialization and the implicit regularization from Stochastic Gradient Descent play an important role in learning minimal sufficient representations for the task. If the network is not randomly initialized, we show that the training may not recover an optimal representation, increasing the chance of overfitting.

Predicting Training Time Without Training

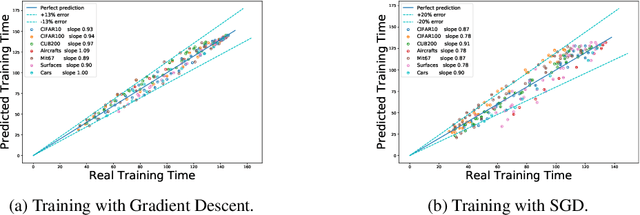
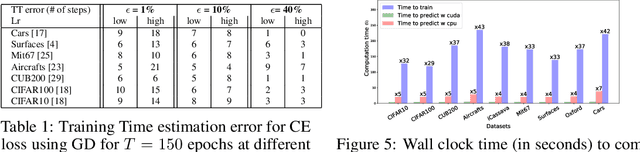
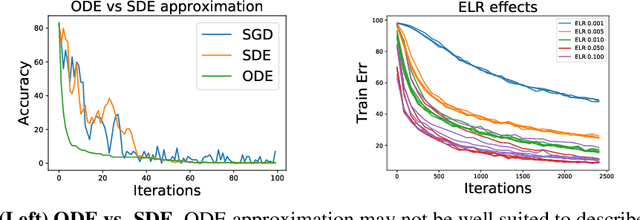
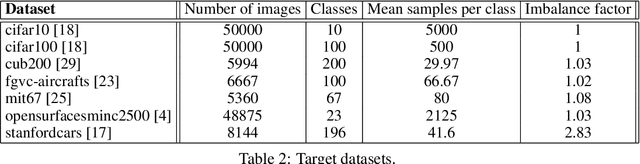
We tackle the problem of predicting the number of optimization steps that a pre-trained deep network needs to converge to a given value of the loss function. To do so, we leverage the fact that the training dynamics of a deep network during fine-tuning are well approximated by those of a linearized model. This allows us to approximate the training loss and accuracy at any point during training by solving a low-dimensional Stochastic Differential Equation (SDE) in function space. Using this result, we are able to predict the time it takes for Stochastic Gradient Descent (SGD) to fine-tune a model to a given loss without having to perform any training. In our experiments, we are able to predict training time of a ResNet within a 20% error margin on a variety of datasets and hyper-parameters, at a 30 to 45-fold reduction in cost compared to actual training. We also discuss how to further reduce the computational and memory cost of our method, and in particular we show that by exploiting the spectral properties of the gradients' matrix it is possible predict training time on a large dataset while processing only a subset of the samples.